重走长征路---OI每周刷题记录---11月4日 2013
总目录详见https://blog.csdn.net/mrcrack/article/details/84471041
做题原则,找不到测评地址的题不做。2018-11-28
重走长征路---OI每周刷题记录---11月4日 2013
本周共计22题
吐槽一下,该周不仅题目多,且不易。2019-1-29 07:55
测评地址:
dp
1.免费馅饼 //在线测评地址http://218.5.5.242:9018/JudgeOnline/problem.php?id=1142
2.石子合并 //在线测评地址https://www.luogu.org/problemnew/show/P1880
3.拦截导弹 //在线测评地址http://218.5.5.242:9018/JudgeOnline/problem.php?id=1407
4.能量项链 //在线测评地址https://www.luogu.org/problemnew/show/P1063
5.找雷 //在线测评地址https://www.luogu.org/problemnew/show/P2196
并查集
6.亲戚 //在线测评地址http://codevs.cn/problem/1073/
贪心
7.观光公交
heap
8.合并果子 //在线测评地址https://www.luogu.org/problemnew/show/P1090
模拟
9.寻宝 //在线测评地址https://www.luogu.org/problemnew/show/P1076
hash
10.方程的解数 //在线测评地址http://codevs.cn/problem/1735/
数论
11.数列 //在线测评地址https://www.luogu.org/problemnew/show/P1062
12.同余方程 //在线测评地址https://www.luogu.org/problemnew/show/P1082
13.多项式系数 //在线测评地址https://www.luogu.org/problemnew/show/P1313
dfs
14.选数 //在线测评地址https://www.luogu.org/problemnew/show/P1036
高精度
15.回文数 //在线测评地址https://www.luogu.org/problemnew/show/P1015
模拟
16.现在几点钟 //在线测评地址http://218.5.5.242:9018/JudgeOnline/problem.php?id=1063
17.选择客栈 //在线测评地址https://www.luogu.org/problemnew/show/P1311
18.机器翻译 //在线测评地址https://www.luogu.org/problemnew/show/P1540
19.计算器的改良 //在线测评地址https://www.luogu.org/problemnew/show/P1022
20.分数线划定 //在线测评地址https://www.luogu.org/problemnew/show/P1068
进制
21.进制转换 //在线测评地址https://www.luogu.org/problemnew/show/P1015
枚举
22.一元三次方程求解 //在线测评地址https://www.luogu.org/problemnew/show/P1024
题解:
dp
1.免费馅饼
//1142: 免费馅饼
//在线测评地址http://218.5.5.242:9018/JudgeOnline/problem.php?id=1142
//看题,没什么思路,查找网络,此文https://blog.csdn.net/sbs2000/article/details/50670773给出思路
//由于馅饼下落的时间和速度都不同,人只能向左右移动,馅饼只能向下移动。人和馅饼都同时移动,思考起来比较复杂,因此我们需要转变思路:
//算出每个时刻落到最底层的每个格子有多少分值的馅饼。
//如果将馅饼当成参照物,则馅饼向下落,可以看成馅饼不动,人往上走去摘取馅饼,这样人每1时刻都可以走到上一行的5个格子,
//这道题是经典动规模型数塔的变形,将馅饼落下的位置看做数塔中的列数,将下落的时间看做数塔中的行数,问题转化为求解从塔底到塔顶的最长路径。
//以上为摘抄内容,开始独立编写。a[i][j]第i秒到达底部的j列的馅饼分数值
//该题考得比较全面,还需记录路径
//切记,编好一部分功能,须及时进行测试。
//分数值应该为非负,该题需进行说明。
//该题可能存在多解,不过题目未作说明,如何处理。
//编好,样例无法通过,
//发现因需记录路径,无需再写max函数了
//样例通过,重新读了代码,发现有冗余代码,删改,
//提交,答案错误33%
//重读题目,发现,时间最大值1000+100/1=1100,故[1100][110]需修改,
//仔细想了想,有一个开始位置,有一个结束位置,开始位置没有考虑,可能不从0开始,开始误以为从0开始
//修改,提交,答案错误50%。
//翻看http://hzwer.com/124.html代码,才发现,有些馅饼竟然可以接不到,真是没想到
//修改,提交,答案错误50%。2019-1-25 21:42
//发现数组a[][]未初始化,初始化后,提交,答案错误50%,2019-1-25 22:32
//突然间想到,既然有些馅饼接不到,那么有些时间段,也可以没有一块馅饼
//故,代码的最大值是没有问题的,问题出在打印路径上。
//打印路径需判定,上一层若无,仔细想了想,这个想法不对
//反复读代码,读题,发现,代码写得有问题,中间时间就算没有馅饼了,人也可以做决策
//begin变量造成该题的问题,时间应该是从0开始的。而非从begin开始。
//修改,提交,答案错误33%。2019-1-25 22:52
//无奈,将http://hzwer.com/124.html代码进行修改,不断靠近自己代码,每改动一点,提交AC,继续改动
//终于发现自己代码问题,b=0;摆错位置,应该是在两重循环之内,而非两重循环之间
//修改,提交AC。2019-1-25 23:29 真不容易啊。
#include
#include
int a[1200][110],W,H,b,p[1200][110];//p[i][j]=k记录路径,a[i][j]来自 a[i+1][k]
int max(int a,int b){
return a>b?a:b;
}
int main(){
int i,j,start,h,d,v,pos,k,end=0;//pos起始位置
scanf("%d%d",&W,&H);
memset(a,0,sizeof(a));//漏了此句
while(scanf("%d%d%d%d",&start,&h,&d,&v)!=EOF){
if((H-1)%d==0){//漏了此举判断
end=max(end,start+(H-1)/d);
a[start+(H-1)/d][h]+=v;
}
}
for(i=end;i>=0;i--){//此处写成for(i=end;i>=begin-1;i--)//此处写成 for(i=t;i>=0;i--)
//b=0;放在此处查了好久,花了2小时
for(j=1;j<=W;j++){
b=0;//添加 ,花了2小时
if(j-2>=1&&b
}
}
pos=(W+1)/2;
printf("%d\n",a[0][pos]);
for(i=0;i
pos=p[i][pos];
}
return 0;
}
2.石子合并
//P1880 [NOI1995]石子合并
//在线测评地址https://www.luogu.org/problemnew/show/P1880
//感觉要区分,顺时针,逆时针,但动笔研究,发现不影响结果
//化圈为线,将N堆石子,变成N+N=2N堆石子即可,这样就可以在数组中直接处理
//先写最大得分。最小得分,照葫芦画瓢即可。
//单个石子的最大值,最小值,没作说明,int是否溢出?
//编到后面,突然发现,弄明白样例是关键
//该题缺一个样例解释啊,突然感觉,样例没弄明白
//4 5 9 4
// 9 9 4 9+
// 18 4 9+18
// 22 9+18+22=49
//
//4 5 9 4
// 9 13 9+13
// 22 9+13+22=44
//大致弄明白了
//突然想到要用前缀和,否则该题极难处理
//样例通过,提交AC。2019-1-26 20:17
#include
#include
int n,a[210],dp1[210][210],dp2[210][210],sum[210];
int min(int a,int b){
return a
int max(int a,int b){
return a>b?a:b;
}
int main(){
int i,j,k,p=999999999,q=-1;//p,q初始化,很重要。
memset(sum,0,sizeof(sum));
scanf("%d",&n);
memset(dp1,127,sizeof(dp1)),memset(dp2,0,sizeof(dp2));
for(i=1;i<=2*n;i++)dp1[i][i]=0;//此行很关键
for(i=1;i<=n;i++)scanf("%d",&a[i]),a[n+i]=a[i];
for(i=1;i<=2*n;i++)sum[i]+=sum[i-1]+a[i];
for(k=1;k
for(j=i;j
dp1[i][i+k]=min(dp1[i][i+k],dp1[i][j]+dp1[j+1][i+k]+sum[i+k]-sum[i-1]);
dp2[i][i+k]=max(dp2[i][i+k],dp2[i][j]+dp2[j+1][i+k]+sum[i+k]-sum[i-1]);//此处写成 dp[i][i+k]=max(dp[i][i+k],dp[i][j]+dp[i+j+1][i+k]);
}
for(i=1;i<=n;i++){
p=min(p,dp1[i][i+n-1]);
q=max(q,dp2[i][i+n-1]);
}
printf("%d\n%d\n",p,q);
return 0;
}
3.拦截导弹
//1407: 拦截导弹
//在线测评地址http://218.5.5.242:9018/JudgeOnline/problem.php?id=1407
//该题的难点在于,n<=100000,O(n^2)算法无法AC
//只能采用O(nlogn)算法
//二分。
//样例通过,提交83%,答案错误,翻看之前的编码https://blog.csdn.net/mrcrack/article/details/84928209
//中的//P1020 导弹拦截
//仔细想想,原来的写法确实有问题,修改,提交AC。2019-1-17 21:02
//原来的写法,极端情况,二分在f[1],f[2]结束
//现在的写法,极端情况,在f[0],f[1]结束。
#include
#define maxn 100100
int f[maxn],ans=0;//f[]是一个递减序列
int main(){
int n,h,i,left,right,mid;
scanf("%d",&n);
f[0]=100100;//飞行高度不高于10^5
for(i=1;i<=n;i++){
scanf("%d",&h);
if(f[ans]>=h)ans++,f[ans]=h;//漏了此句 f[ans]=h
else{
left=0,right=ans;//此处写成left=1//此处left赋值很关键
while(left+1
if(f[mid]
}
f[right]=h;//此处写成f[left]=h;
}
}
printf("%d\n",ans);
return 0;
}
4.能量项链
//P1063 能量项链
//NOIP 2006 提高组 第1题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P1063
//题目对样例解释得清清楚楚,出得好。
//化圈为线,由N个珠子变成2*N个珠子,处理起来就方便了
//题目连数据范围都说得很清楚,真是出得好。
//并且说明了,顺逆时针。试了下
//顺时针
//1 2 3 4 (2,3)(3,5)(5,10)(10,2) 2*3*5+2*5*10+2*10*2=170
//2 3 4 1 (3,5)(5,10)(10,2)(2,3) 3*5*10+3*10*2+3*2*3=228
//3 4 1 2 (5,10)(10,2)(2,3)(3,5) 5*10*2+5*2*3+5*3*5=160
//4 1 2 3 (10,2)(2,3)(3,5)(5,10) 10*2*3+10*3*5+10*5*10=710
//逆时针
//1 4 3 2 (2,3)(10,2)(5,10)(3,5)头尾接不上
//4 3 2 1
//3 2 1 4
//2 1 4 3
//显然,逆时针不属于该题,讨论的范围。
//该题只需考虑顺时针的情况,松了口气。
//样例通过,提交10分,测试点1,3-10WA,不敢相信
//算法,没问题,怎么可能,重新读题
//发现(4⊕1)=10×2×3=60,理解有误,
//dp[i][i+k]=max(dp[i][i+k],dp[i][j]+dp[j+1][i+k]+a[i]*a[j+1]*a[i+k+1]);//此处写成dp[i][i+k]=max(dp[i][i+k],dp[i][j]+dp[j+1][i+k]+a[i]*a[j+1]*a[i+k]);
//修改,提交0分,全WA,怎么可能
//重读代码,发现,测试语句未删除
//删除测试语句,提交AC。2019-1-27 11:52
//真是一步错,步步错,焦头烂额。
//读好题目,理解好样例是关键。
//突然有一个疑问,NOIP的复赛题,除了简单输入输出数据外,还配了一个复杂的输入输出数据吗?2019-1-27 11:57
#include
#include
int a[210],dp[210][210];
int max(int a,int b){
return a>b?a:b;
}
int main(){
int n,i,j,k,ans=-1;
memset(dp,0,sizeof(dp));
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&a[i]),a[n+i]=a[i];
for(k=1;k
for(j=i;j
dp[i][i+k]=max(dp[i][i+k],dp[i][j]+dp[j+1][i+k]+a[i]*a[j+1]*a[i+k+1]);//此处写成dp[i][i+k]=max(dp[i][i+k],dp[i][j]+dp[j+1][i+k]+a[i]*a[j+1]*a[i+k]);
for(i=1;i<=n;i++)ans=max(ans,dp[i][i+n-1]);
printf("%d\n",ans);
return 0;
}
5.找雷
//P2196 挖地雷
//NOIP 1996 提高组 第3题 共4题
//2019-1-28 20:30翻看了之前编写的代码https://blog.csdn.net/mrcrack/article/details/78440134
//2019-1-29 06:00发现就是最长上升子序列的变形
//感叹,当时能想出,现在怎么没想到呢。
//有进有退,进多退少,总体是进步的。2019-1-29 08:02
//开始编码,有向图,用来判定两点是否联通
//d[i]以i点为结尾的,挖的最多雷
//打印路径过程,稍微有些小障碍,很快修改成功,
//样例通过,提交AC。2019-1-29 08:17
#include
#include
int n,a[25],map[25][25],d[25],pre[25],last;//pre[i]=j i的上一个点来自j
void print_path(int k){
if(k==0)return;
print_path(pre[k]);
if(pre[k]==0)printf("%d",k);
else printf(" %d",k);
}
int main(){
int i,j,ans=0;
memset(map,0,sizeof(map)),memset(pre,0,sizeof(0));
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
for(i=1;i<=n;i++)
for(j=i+1;j<=n;j++)
scanf("%d",&map[i][j]);
for(i=1;i<=n;i++){
d[i]=a[i];
for(j=1;j<=n;j++)
if(map[j][i]&&d[j]+a[i]>d[i])
d[i]=d[j]+a[i],pre[i]=j;
}
for(i=1;i<=n;i++)
if(ans
print_path(last);
printf("\n%d\n",ans);
return 0;
}
//P2196 挖地雷
//NOIP 1996 提高组 第3题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P2196
//N<=20,第1直觉,深搜dfs可行
//选择一条路径,又想到图
//题目写得很清楚,很好懂
//该题需打印路径,需费些心
//看了样例,发现是有向图
//准备采用类Floyd算法,有些累了,先休息。2019-1-27 21:18
//考虑之后,决定用 深搜dfs试试,看看能不能解决路径问题
//在打印路径编写过程中,发现,对递归理解更深刻了。
//出现最大值时,马上存储路径,虽然之后的路径会变。
//样例通过,提交AC。深搜dfs水平确实高了许多。2019-1-28 13:55
#include
#include
int a[25],map[25][25],n,vis[25],ans=0,b[25],path[25];
void dfs(int step,int start,int sum){
int i,j;
if(ans
path[0]=step;
for(j=1;j<=step;j++)path[j]=b[j];
}
for(i=1;i<=n;i++)
if(vis[i]==0&&map[start][i]==1){
vis[i]=1;
b[step+1]=i;
dfs(step+1,i,sum+a[i]);
vis[i]=0;
}
}
int main(){
int i,j;
memset(map,0,sizeof(map));
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
for(i=1;i<=n;i++)
for(j=i+1;j<=n;j++)
scanf("%d",&map[i][j]);
for(i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
vis[i]=1;
b[1]=i;
dfs(1,i,a[i]);//此处写成 dfs(1,i,0);
vis[i]=0;
}
printf("%d",path[1]);
for(i=2;i<=path[0];i++)printf(" %d",path[i]);
printf("\n%d\n",ans);
return 0;
}
并查集
6.亲戚
//1073 家族
//在线测评地址http://codevs.cn/problem/1073/
//该题就是一个裸的并查集
//样例很快通过,提交AC. 2019-1-18
#include
#define maxn 5100
int n,m,p,f[maxn];
int getf(int u){
if(f[u]==u)return u;
return f[u]=getf(f[u]);
}
void merge(int u,int v){
int f1=getf(u),f2=getf(v);
if(f1!=f2)//左靠
f[f2]=f1;
}
int main(){
int i,x,y,f1,f2;
scanf("%d%d%d",&n,&m,&p);
for(i=1;i<=n;i++)f[i]=i;
while(m--){
scanf("%d%d",&x,&y);
merge(x,y);
}
while(p--){
scanf("%d%d",&x,&y);
f1=getf(x),f2=getf(y);
if(f1==f2)printf("Yes\n");
else printf("No\n");
}
return 0;
}
贪心
7.观光公交
heap
8.合并果子
//P1090 合并果子
//NOIP 2004 提高组 第2题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P1090
//用该题演练STL中的堆函数
//样例通过,提交AC。2019-1-28 20:42
//做个说明,弹出元素,从顶部,a[1];加入元素,从尾部,a[n]
//默认是 大根堆。
//若要小根堆,需加cmp函数, a>b
//若加了cmp函数,则make,pop,push函数,均需加此cmp函数。否则,均无法实现功能。
//STL的堆函数处理堆问题,代码量太小了。2019-1-28 20:45
#include
#include
using namespace std;
int n,h[10100];
int cmp(int a,int b){
return a>b;
}
int main(){
int i,ans=0,m,a,b;
scanf("%d",&n),m=n-1;
for(i=1;i<=n;i++)scanf("%d",&h[i]);
make_heap(h+1,h+1+n,cmp);
for(i=1;i<=m;i++){
a=h[1],pop_heap(h+1,h+1+n,cmp),n--;//此处写成 pop_heap(h+1,h+1+n)
b=h[1],pop_heap(h+1,h+1+n,cmp);
ans+=a+b;
h[n]=a+b,push_heap(h+1,h+1+n,cmp);//此处写成 push_heap(h+1,h+1+n)
}
printf("%d\n",ans);
return 0;
}
模拟
9.寻宝
//P1076 寻宝
//NOIP 2012 普及组 第2题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P1076
//题目很长,耐心多读几遍,很重要。
//弄懂题意最好的办法,就是对样例进行模拟,模拟如下:
2(1,2) 1(1,5) 0(0,1) 第2层 第1次出现在 2(1,2) 密码为(3+2)%20123=5 第N层无需再找有楼梯的房间
2(1,4) 1(0,3) 0(1,2) 第1层 第1次出现在 1(0,3) 能上楼的房间 找第3个有楼梯的房间 找到2(1,4)
//比如当前房间的指示牌上写着2,则按逆时针方向开始尝试,找到第2个有楼梯的房间
//上面这句很关键,请注意,不是连续找2个房间,是找2个有楼梯的房间。
//该题需开一个结构体的二维数组,存储房间信息
//该题还需开一个二维数组,逆时针指向有楼梯的房间的序号。
//看了数据范围,二维数组不会爆内存
//采用模运算,不会超时
//样例通过,提交0分,全WA。2019-1-23 20:40
//利用https://www.luogu.org/discuss/show/23296中的数据,进行跟踪
5 4
1 5
1 8
0 5
1 6
0 7
1 65
1 4
0 56
1 8
1 7
1 9
0 11
1 15
1 78
1 98
1 87
1 54
0 45
1 56
1 44
2
153
//b[i][]数组存储无误
//怎么查都查不出,又读了一遍题目,才发现“如果当前房间本身就有楼梯通向上层,该房间作为第一个有楼梯的房间。”
//题意理解有误啊,误以为,上到的这个房间有楼梯,就可以直接到达上一层,其实不是,还需要再找多个房间。
//else{//看题,没抓住题意,导致该else功能的缺失。
//修改,提交0分,全WA。2019-1-23 21:35
//将 近1年前AC的代码,调出来,对比了测试数据的输出情况,才发现
//now变量指的是在b[i][]中的位置,而不是在q[i][]中的位置。
//修改,提交AC。2019-1-23 22:02
//该题是道 纯模拟的题,难在 所有房间, 有楼梯的房间 之间的转换,如本人编写的now变量的意义。
//难得,近1年前一次编写成功,而今,却反复编写,却WA。
//上述数据,执行过程如下:
i=1 start=0 ans=5
i=2 start=1 ans=12
i=3 start=1 ans=19
i=4 start=2 ans=97
i=5 start=3 ans=153
153
//以下为AC代码。
#include
#define mod 20123
struct node{
int have,num;
}q[10010][105];
int b[10010][105],N,M,ans=0,start;
int main(){
int i,j,now;
scanf("%d%d",&N,&M);
for(i=1;i<=N;i++){
b[i][103]=0;//用来存储,有楼梯的房间数
for(j=0;j
if(q[i][j].have)b[i][b[i][103]++]=j;
}
}
scanf("%d",&start);
for(i=1;i<=N;i++){
ans=(ans+q[i][start].num)%mod;
if(!q[i][start].have){
//找到无楼梯房间之前的第1个有楼梯房间
if(start
else{//无楼梯房间在所有有楼梯房间的中间
for(j=0;j
break;
}
}
now=(now+q[i][start].num)%b[i][103];//得到房间序号,在b[i][]中的位置
start=b[i][now];
}else{//看题,没抓住题意,导致该else功能的缺失。
for(j=0;j
now=j;
break;
}
now=(now+q[i][start].num-1)%b[i][103];
start=b[i][now];
}
}
printf("%d\n",ans);
return 0;
}
hash
10.方程的解数
//1735 方程的解数
//NOI 2001 共6题
//在线测评地址http://codevs.cn/problem/1735/
//哈希表为什么要模以素数而非合数,此文讲得非常棒https://blog.csdn.net/zhishengqianjun/article/details/79087525
//哈希表解决此题的思路,该文讲得很好https://blog.csdn.net/fisher_jiang/article/details/667059
//哈希表早就习得,应用是第一次,甚是高兴,理论变现实。
//因计算过程中的数据达到2^31,故采用桶排序,要爆内存,只能采用不爆内存的数组存储
//其中就会遇到冲突,哈希表的算法就十分有用了,
//关键有2个函数,一个是定位在数组中的位置,一个是将元素插入数组
//一个比较大的质数4000037,先编程简单的验证,是否质数
//有个问题,要说明,哈希表中,绝对值相等的正负数,存储位置不一样
//突然发现,英语很重要,是不是要把《新概念英语》背起来呢。
//样例通过,提交AC。2019-2-2 12:07
//该题收获,掌握了哈希表的写法。
#include
#include
#define mod 4000037
#define LL long long
int n,m,k[10],p[10],mid;
int amount[mod],used[mod],ans[mod];
LL cnt=0;
int locate(int x){//只找不改。
int pos;
pos=(mod+x%mod)%mod;//此处写成pos=(x+x%mod)%mod;,拔低了水平//x为负数,x为正数,均可处理,时间复杂度为O(1),处理出来的结果为非负数
while(used[pos]&&ans[pos]!=x){//冲突处理,该处已被占用,且不等于x
pos=(pos+1)%mod;
}//跳出循环,要么该处没被占用;要么该处已被占用,存储的是数x
return pos;
}
void insert(int x){
int pos;
pos=locate(x);
if(used[pos]&&ans[pos]==x)amount[pos]++;//该处已被占用,存储的是数x
else used[pos]=1,ans[pos]=x,amount[pos]++;//该处没被占用; 代码虽然冗余,但是易懂,就不精简了
}
LL quick_pow(int a,int b){
LL ans=1;
while(b){
if(b&1)ans*=a;
a*=a;
b>>=1;
}
return ans;
}
void dfs_left(int step,int sum){//1->mid
int i;
if(step==mid+1){
insert(sum);
return ;
}
for(i=1;i<=m;i++)
dfs_left(step+1,sum+k[step]*quick_pow(i,p[step]));
}
void dfs_right(int step,int sum){//mid+1->n
int i,pos;
if(step+mid==n+1){//此处写成 if(step==n+1)
pos=locate(-sum);// 右边结果等于左边结果的相反数
if(used[pos]&&ans[pos]==-sum)cnt+=amount[pos];
return ;
}
for(i=1;i<=m;i++)
dfs_right(step+1,sum+k[step+mid]*quick_pow(i,p[step+mid]));
}
int main(){
int i;
memset(ans,0,sizeof(ans)),memset(amount,0,sizeof(amount)),memset(used,0,sizeof(used));
scanf("%d%d",&n,&m);
mid=n/2;
for(i=1;i<=n;i++)scanf("%d%d",&k[i],&p[i]);
dfs_left(1,0);
dfs_right(1,0);
printf("%lld\n",cnt);
return 0;
}
//验证4000037是质数的代码如下
#include
#define mod 4000037
int main(){
int i;
for(i=2;i*i<=mod;i++)
if(mod%i==0)printf("No\n");
printf("Yes\n");
return 0;
}
//1735 方程的解数
//NOI 2001 共6题
//在线测评地址http://codevs.cn/problem/1735/
//第一直觉 深搜dfs+剪枝,那点分数应该可以
//指数的p次方,没说明范围,为了减少耗时,决定采用快速幂
//为了尽可能的避免int溢出,决定采用long long
//用两个结构体,一个存非负系数,另一个存负系数
//还好在int范围内测试了2^31=-2147483648,2^31-1=2147483647
//核心,计算非负的绝对值,计算负的绝对值,比较是否相等,相等即为一种解。
//样例通过,提交30分,测试点1,5-10TLE,目前尽力了。2019-2-1 16:13
//以下为30分代码。
#include
#include
#define LL long long
int n,m,cnt_b=0,cnt_c=0;
LL cnt=0;
struct node{
LL k,p;
}b[10],c[10];
LL quick_pow(LL a,LL n){//快速幂
LL ans=1;
while(n){
if(n&1)ans*=a;//此处写成 if(n&2)ans*=a;
a*=a;
n/=2;
}
return ans;
}
void dfs_c(int step,LL sum1,LL sum2){
int i;
if(sum2>=((1<<31)-1))return;
if(sum2>sum1)return;
if(step==cnt_c+1&&sum1==sum2){
cnt++;
return ;
}
if(step==cnt_c+1)return;//漏了此功能,跟踪程序后才发现。此句很重要,足足耽搁了30分钟
for(i=1;i<=m;i++)
dfs_c(step+1,sum1,sum2+c[step].k*quick_pow(i,c[step].p));
}
void dfs_b(int step,LL sum){
int i;
if(sum>=((1<<31)-1))return;
if(step==cnt_b+1){
dfs_c(1,sum,0);
return;
}
for(i=1;i<=m;i++)
dfs_b(step+1,sum+b[step].k*quick_pow(i,b[step].p));
}
int main(){
int i;
LL k,p;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++){
scanf("%lld%lld",&k,&p);
if(k>=0)cnt_b++,b[cnt_b].k=k,b[cnt_b].p=p;
else cnt_c++,c[cnt_c].k=-k,c[cnt_c].p=p;//此处写成else cnt_c++,b[cnt_c].k=k,b[cnt_c].p=p;跟踪了程序才查出
}
dfs_b(1,0);
printf("%lld\n",cnt);
return 0;
}
数论
11.数列
//P1062 数列
//NOIP 2006 普及组 第4题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P1062
//第1直觉,堆+深搜dfs,但是感觉不顺手,寻求它法
//转换成进制,只需系数<=1即可,否则不符合要求,一个想法掠过
//办法是好办法,就是担心超时,不过,很好编写,50分绝对有信心
//程序很快编好,样例通过,开始测试极端情况
//3 1000 29430 很快
//4 1000 349248 很快
//5 1000没有输出,果断将最大值开到10^7 结果为2440750 很快
//6 1000没有输出,果断将最大值开到10^8 结果为12091896 很快
//7 1000 结果为47076750 有些卡顿,但1s能过
//8 1000没有输出,果断将最大值开到10^9 没有输出 有些卡顿,到头了,
//程序需要修改,int需改成long long
//8 1000 将最大值开到10^10 结果为 153387520 明显卡顿,1s过不了
//该算法的极限到了,提交40分,测试点5-10TLE。2019-1-30 18:59
//以下为40分代码。
//突然想到,该题在考察二进制
//第1个数 1
//第2个数 10
//第3个数 11
//第4个数 100
//第5个数 101
//第6个数 110
//第7个数 111
//该题迎刃而解,N转换成2进制的
//N=1000,对应2进制 1111101000
//迅速将stack[100],改成stack[20]
//编好后,马上测试8 1000又快又准,
//测试15 1000,秒出41189262750
//提交AC。2019-1-30 20:55
//完全独立想出,没有任何提示
//看来,看了两集《单挑荒野》还是有收获的,看好后,突然就想到了上述解法。
#include
#define LL long long
int k,N,stack[20],top=0;
LL ans=0;
void to2(int x){//N转2进制
while(x){
stack[++top]=x%2;
x/=2;
}
}
int main(){
int i;
scanf("%d%d",&k,&N);
to2(N);
for(i=top;i>=1;i--){//k进制转10进制
ans*=k;
ans+=stack[i];
}
printf("%lld\n",ans);
return 0;
}
//P1062 数列
//NOIP 2006 普及组 第4题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P1062
//第1直觉,堆+深搜dfs,但是感觉不顺手,寻求它法
//转换成进制,只需系数<=1即可,否则不符合要求,一个想法掠过
//办法是好办法,就是担心超时,不过,很好编写,50分绝对有信心
//程序很快编好,样例通过,开始测试极端情况
//3 1000 29430 很快
//4 1000 349248 很快
//5 1000没有输出,果断将最大值开到10^7 结果为2440750 很快
//6 1000没有输出,果断将最大值开到10^8 结果为12091896 很快
//7 1000 结果为47076750 有些卡顿,但1s能过
//8 1000没有输出,果断将最大值开到10^9 没有输出 有些卡顿,到头了,
//程序需要修改,int需改成long long
//8 1000 将最大值开到10^10 结果为 153387520 明显卡顿,1s过不了
//该算法的极限到了,提交40分,测试点5-10TLE。2019-1-30 18:59
//以下为40分代码。
#include
#define LL long long
int k,N,cnt=0;
int judge(LL x){//0不符,1符合要求
while(x){
if(x%k>1)return 0;//系数 大于 1
x/=k;
}
return 1;
}
int main(){
LL i;
scanf("%d%d",&k,&N);
for(i=1;i<=10000000000LL;i++){// 10000000000LL此句写得不错
if(judge(i))cnt++;
if(cnt==N){
printf("%lld\n",i);
break;
}
}
return 0;
}
12.同余方程
//P1082 同余方程
//NOIP 2012 提高组 day2 第1题 day2 共3题
//在线测评地址https://www.luogu.org/problemnew/show/P1082
//ax+by=1,gcd(a,b)=1,肯定成立,因,输入数据保证一定有解
//扩展欧几里得算法exgcd
//因数据a,b最大值2000000000,采用long long比较稳妥
//解决该题的过程,就是 扩展欧几里得算法 重新推导的过程
//独立推导完成,没有借助任何资料。
//样例通过,提交AC。2019-1-30 16:53
#include
int exgcd(int a,int b,int *x,int *y){
int d,t;
if(b==0){
*x=1,*y=0;
return a;
}
d=exgcd(b,a%b,x,y);
t=*x,*x=*y,*y=t-a/b**y;
return d;
}
int main(){
int a,b,x,y;
scanf("%d%d",&a,&b);
exgcd(a,b,&x,&y);
x=(b+x%b)%b;
printf("%d\n",x);
return 0;
}
13.多项式系数
//P1313 计算系数
//NOIP 2011 提高组 第2天 第1题 第2天 共3题
//在线测评地址https://www.luogu.org/problemnew/show/P1313
//翻看本人之前代码,竟有逆元之说,决定停下脚步,把这些遗忘的知识拾起。
//通过此文https://www.cnblogs.com/rir1715/p/7748054.html瞬间搞懂了,逆元的计算公式。
//逆元有一个要素,模运算的数字需是质数。其中用到了费马小定理
//第1步,先验证10007是质数
//发现是质数,可以开始乘法逆元
//有乘法逆元的地方,就有快速幂
//样例通过,提交AC。2019-1-30 9:57
//乘法逆元有些感觉了。
#include
#define mod 10007
#define LL long long
LL quick_pow(int x,int n){
LL ans=1;
while(n){
if(n&1)ans=(ans*x)%mod;
x=(x*x)%mod;
n/=2;
}
return ans;
}
int main(){
int i,a,b,k,n,m;
LL c=1,A=1,B=1,d=1,ans;
scanf("%d%d%d%d%d",&a,&b,&k,&n,&m);
for(i=k;i>=k-n+1;i--)c=(c*i)%mod;
for(i=n;i>=1;i--)d=(d*i)%mod;
c=(c*quick_pow(d,mod-2))%mod;//乘法逆元
for(i=1;i<=n;i++)A=(A*a)%mod;
for(i=1;i<=m;i++)B=(B*b)%mod;
ans=(c*A*B)%mod;
printf("%lld\n",ans);
}
//P1313 计算系数
//NOIP 2011 提高组 第2天 第1题 第2天 共3题
//在线测评地址https://www.luogu.org/problemnew/show/P1313
//通项公式C(k,n)(ax)^n(by)^(k-n)
//杨辉三角即可解决 C(k,n)
//因对10007取模,int不会溢出
//测算了10007*1000000=10^10,int溢出,还需long long
//for(i=0;i<=k;i++)c[i][i]=c[i][0]=1;//此处写成 for(i=0;i<=k;k++)c[i][i]=c[i][0]=1;查了20分钟
//测试的时候,就觉得奇怪,怎么会超1s,原来是笔误引出的。
//样例通过,提交50分,测试点2,3,6-8 WA.2019-1-30 8:38
//怎么可能,重新读题,对特殊情况,进行理解,没问题啊
//再读代码,又发现一处笔误
//for(i=1;i<=m;i++)B=(B*b)%mod;//此处写成 for(i=1;i<=m;i++)B=(B*a)%mod; 导致提交50分
//修改,提交AC,2019-1-30 8:44
//提交前,还是要多测试,笔误之类的,完全能在测试中发现,这样,提交,更有信心。
#include
#define LL long long
#define mod 10007
int a,b,k,n,m,c[1010][1010];
LL A=1,B=1,ans;
int main(){
int i,j;
scanf("%d%d%d%d%d",&a,&b,&k,&n,&m);
for(i=0;i<=k;i++)c[i][i]=c[i][0]=1;//此处写成 for(i=0;i<=k;k++)c[i][i]=c[i][0]=1;查了20分钟
for(i=2;i<=k;i++)//此处写成 for(i=1;i<=k;i++)
for(j=1;j
for(i=1;i<=n;i++)A=(A*a)%mod;
for(i=1;i<=m;i++)B=(B*b)%mod;//此处写成 for(i=1;i<=m;i++)B=(B*a)%mod; 导致提交50分
ans=(c[k][n]*A*B)%mod;
printf("%lld\n",ans);
return 0;
}
dfs
14.选数
//P1036 选数
//NOIP 2002 普及组 第2题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P1036
//深搜dfs即可解决。
//最大和,5000000*20=10^8,int不会溢出
//样例通过,提交AC。2019-1-22 19:47
//翻看代码,比2年前,写得棒多了。
#include
#define maxn 25
int a[maxn],n,k,cnt=0;
int isPrime(int x){//素数返回1,非素数返回0
int i;
if(x==1)return 0;
if(x==2)return 1;
for(i=2;i*i<=x;i++)
if(x%i==0)return 0;
return 1;
}
void dfs(int step,int start,int sum){
int i;
if(step==k+1){
if(isPrime(sum))cnt++;
return ;
}
for(i=start;i<=n;i++)
dfs(step+1,i+1,sum+a[i]);//此处写成i+1甚为精妙
}
int main(){
int i;
scanf("%d%d",&n,&k);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
dfs(1,1,0);
printf("%d\n",cnt);
return 0;
}
高精度
15.回文数
//P1015 回文数
//NOIP 1999 提高组 第2题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P1015
//测算int或是long long 是否会溢出
//98+89=187 187+781=968 968+869=1837 1837+7381=9218
//9218+8129=17347 17347+74371=91718 91718+81719=173437
//173437+734371=907808 907808+808709=1716517
//1716517+7156171=872688
//受不了了,还是编个程序测试了再说
//测试98,int没有溢出,测试99,int溢出
//想过用long long,但该题已经没有意义,因为是设计N进制
//改成字符串,省时省力,用高精度加
//该题,还需特判,如,输入的数,本身就是回文
//读题,发现进制数M(100位之内),看成了100之内,还好及时发现
//因涉及16进制,故不采用int
//再想想,加法计算不好处理,决定还是从char a[]回归到int a[]
//样例通过,提交25分,测试点1,2,4 WA
//这么简单的题,怎么会错,仔细想了想,做该题过程中,被打断了四次
//错也难怪,错了之后,马上想到,是M进制,编的过程中,写成了10进制
//马上修改,提交75分,测试点2 WA。
//翻看了https://www.luogu.org/discuss/show/53147讨论,输入数据也可以是16进制,昏倒
//缺失没考虑到
//修改,提交AC。2019-1-24
#include
#include
#define maxn 1000000
int N;
int a[maxn],b[maxn],c[maxn];
char s[maxn];
int judge(int *s){
int i;
for(i=1;i<=s[0]/2;i++)
if(s[i]!=s[s[0]-i+1])
return 0;//非回文
return 1;//回文
}
void reverse(int *x,int *y){
int i;
y[0]=x[0];
for(i=1;i<=x[0];i++)y[x[0]-i+1]=x[i];
}
void add(int *x,int *y){
int i;
memset(c,0,sizeof(c));
c[0]=x[0];
for(i=1;i<=c[0];i++){
c[i]+=x[i]+y[i];
c[i+1]+=c[i]/N;//此处写成 c[i+1]+=c[i]/10;
c[i]%=N;//此处写成c[i]%=10;
}
if(c[i])c[0]=i;
memcpy(a,c,sizeof(c));
}
int main(){
int i;
scanf("%d%s",&N,s+1);
a[0]=strlen(s+1);
for(i=1;i<=a[0];i++)
if('A'<=s[i]&&s[i]<='F')a[i]=s[i]-'A'+10;
else if('a'<=s[i]&&s[i]<='f')a[i]=s[i]-'a'+10;
else a[i]=s[i]-'0';//只考虑了0-9
if(judge(a))printf("STEP=0\n");//特判
else{
for(i=1;i<=30;i++){
reverse(a,b);
add(a,b);
if(judge(a)){
printf("STEP=%d\n",i);
break;
}
}
if(i==30+1)printf("Impossible!\n");
}
return 0;
}
模拟
16.现在几点钟
//1063: 现在几点钟?
//在线测评地址http://218.5.5.242:9018/JudgeOnline/problem.php?id=1063
//问题中,表述的东西比较多
//按先特判,再一般情形,程序会比较容易编写。
//测试了几组时间数据的读取
//1:00 读入1 0
//1:03 读入1 3
//开始进行特判的处理
//突然发现,英语没学好的,这个题目难以做好,有一堆单词要独立写出
//编写一个时间,测试一个时间
//问题中给的数据全部通过,提交AC。眼泪都要掉下来了,生怕英文单词写错
//基本可判定,问题中给出的数据,就是该问题的测试点。2019-1-22 21:05
//该题,主要在练,if else + 字符串简单处理。
#include
#include
int h,m;
char num[][20]={"","one","two","three","four","five","six","seven","eight","nine","ten","eleven","twelve","thirteen","fourteen","fifteen","sixteen","seventeen","eighteen","nineteen","twenty","thirty","forty"};
char ten[][20]={"","","twenty","thirty","forty"};
int main(){
char s[20];
scanf("%d:%d",&h,&m);
if(m==0){//5:00 Five o'clock
strcpy(s,num[h]);
s[0]=s[0]-'a'+'A';
printf("%s o'clock\n",s);
}else if(m==15){//5:15 Quarter past five
printf("Quarter past %s\n",num[h]);
}else if(m==45){//5:45 Quarter to six
if(h==12)h=1;//要小心12 与 1的关系
else h+=1;
printf("Quarter to %s\n",num[h]);
}else if(m<45){
strcpy(s,num[h]);
s[0]=s[0]-'a'+'A';
printf("%s ",s);
if(m<=20)printf("%s",num[m]);//10:10 Ten ten
else{//9:22 Nine twenty-two 2:30 Two thirty 6:40 Six forty
printf("%s",ten[m/10]);
if(m%10)printf("-%s",num[m%10]);
}
}else if(m>45){//8:47 Thirteen to nine 12:47 Thirteen to one (American time: 1:00 follows 12:00)
strcpy(s,num[60-m]);
s[0]=s[0]-'a'+'A';
printf("%s",s);
if(h==12)h=1;//要小心12 与 1的关系
else h+=1;
printf(" to %s",num[h]);
}
return 0;
}
17.选择客栈
//P1311 选择客栈
//NOIP 2011 提高组 day1 第2题 day1 共3题
//在线测评地址https://www.luogu.org/problemnew/show/P1311
//有O(n)的算法,那么要好好学习
//https://www.luogu.org/problemnew/solution/P1311的作者: ShawnZhou可以看看
//以下是改进,更易于理解。
//思路,有些类似 归并排序求逆序对,最长上升子序列。都是以i为结尾的情况分析。
//样例通过,提交AC。2019-1-31 22:54
#include
#include
#define LL long long
#define maxn 55
int cnt[maxn],last[maxn],sum[maxn];//cnt[j]j颜色的数量 last[j] j颜色历此次最近一次出现的位置 sum[j] j颜色在now位置之前(包含)出现的次数
int main(){
int i,now=0,color,price,n,k,p;
LL ans=0;
scanf("%d%d%d",&n,&k,&p);
memset(cnt,0,sizeof(cnt)),memset(last,0,sizeof(last));
for(i=1;i<=n;i++){
scanf("%d%d",&color,&price);
if(price<=p)now=i;//更新最新喝咖啡客栈位置
if(now>=last[color])sum[color]=cnt[color];//在now之前(包含)color客栈的数量
ans+=sum[color];//以客栈i为结尾的符合条件的客栈的个数,有点象 归并排序求逆序对
last[color]=i;//更新color客栈最新位置
cnt[color]++;
}
printf("%lld\n",ans);
return 0;
}
//P1311 选择客栈
//NOIP 2011 提高组 day1 第2题 day1 共3题
//在线测评地址https://www.luogu.org/problemnew/show/P1311
//因n=200000,算法的时间复杂度,要么O(n),要么O(nlogn).
//该题,要得50分,即n=1000,采用O(n^2)的算法,还是比较简单的
//sum[i][j]以i客栈为结尾j颜色客栈的数量
//该题纯模拟+数组的组合知识 即可。
//int可能溢出,考虑用long long
//样例通过,提交AC。2019-1-31 18:23
//纯模拟,算法的时间复杂度O(nk)
//自我感觉,这个算法程序易编出,也不容易出错。
#include
#include
#define LL long long
int n,k,p,q[200010],color[55],b[200010];//b[i] i位置的颜色
LL sum[200010][55],ans=0;
int main(){
int i,j,c,consume,now;
memset(sum,0,sizeof(sum)),memset(color,0,sizeof(color));
scanf("%d%d%d",&n,&k,&p);
for(i=1;i<=n;i++){//时间复杂度nk,应该能险过
scanf("%d%d",&c,&consume);//此处写成 scanf("%d%d",&c,consume); 查了会
color[c]++,b[i]=c;
for(j=0;j
}
now=0;
for(i=1;i<=n;i++)
if(q[i]<=p){
for(j=0;j
ans+=(sum[i-1][j]-sum[now][j])*(sum[n][j]-sum[i-1][j])+sum[n][j]-sum[i][j];
else//最低消费客栈,不参与住宿 1 2 3(最低消费,不参与住宿) 4 5 2*2=4
ans+=(sum[i-1][j]-sum[now][j])*(sum[n][j]-sum[i-1][j]);
now=i;
}
printf("%lld\n",ans);
return 0;
}
18.机器翻译
//P1540 机器翻译
//NOIP 2010 提高组 第1题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P1540
//队列
//样例通过,提交AC。2019-1-23 17:25
//感觉,比起从前,该题变得太轻松了。
#include
#include
#define maxn 1100
int q[maxn],h,t;
int main(){
int m,n,a,i,cnt=0;
memset(q,0,sizeof(q));
scanf("%d%d",&m,&n);
h=t=1;
while(n--){
scanf("%d",&a);
for(i=h;i
if(i==t){//i==t发生在,没找到该单词
cnt++;
if(t-h
else//清理内存,加入内存
h++,q[t]=a,t++;
}
}
printf("%d\n",cnt);
return 0;
}
19.计算器的改良
//P1022 计算器的改良
//NOIP 2000 普及组 第1题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P1022
//该题有现实意义,有些计算器提供了解方程的功能
//读完题,没什么好思路,纯模拟
//字符串读入,之后进行解析,处理
//测试了,3+-3发现能正确运算,3--3报错,-3+-3能正确运算,-3--3报错
//考什么呢,不过需求来源于生活,首要就是将其解决,再考虑优化
//对样例进行研究
//6a-5+1=2-2a a=0.750
//6a-5+1=-2a+2 a=0.750
//提交AC。2019-1-31 12:18
//从左往右扫的过程中,找出数字是关键,数字之前是符号,数字之后是未知数或等号或符号,等号之前是未知数或数字
//该题纯模拟,没有什么技巧,不过需注意一些特殊情况。
#include
#include
char s[1000];
int main(){
int i,len,op,d,fm=0,fz=0,right=0;//op为1表示负数,op为0表示正数 fm分母,fz分子
char alpha;
scanf("%s",s);
len=strlen(s);
i=0;
while(i
while('0'<=s[i]&&s[i]<='9'){
if(i-1<0)op=0;
else if(s[i-1]=='+')op=0;
else if(s[i-1]=='=')op=0,right=1;
else if(s[i-1]=='-')op=1;
d*=10,d+=s[i]-'0',i++;
}//数字处理
if('a'<=s[i]&&s[i]<='z'){//未知数及系数处理
alpha=s[i];
if(right==0){
if(d==0)fm+=1;
else if(op==0)fm+=d;
else if(op==1)fm-=d;
}else{
if(d==0)fm-=1;
else if(op==0)fm-=d;
else if(op==1)fm+=d;
}
}else if(right==0){
if(op==0)fz-=d;
else if(op==1)fz+=d;
}else if(right==1){
if(op==0)fz+=d;
else if(op==1)fz-=d;
}
if(s[i]=='=')right=1;//漏了此句,通过测试数据6a-5+1=-2a+2 a=0.750,发现了疏漏
i++;
}
printf("%c=%.3lf\n",alpha,fz*1.0/fm);
return 0;
}
20.分数线划定
//P1068 分数线划定
//NOIP 2009 普及组 第2题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P1068
//排序采用sort函数
//样例通过,提交,再次遇到Compile Error,爆0
//可怜的windows下的C++编成,头文件,缺失,编译器竟然不提示
//添加头文件,提交AC。2019-1-23
//感觉编得比以前轻松,但是C++隐患太大,需到linux环境中,C++编写,才有保障
#include
#include
#include
using namespace std;
#define maxn 5100
struct node{
int seq,score;
}q[maxn];
int cmp(const struct node &a,const struct node &b){//自大到小
if(a.score==b.score)return a.seq
int main(){
int n,m,i,p,cnt,score;
memset(q,0,sizeof(q));
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)scanf("%d%d",&q[i].seq,&q[i].score);
sort(q+1,q+1+n,cmp);
cnt=p=(int)(m*1.5);
score=q[cnt].score;
while(q[cnt+1].score==score)cnt++;//从p位置开始数
printf("%d %d\n",score,cnt);
for(i=1;i<=cnt;i++)printf("%d %d\n",q[i].seq,q[i].score);
return 0;
}
进制
21.进制转换
//P1017 进制转换
//NOIP 2000 第1题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P1017
//做惯了 正数 正基数,突然遇到了 负基数 正数或负数
//卡顿了很长时间,
//反复对比 正数 正基数,以及 余数 需小于 负基数的绝对值 ,才基本明白该题中的进制转换
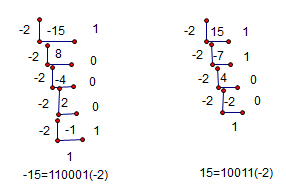
//-15,-2;15,-2模拟如下
//该题难在,思考出上述模拟过程
//需简单测试,负数的除模运算。
//-15/-2=7,-15%-2=-1;15/-2=7,15%-2=1
//负数没法用除模运算,得自己编;正数还能用用
//-15/-2这样处理15/2=7,商7+1=8,余数-15-(-2*8)=1
//因输入是10进制,输入处理就比较轻松。
//N=0需特判
//在犹豫,16进制打印大写字母,还是小写字母,发现样例4已经给出了结果
//样例通过,提交AC.2019-1-29 20:06
//为了弄清,栈空间,做了如下测试。
//-32768 -2
//-32768=1000000000000000(base-2)
//32767 -2
//32767=11000000000000011(base-2)
//空间开100足以
//修改,提交AC。2019-1-29 20:10
#include
int N,R,m,s;//m对应负数N的绝对值,s对应负数R的绝对值
int stack[100],top=0;//开多少位比较合适呢?不要小气,大气些,先开10000,具体可编好后测试,测试发现100足以
int main(){
int i;
scanf("%d%d",&N,&R);
printf("%d=",N);
if(N==0){//N=0需特判
printf("0(base%d)\n",R);
return 0;
}
while(N){
if(N<0){
m=-N,s=-R;
if(m%s==0){//能整除
N=m/s;
stack[++top]=0;
}else{//不能整除
stack[++top]=N-(m/s+1)*R;
N=m/s+1;
}
}else{//N>0
stack[++top]=N%R;
N/=R;
}
}
for(i=top;i>=1;i--){
if(stack[i]<10)printf("%d",stack[i]);
else printf("%c",stack[i]-10+'A');
}
printf("(base%d)\n",R);
return 0;
}
枚举
22.一元三次方程求解
//P1024 一元三次方程求解
//NOIP 2001 提高组 第1题 共4题
//在线测评地址https://www.luogu.org/problemnew/show/P1024
//因根的范围在-100-100之间,精确到小数点后2位 ,只需计算-100.00-100.00
//为了更精确,计算-100.0000-100.000即可,需算2000000,稳过,综上所述,该题傻算即可。
//样例没通过,重新看了题目,发现4个实数A,B,C,D,之前误以为是4个整数,还好样例没通过,马上修改
//发现 return fabs(a*x*x*x+b*x*x+c*x+d);//此处写成 return a*x*x*x+b*x*x+c*x+d;
//应是比较的绝对值
//提交AC。2019-1-24
//对比了该题之前编写的代码,发现应试能力有了大大的提高。
#include
#include
#define eps 1e-7
double f(double a,double b,double c,double d,double x){
return fabs(a*x*x*x+b*x*x+c*x+d);//此处写成 return a*x*x*x+b*x*x+c*x+d;
}
int main(){
int i,cnt=0;
double a,b,c,d,x;
scanf("%lf%lf%lf%lf\n",&a,&b,&c,&d);
for(i=0;i<=2000000;i++){
x=-100+0.0001*i;
if(f(a,b,c,d,x)<=eps){
printf("%.2lf ",x);
cnt++;
if(cnt==3)break;
}
}
return 0;
}