【一】复数与虚数

 一.复数的起源

人们最初认识的数是自然数，然后为了表示没有，引入了0；为了处理小数部分是有限或为无限循环的数引进了有理数的，小数部分是无限不循环的数称为无理数；为了表示赊欠，  又引入了负数。到此为止，实数都已经推出来了。

后来又遇到一个问题，-1的平方根是什么？显然，实数域里面是没有解得。可是，-1的平方根有很有用，例如求解一元二次方程。于是，人们就定义：

                                                                                   ，

并且定义了所有形式为：

                                                                                  

的数，也就是复数，这样高中遇到的一元二次方程总算有解了。

到了这一步，一个很自然的问题就是：那么i的平方根又是什么？仔细算算会发现，i的平方根就等于：​​​或者

，就是两个完全正常的复数。以后，不用再扩大数域，在复数域就能解决所有的开方问题，这真是复数的了不起之处。

​​​​​知乎匿名用户有个回答很有趣：

                                     

复数没有物理意义，一切数学都没有物理意义，比如1+1＝2是没有物理意义的，因为它没有描述任何物理现象。但是，1个苹果＋1个苹果＝2个苹果就有物理意义了，因为它描述了一个物理现象（这其中，苹果才是有物理意义的）。因此，数学没有物理意义，但是物理需要数学来描述物理现象。

结论，复数没有物理意义，复数对物理而言，更应该说是描述物理现象的工具。

二.复数的意义

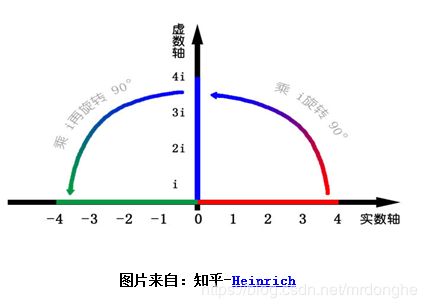
1.旋转

考虑 以及，如果横轴为实数轴，纵轴为虚数轴（实数轴，虚数轴构成复平面，complex plane）的话，将实数轴上的 4，向左旋转了 90°，继续作用于 又让其左旋了 90°， 即是让其左旋 180°。

                                                      

 复数的定义既然 i 表示旋转量，我们就可以用 i ，表示任何实数的旋转状态

只要确定横坐标和纵坐标，比如( 1 , i )，就可以确定某个实数的旋转量（45度）。

数学家用一种特殊的表示方法，表示这个二维坐标：用 + 号把横坐标和纵坐标连接起来。比如，把 ( 1 , i ) 表示成 1 + i。这种表示方法就叫做复数（complex number），其中 1 称为实数部，i 称为虚数部。

 

2.保留维度信息

 复数实部和虚部两部分构成正交单位基，用一个式子表示维度为二的数域，以及复数乘法同时实现幅度运算和角度加减。即复数的本质是引入一个平方为-1的底基i，即由1和i张成的二维空间。复数最神奇的是既可以作为二维坐标参与加法又可以视为坐标变换参与乘法，两种性质的统一是二维代数的特殊性决定的。而这种性质并不是普遍存在的，其他维度都没有，两种角色必须分开。

复数实现让高维参与运算，并且拥有实数那样好的性质。因为高维对象可以带着几何信息参与运算，用实数表示的坐标计算可以丢失几何信息。

打个比方，如果已知，在某一个时刻，有一个正弦信号在一个节点上，它的幅度是1V。那么我是没有办法知道在这一时刻，这个节点上的电压的绝对值是多少的。想要知道这一时刻电压的绝对值，就必须要知道这一时刻这个正弦信号的相位是什么。

另外一个问题是，一个正弦信号在传播的过程中，在通过某个系统以后，它的幅度和相位都有可能发生改变。我得想个办法，同时描述相位和振幅，这样才能更有效地用公式来描述一个信号，或者用公式来描述一个系统对信号的响应。 这个点到平面原点的距离，就恰好能描述一个信号的振幅，而这个点到原点连线以后跟实轴所成的角度呢，恰好能够描述信号的相位。

于是复数的物理意义在于：给物理学家一个机会，去优雅地处理正弦信号。简洁地同时描述幅度和相位的变化。

三.关于复数的几个问题

1.虚数乘法

任何复数 ，都可以改写成旋转半径 r 与横轴夹角 θ 的形式。
假定现有两个复数 和 ，可以将它们改写如下：
a + bi = r1 * ( cosα + isinα )
c + di = r2 * ( cosβ + isinβ )
这两个复数相乘，( a + bi )( c + di ) 就相当于
r1 * r2 * ( cosα + isinα ) * ( cosβ + isinβ )
展开后面的乘式，得到
cosα * cosβ - sinα * sinβ + i( cosα * sinβ + sinα * cosβ)
根据三角函数公式，上面的式子就等于
cos(α+β) + isin(α+β)
所以，
( a + bi )( c + di ) ＝ r1 * r2 * ( cos(α+β) + isin(α+β))
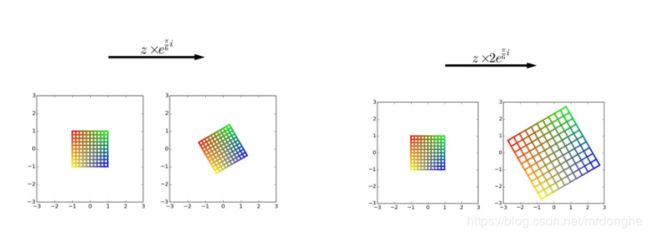
这就证明了，两个复数相乘，就等于旋转半径相乘、旋转角度相加。

例：，各点乘以的后果是平面逆时针旋转弧度：

（，i为复数表示，为极坐标表示）

乘以一个一般的复数，就是把整个平面按它对应的角度旋转弧度，再均匀放大倍。

比如，一条船的航向是 。如果该船的航向，逆时针增加45度，请问新航向是多少？
45度的航向就是 。计算新航向，只要把这两个航向 与 相乘就可以了：。
所以，该船的新航向是 。
如果航向逆时针增加90度，就更简单了。因为90度的航向就是 ，所以新航向等于：。
这就是虚数乘法的物理意义：改变旋转角度。

【可以将复数乘法与实数乘法类比，复数乘法结果不仅包括模的变化，还包括旋转角度的变化。】

2.虚数的加法

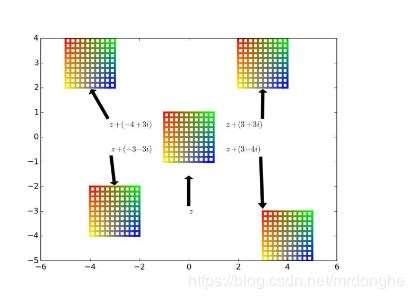
比如，物理学需要计算"力的合成"。假定一个力是 3 + i ，另一个力是 1 + 3i，请问它们的合成力是多少？
根据"平行四边形法则"，你马上得到，合成力就是 ( 3 + i ) + ( 1 + 3i ) = ( 4 + 4i)。
这就是虚数加法的物理意义。

 

如果从图像角度来看的话，加法就是平面的平移，平移量恰好是那个复数对应的平面向量。

3.复数可以用向量表示,且复数的加减法也同于向量的加减法,但复数有乘法,向量有没有与复数对应的乘法呢?

 既有大小又有方向的量叫做向量。

（1）向量积可以被定义为：。

模长：（在这里θ表示两向量之间的夹角(共起点的前提下)（0° ≤ θ ≤ 180°），它位于这两个矢量所定义的平面上。）

（2）向量的大小，也就是向量的长度(或称模)。向量的模记作

（3）数量积

定义：已知两个非零向量a,b，作OA=a,OB=b，则∠AOB称作向量a和向量b的夹角，记作θ并规定0≤θ≤π

定义：两个向量的数量积（内积、点积）是一个数量（没有方向），记作a·b。若a、b不共线，则；若a、b共线，则。
向量的数量积的坐标表示：a·b=x·x'+y·y'。

4.复数的四则运算

​​​对于两个复数： 和  ,

---

注：本文整理网上资料，包括知乎、博客等，如有侵权立刻删除。