强化学习：动态规划算法实现一个简单的示例

一. 问题描述

1.MDP四元组和累积奖赏参数

MDP四元组：
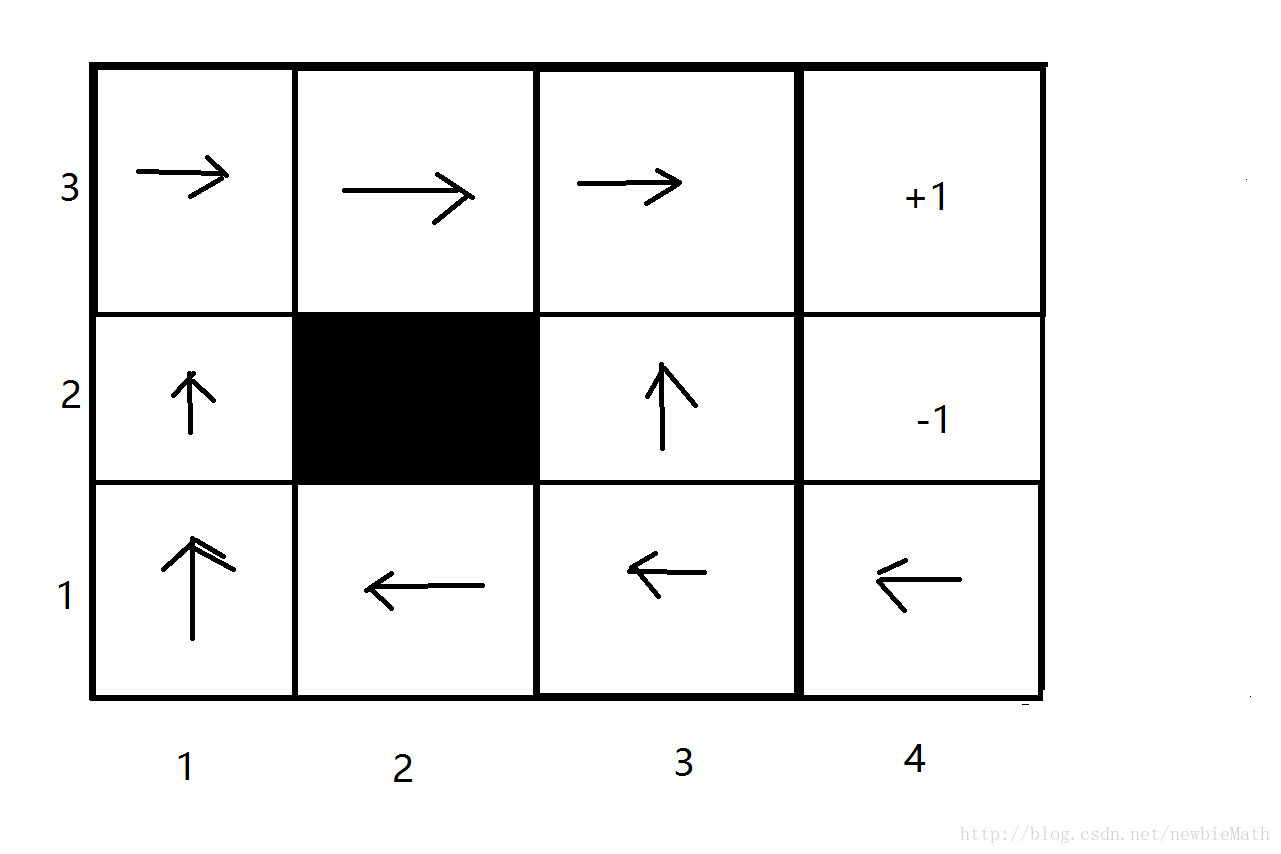
- 状态集合S：图中除去黑色阴影的小格，其他11个格子分别代表一个状态，(2,4)和(3,4)代表终止状态。
- 决策集合A：A=[‘north’, ‘east’, ‘west’, ‘south’]表示四个移动方向。
- 状态转移分布P=( ps,a(s′) ): 在某个状态s ∈ S, 若采取行动方向a，则s以0.8的概率按照a方向移动到 s′ , 以0.1的概率按照a的左侧方向移动，以0.1的概率按照a的右侧方向移动；如果移动方向没有S中的状态，则停留在原地；如果s是终止状态，则始终停留在原地。
- 奖励函数R: 如图，对于每个状态 s∈S , 都对应一个奖励值（图中格子上的数值）；若某次行动移动到该状态，则得到对应的奖励值。
累积奖赏参数：
这里采用T步累积奖赏。

2.问题：

求每个状态s下的最优策略 π∗(s) 。

二. 策略迭代步骤

1.输入和初始化：

• 输入： MDP四元组 E=<S,A,P,R> ; 累积奖赏参数T。
• 初始化： V(s)=0,s∈S ; π(s,a)=1|A|,s∈S,a∈A 。

2.策略估计：

对所有的 s∈S ,

VπT=Eπ[1T∑k=1TRk|s0=s]=Eπ[1TRt+1+T−1T1T−1∑k=2TRt+k|s0=s]=∑aπ(a,s)∑s′Ps′(s,a)[1TRs′(s,a)+T−1TVπT−1(s′)]

Mark: 当 |Vk−Vk+1| 足够小时，终止过程

3.策略优化：

对所有的 s∈S ,

π′(s)=argmaxaQπ(s,a)=argmaxa∑s′ps′(s,a)[1TRs′(s,a)+T−1TVπ(s′)]

Mark: 当 π′=π 时，终止过程

4. 算法伪代码：

输入：MDP四元组E;累积奖赏参数T
过程：
1. 初始化：V(s)=0; π(s,a)=1|A|
2. for t=1,2,… do
3.         V′=∑aπ(s,a)∑s′Ps′(s,a)[1tRs′(s,a)+t−1tV(s′)]
4.         if t==T+1 then
5.                 break
6.         else
7.                 V=V′
8.         end if
9. end for
10. policy_stable=True
11. while policy_stable:
12.         π′(s)=argmaxaPs′(s,a)[1TRs′(s,a)+T−1TV(s′)]
13.         if π′==π then
14.                 break
11.         else
12.                 π=π′
13.         end if
14. end while
输出： 最优策略 π

三. 代码实现

python代码：

import numpy as np
###part1:输入MDP四元组, 累积奖赏参数T
S=[(1,1),(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4)];size_state=len(S);#状态向量
final_state=[(2,4), (3,4)]
A=['n', 'e', 'w', 's'];size_action=len(A);#actions向量
P=[];#转移概率矩阵
for i in range(size_state):
    if S[i] in final_state:
        action_state=[{i:1},{i:1},{i:1},{i:1}]
    else:
        action_state=[]
        for j in range(size_action):
            state=S[i]; action=A[j];
            if action=='n':
                state_pro={i:0}
                next_state=(state[0]+1, state[1])
                if next_state in S:
                    state_pro[S.index(next_state)]=0.8;
                else:
                    state_pro[i]=state_pro[i]+0.8;
                next_state=(state[0], state[1]+1);
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1;
                next_state=(state[0], state[1]-1)    
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1
                action_state.append(state_pro)
            elif action=='e':
                state_pro={i:0}
                next_state=(state[0], state[1]+1)
                if next_state in S:
                    state_pro[S.index(next_state)]=0.8;
                else:
                    state_pro[i]=state_pro[i]+0.8;
                next_state=(state[0]+1, state[1]);
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1;
                next_state=(state[0]-1, state[1])    
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1
                action_state.append(state_pro)
            elif action=='w':
                state_pro={i:0}
                next_state=(state[0], state[1]-1)
                if next_state in S:
                    state_pro[S.index(next_state)]=0.8;
                else:
                    state_pro[i]=state_pro[i]+0.8;
                next_state=(state[0]+1, state[1]);
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1;
                next_state=(state[0]-1, state[1])    
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1
                action_state.append(state_pro)
            else:
                state_pro={i:0}
                next_state=(state[0]-1, state[1])
                if next_state in S:
                    state_pro[S.index(next_state)]=0.8;
                else:
                    state_pro[i]=state_pro[i]+0.8;
                next_state=(state[0], state[1]+1);
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1;
                next_state=(state[0], state[1]-1)    
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1
                action_state.append(state_pro)
    P.append(action_state)
             R=np.array([-0.02,-0.02,-0.02,-0.02,-0.02,-0.02,-1,-0.02,-0.02,-0.02,1]); # rewards
T=40;#累积步长
###part2:初始化
value=np.zeros(size_state); #初始化value
policy=np.zeros((size_state, size_action))+1/size_action;# 初始化policy
###part3:策略估计
T_MAX=1000;
for t in range(1,T_MAX+1):
    value_new=np.zeros(size_state);
    for state in range(size_state):#对所有s,计算对应的value
        for action in range(size_action):#对某个s,按照当前策略选取a
            state_action_state=P[state][action]
            q_state_action=0
            for next_state in state_action_state:#(s, a)下，转移到s'的概率
                trans_pro=state_action_state[next_state]
                q_state_action=q_state_action+trans_pro*(R[next_state]/t+value[next_state]*(t-1)/t);   
            value_new[state]=value_new[state]+policy[state][action]*q_state_action
    if t==T+1:
        break
    else:
        value=value_new[:]
###part3:选取最优策略
new_policy=[0 for i in range(size_state)];
opt_policy=[0 for i in range(size_state)];
policy_stable=True
while policy_stable:
    for state in range(size_state):#对所有s,求对应的最优策略a
        q_state_actions=[]
        for action in range(size_action):#对某个s,对所有可能采取的a计算Q(s, a)
            state_action_state=P[state][action]
            q_state_action=0
            for next_state in state_action_state:
                trans_pro=state_action_state[next_state]
                q_state_action=q_state_action+trans_pro*(R[next_state]/T+value[next_state]*(T-1)/T);
            q_state_actions.append(q_state_action)

        new_policy[state]=q_state_actions.index(max(q_state_actions));
    if new_policy==opt_policy:
        policy_stable=False
    else:
        opt_policy=new_policy

###输出结果
print('opt_policy:', opt_policy)       

输出结果：

opt_policy: [0, 2, 2, 2, 0, 0, 0, 1, 1, 1, 0]

opt_policy中第i个元素的值k表示的是 π(S[i])=A[k] 。
图像展示：

四：参考资料

斯坦福公开课：机器学习