遗传算法的matlab实现

      遗传算法（Genetic Algorithm，GA）是20世纪70年代初兴起的一门新兴学科。遗传算法的基本思想来源于达尔文的进化论和孟德尔的遗传学说，它通过模拟生物进化的过程来求解问题。生物中的基因对应优化问题中的变量组合，一个解则代表了一个个体。通过生物基因的交叉与变异来改变种群的性状（函数值）。通过进化过程中优胜劣汰的原则挑选出优秀的个体（函数值大或小），最终通过迭代的方式模拟生物的进化，得到一个适合生存于特定环境的种群，以此来求解出优化问题的全局最优解。

      遗传算法已经发展得很成熟，广泛应用于优化问题的求解。
①遗传算法只对个体的基因进行操作，所以无论实际问题多么复杂，其稳定性都不会受到太大的影响。
②遗传算法的搜索过程属于并行计算，能够很好地搜索解空间。
③稳定性、鲁棒性强，适用于非线性、高维复杂优化问题。

      其流程如下：

      初始化种群相当于确定原始解的位置，交叉是利用亲代信息来生成下一代个体，变异是基因的变异，并以此来丰富基因匹配的种类，适应度即构造的函数所对应的函数值，自然选择是根据特定的规律选择进入下一代的个体。         其涉及到的算法参数有：

      种群数量：每一次迭代中保留下来的个体数量，一般设置为20~200，少了算法稳定性差，多了增加计算量且求解能力不是线性提升。
      迭代次数：种群的进化代数，简易的问题100代~300代即可，1000代左右最常见，若问题复杂度高，可以适当增加迭代次数。
      交叉概率：个体进行基因交叉的概率，通常取为0.3~0.9。
      变异概率：个体基因突变的概率，通常取为0.001~0.1。对于遗传算法的原型而言，变异概率大了，种群不稳定。

      遗传算法中基因的编码方式大致有二进制编码、十进制编码这两种，二进制编码属于算法原型中的编码方式，因其转码时会徒增额外的计算量，且在做离散型编码时，二进制远没有十进制便捷、快速，故笔者不推荐使用二进制的编码方式，后续的例题将在基于十进制编码的基础上进行讲解，对二进制编码感兴趣的同学可以自己去尝试，对比一下究竟哪种方法更好。
      但不管你使用何种编码方式，都要求任意一个解对应的编码应该是独一无二的，且基因突变时每个基因出现的概率应该满足均匀分布，只要满足了这两个条件，使用什么编码都无所谓，只是计算机上的计算速度不同而已。

      同样地，我们结合例子来理解：

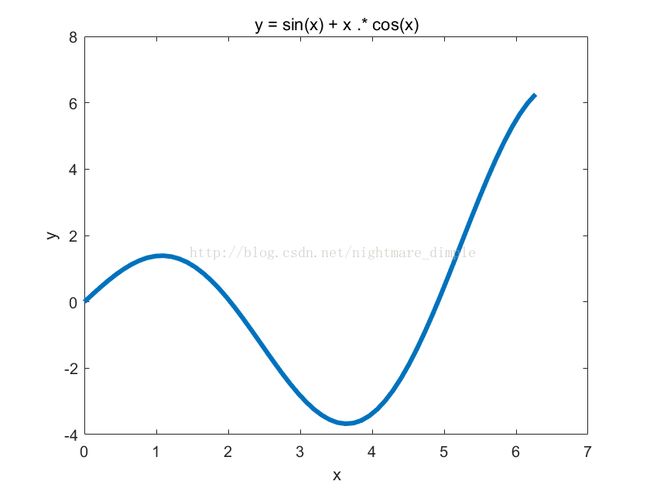
      现有一个函数，y = sin(x) + x * cos(x)，求该函数在区间[0,2π]上的最大值。首先我们需要画出函数的图像，如下图：

     几乎所有的实际问题转化成函数之后都无法画出图像，这里只是为了好观察才画图的，解决问题的第一步就像之前说的，先编码，该问题中只有一个变量需要编码，即x。

• 编码

      假设编码长度取5，即将求解区间划分了10^5份，但是要注意第一份是0，而不是1，长度越长精度越高。

      解码的方式非常简单，举个例子，基因12345对应的x就是12345÷99999×(2π-0)+0 ~= 0.7757 。可以很明显的看出，基因00000代表x = 0，99999代表x = 2π 。对于连续型的问题编码大多采取这样的方式，但对于离散型的编码，需要根据具体的问题而设计，编码设计的优劣直接影响算法最终的结果。
     离散型的编码也很常见，如TSP问题的编码、NP问题的编码等决策型的实际问题大多都需要使用离散型编码，基础阶段不要深究这个，此处不多做介绍。

• 交叉

      交叉是遗传算法中一个非常重要的操作，其优劣影响算法的收敛速度。假设需要交叉的基因为 12345 与 66666，则断点随机取3，将第三个位置之后的序列交换生成两个新解，123 66与666 45 。这个应该很好理解，断点的选取应满足均匀分布。

• 变异

      变异是遗传算法中另一个重要的操作，其优劣影响算法的最终结果与全局最优的接近程度。假设满足变异条件的基因为 66666，则当变异点随机取2时，将第二个位置处的值随机替换，生成一个新解，6 0 666 。这个0的生成与变异点的选取应该满足均匀分布。也就是变异成6 8 666也是可以的，且这两个出现的期望应该相等。

• 自然选择

       通常来说，自然选择包括轮盘法和排名法。

       轮盘法是通过每个个体与总体的适应度占比来衡量其优劣，比值越大越不容易被淘汰，当然轮盘法的计算法复杂度也相对较高：Pi = Fi ÷ ΣF
       排名法是通过每个个体的适应度排名来看的，排名越靠前越不容易被淘汰，排名法的计算法复杂度相对较低：Pi = Ri ÷ N 或 P = (Ri - 1) ÷ N 

      Pi 是第i个个体被淘汰的概率，Fi 是第i个个体的适应度，Ri 是第i个个体的适应度排名，N 是种群个体数。遗传原型中使用的是轮盘法，但该方法除了计算快之外缺点太多，故推荐使用排名法。即适应度排名越靠后，其被淘汰的几率越高。

代码如下：

clear
clc
close all

f = @(x) sin(x) + x .* cos(x);   % 函数表达式
ezplot(f, [0, 2*pi])             % 画出函数图像

N = 50;                          % 种群上限
ger = 100;                       % 迭代次数
L = 5;                           % 基因长度
pc = 0.8;                        % 交叉概率
pm = 0.1;                        % 变异概率
dco = [10000; 1000; 100; 10 ;1]; % 解码器
dna = randi([0, 9], [N, L]);     % 基因
hold on
x = dna * dco / 99999 * 2 * pi;  % 对初始种群解码
plot(x, f(x),'ko','linewidth',3) % 画出初始解的位置

x1 = zeros(N, L);                % 初始化子代基因，提速用
x2 = x1;                         % 同上
x3 = x1;                         % 同上
fi = zeros(N, 1);                % 初始化适应度，提速

for epoch = 1: ger               % 进化代数为100
    for i = 1: N                 % 交叉操作
        if rand < pc
           d = randi(N);            % 确定另一个交叉的个体
           m = dna(d,:);            % 确定另一个交叉的个体
           d = randi(L-1);          % 确定交叉断点
           x1(i,:) = [dna(i,1:d), m(d+1:L)];  % 新个体 1        
           x2(i,:) = [m(1:d), dna(i,d+1:L)];  % 新个体 2
        end
    end
    x3 = dna;
    for i = 1: N                           % 变异操作
        if rand < pm
            x3(i,randi(L)) = randi([0, 9]);
        end
    end
    dna = [dna; x1; x2; x3];               % 合并新旧基因
    fi = f(dna * dco / 99999 * 2 * pi);    % 计算适应度，容易理解
    dna = [dna, fi];
    dna = flipud(sortrows(dna, L + 1));    % 对适应度进行排名
    while size(dna, 1) > N                 % 自然选择
        d = randi(size(dna, 1));           % 排名法
        if rand < (d - 1) / size(dna, 1)
            dna(d,:) = [];
            fi(d, :) = [];
        end
    end
    dna = dna(:, 1:L);
end
x = dna * dco / 99999 * 2 * pi;            % 对最终种群解码
plot(x, f(x),'ro','linewidth',3)           % 画出最终解的位置
disp(['最优解为x=',num2str(x(1))]);
disp(['最优值为y=',num2str(fi(1))]);