BP神经网络解决相关问题

利用BP神经网络工具箱解决分类的问题

BP介绍

BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络。

基本BP算法包括信号的前向传播和误差的反向传播两个过程。即计算误差输出时按从输入到输出的方向进行，而调整权值和阈值则从输出到输入的方向进行。

正向传播时，输入信号通过隐含层作用于输出节点，经过非线性变换，产生输出信号，若实际输出与期望输出不相符，则转入误差的反向传播过程。

误差反传是将输出误差通过隐含层向输入层逐层反传，并将误差分摊给各层所有单元，以从各层获得的误差信号作为调整各单元权值的依据。

通过调整输入节点与隐层节点的联接强度和隐层节点与输出节点的联接强度以及阈值，使误差沿梯度方向下降，经过反复学习训练，确定与最小误差相对应的网络参数(权值和阈值)，训练即告停止。此时经过训练的神经网络即能对类似样本的输入信息，自行处理输出误差最小的经过非线形转换的信息。

优点

BP神经网络无论在网络理论还是在性能方面已比较成熟。其突出优点就是具有很强的非线性映射能力和柔性的网络结构。网络的中间层数、各层的神经元个数可根据具体情况任意设定，并且随着结构的差异其性能也有所不同。

缺点

1.学习速度慢，即使是一个简单的问题，一般也需要几百次甚至上千次的学习才能收敛；
2.容易陷入局部极小值；
3.网络层数、神经元个数的选择没有相应的理论指导（神经元个数可大概根据公式计算得到）；
4.网络推广能力有限

1.BP神经网络解决线性拟合问题

未知样本数据，根据公式计算相应y的值组为一个行向量；设定训练次数和精度。再选择相应的神经网络结构进行计算。

 x = [0:0.03:4]; %训练数据输入值
x1 = [0:0.06:4]; %预测数据输入值
y = cos(4*pi*x) + sin((4*pi*x)/3); %训练数据输出值

[X,minx,maxx,Y,miny,maxy]=premnmx(x,y); %对x、y归一化处理
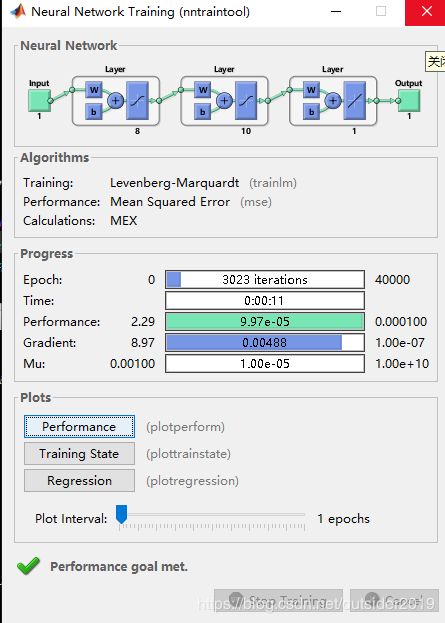
s = [8,10,1]; %影藏层、输出层数目
net=newff(minmax(x),s,{'tansig','tansig','purelin'},'trainlm');
net.trainParam.epochs = 40000;%训练次数
 net.trainParam.goal = 0.0001;%训练精度
 net.trainParam.lr=0.1;
 net=train(net,X,Y);%神经网络训练

 
 x2=premnmx(x1);%将x1进行归一化处理
 b = sim(net,x2);%得到预测（检验）数据输出值
 B = postmnmx(b,miny,maxy);%将得到的数据输出值反归一化得到预测（检验）数据
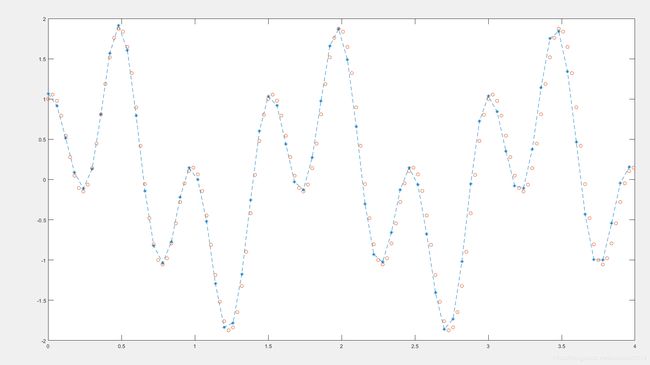
 plot(x1,B,'--*',x,y,'o');

巡行结果如下：

通过这样的方式可以实现蝇分类、运动员数据的预测等问题！

2.BP神经网络工具解决预测问题

成绩预测：通过已知数据预测某一特征值。

P=[3.2 3.2 3 3.2 3.2 3.4 3.2 3 3.2 3.2 3.2 3.9 3.1 3.2;
9.6 10.3 9 10.3 10.1 10 9.6 9 9.6 9.2 9.5 9 9.5 9.7;
3.45 3.75 3.5 3.65 3.5 3.4 3.55 3.5 3.55 3.5 3.4 3.1 3.6 3.45;
2.15 2.2 2.2 2.2 2 2.15 2.14 2.1 2.1 2.1 2.15 2 2.1 2.15;
140 120 140 150 80 130 130 100 130 140 115 80 90 130;
2.8 3.4 3.5 2.8 1.5 3.2 3.5 1.8 3.5 2.5 2.8 2.2 2.7 4.6;
11 10.9 11.4 10.8 11.3 11.5 11.8 11.3 11.8 11 11.9 13 11.1 10.85;
50 70 50 80 50 60 65 40 65 50 50 50 70 70];
T=[2.24 2.33 2.24 2.32 2.2 2.27 2.2 2.26 2.2 2.24 2.24 2.2 2.2 2.35];

[p1,minp,maxp,t1,mint,maxt]=premnmx(P,T);

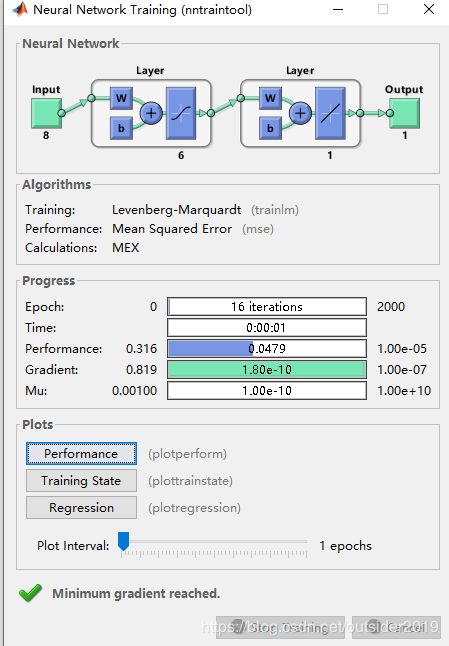
s=[6,1];
net=newff(minmax(P),s,{'tansig','purelin'},'trainlm');

net.trainParam.lr=0.05;
net.trainParam.epochs=2000;
net.trainParam.goal=0.00001;
net=train(net,p1,t1);
a = [3.0;9.3;3.3;2.05;100;2.8;11.2;50];
w = [3.2;9.6;3.45;2.15;140;2.8;11;50];
a=premnmx(a);
w = premnmx(w);
A=sim(net,a);
W=sim(net,w);

A=postmnmx(A,mint,maxt)
W=postmnmx(W,mint,maxt)

运行结果如下：

A =

       2.2143


W =

       2.2143

从结果来看，有较好的预测效果。

3.代码实现BP神经网络工具箱（字符分类问题）

（1）激励函数为：y = (exp(x)-exp(-x))/(exp(x)+exp(-x))

这个函数实现的是将数据变换为在【-1，1】内，效果优于下面介绍的第二种激励函数！

代码如下：

1）样本数据配置

clc,clear
I = [0 1 0 0 1 0 0 1 0]';
 T = [1 1 1 0 1 0 0 1 0]';
U = [1 0 1 1 0 1 1 1 1]';
trainNumber=3;
testNumber=1

trainData =  [0 1 1;1 1 0;0 1 1;0 0 1;1 1 0;0 0 1;0 0 1;1 1 1;0 0 1;
              1 -1 -1;
              -1 1 -1;
              -1 -1 1];%训练样本;
testData = T;%测试数据;

2）设置输入层、隐藏层、输出层

hideSize=6;%隐含层神经元数目(5——14)
outSize=3;%输出层神经元数目
inSize=9;%输入层神经元数目

3）设置学习率、权重与阈值

Learning = 0.001;%学习率
W1=rand(hideSize,inSize);%输入层到隐含层之间的权重
W2=rand(outSize,hideSize);%隐含层到输出层之间的权重
B1=rand(hideSize,1);%隐含层神经元的阈值
B2=rand(outSize,1);%输出层神经元的阈值

4）前向传播
设置好训练次数，将样本数据数据进行训练

Falses=80000;%训练次数 
E=zeros(1,Falses);
for False=1:Falses
    for sample=1:trainNumber
        x =trainData(1:9,sample);%取训练样本的前两行，每次取1列
        hide_in=W1*x+B1;%影藏层输入值
        hide_out = zeros(hideSize,1);%隐含层输出值
        for j=1:hideSize
        hide_out(j)=tanhhh(hide_in(j));
        end

        y_in=W2*hide_out+B2;%输入层输入值
        y_out = zeros(outSize,1);%输出层输出值
        for j=1:outSize
		y_out(j)=tanhhh(y_in(j));
        end
        %求误差
        e=y_out-Y(:,sample);%输出层计算结果误差（实际输出-期望输出）
        E = 0;
        for i=1:outSize
        E = E+e(i);
        end

5）后向反馈
分别计算各权重的变化量

dW2(j,k)=Learning*e(j)*hide_out(k)*tanhhh(y_in(j))*(1-tanhhh(y_in(j)));
Sum=Sum+e(m)*Learning*x(k)*tanhhh(y_in(m))*(1-tanhhh(y_in(m)))*tanhhh(hide_in(j))*(1-tanhhh(hide_in(j)))*W2(m,j);
Sum2 = Sum2 + tanhhh(y_in(k))*(1-tanhhh(y_in(k)))*W2(k,j)*tanhhh(hide_in(j))*(1-tanhhh(hide_in(j)))*e(k)*Learning;

6）得到新的权值与阈值

W1=W1-dW1;
	W2=W2-dW2;

	B1=B1-dB1;
	B2=B2-dB2;

再将检验数据放入网络中，即可得到相应的结果

inspect_out = zeros(outSize,testNumber);
for i = 1:testNumber
    x = testData(1:9,i);
    
    hide_in = W1*x+B1;%隐含层输入值
    hide_out = zeros(hideSize,1);%隐含层输出值
    for j = 1:hideSize
        hide_out(j) = tanhhh(hide_in(j));
    end
    
    Y_in = W2*hide_out+B2;%输出层输入值
    Y_out = zeros(outSize,1);
    for j = 1:outSize
       Y_out(j) = tanhhh(Y_in(j));
    end
    inspect_out(:,i) = Y_out

结果如下：

A1 =

       0.9992
     -0.99889
      -1.0005

可以看出，结果与本应该出现的结果有偏差。但是在神经网络中，“逼近“是一个模糊的感念，表示的是实际输出与期望输出的接近程度。

（2）激励函数为y = 1/(1+exp(-x));

这个函数实现的是将数据变换为在【0，1】内，有一定的局限性！
故将上面的样本数据的期望输出的-1修改为0代替！

1）相关配置如下：

hideSize=12;%隐含层神经元数目(5——13)
outSize=3;%输出层神经元数目
inSize=9;%输入层神经元数目
Learning = 0.05;%学习率

其他代码与上一个激励函数的代码相同
结果如下：

      0.0061506
      0.017364
      0.98049

相比较而言，这个结果与期望数据更为逼近。