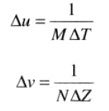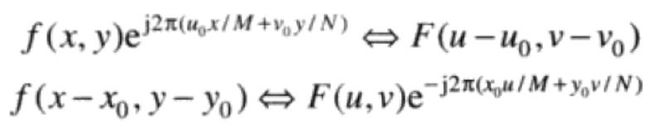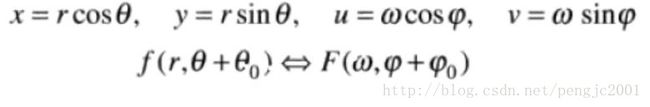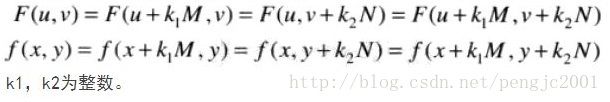频率域滤波基础之一(读数字图像处理学习halcon)
如果不了解在图像滤波中如何应用傅里叶变换和频率域的基本知识,要彻底理解这一领域也是不太可能。
二维离散傅里叶变换的一些性质
1、空间和频率间隔的关系
假设对连续函数f(t,z)取样生成了一副数字图像f(x,y),它由分别在t和z方向所取的MxN个样点组成。令△T和△Z表示样本间的间隔。那么相应离散频率域变量间的间隔分别由
2、平移和旋转
用指数项乘以f(x,y)将使DFT的原点移动到点(u0,v0);反之,用负指数乘以F(u,v)将使f(x,y)的原点移动到点(x0,y0)。平移不影响F(u,v)的幅度(谱)。
使用极坐标则
说明,若f(x,y)旋转θ0角度,则F(u,v)也旋转相同的角度。同理,F(u,v)旋转一个角度,f(x,y)也旋转相同角度。
3、周期性
4、对称性
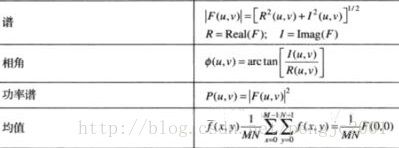
5、傅立叶谱和相角
注:因为比例常数MN通常很大,典型地,|F(0,0)|是谱的最大分量,它可能比其他项大几个数量级。因为原点处的频率分量u和v是0,所以F(0,0)有时称为直流(dc)分量。
Halcon相关算子解析
求取图像的傅立叶变换图
fft_generic(Image : ImageFFT : Direction, Exponent, Norm, Mode, ResultType : )
fft_image(Image : ImageFFT : : ) fft_generic(Image,ImageFFT,'to_freq',-1,'sqrt','dc_center','complex')
求取功率谱
power_byte(Image : PowerByte : : )
power_ln(Image : ImageResult : : )
power_real(Image : ImageResult : : )
求相位角
phase_deg(ImageComplex : ImagePhase : : )
phase_rad(ImageComplex : ImagePhase : : )
构建一幅512x512的背景为黑色的图像,其中有一128x256的白色区域。F(0,0)我们很容易得到是8355840。
read_image (Image, 'D:/halcon work/fft/512x512-1.bmp')
rgb1_to_gray (Image, GrayImage)
fft_generic (GrayImage, ImageFFT, 'to_freq', -1, 'none', 'dc_center', 'complex')
power_real (ImageFFT, ImageResult)
phase_deg (ImageFFT, ImagePhase)
read_image (Image1, 'D:/halcon work/fft/512x512 - 2.bmp')
rgb1_to_gray (Image1, GrayImage1)
fft_generic (GrayImage1, ImageFFT1, 'to_freq', -1, 'none', 'dc_center', 'complex')
power_real (ImageFFT1, ImageResult1)
phase_deg (ImageFFT1, ImagePhase1)
read_image (Image2, 'D:/halcon work/fft/512x512 - 3.bmp')rgb1_to_gray (Image2, GrayImage2)fft_generic (GrayImage2, ImageFFT2, 'to_freq', -1, 'none', 'dc_center', 'complex')power_real (ImageFFT2, ImageResult2)
phase_deg (ImageFFT2, ImagePhase2)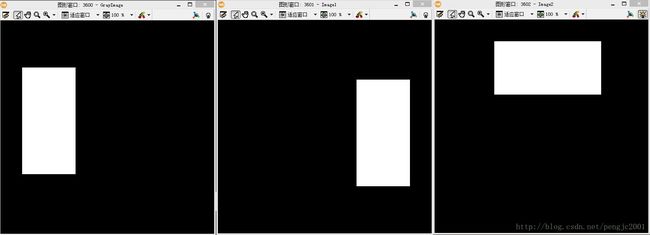
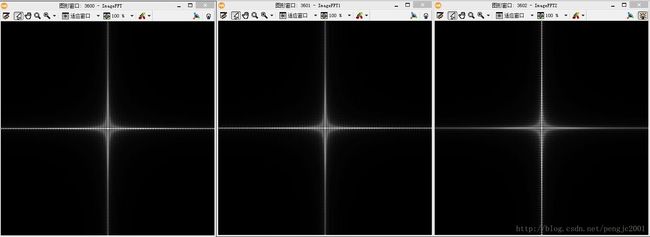
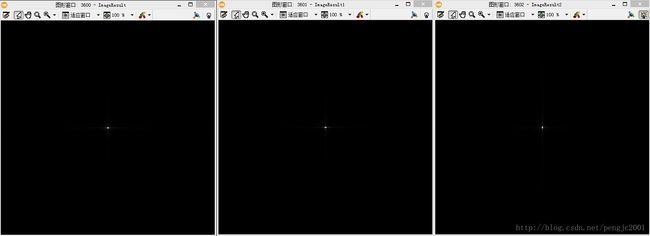
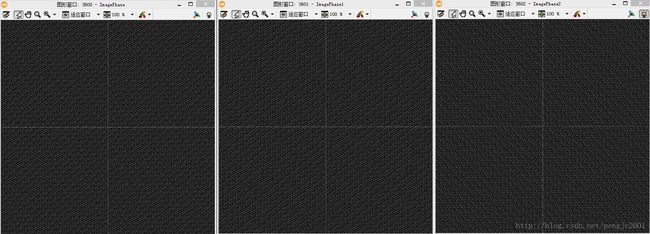
从上面的结果可以看出
1、在傅立叶转换的图像中,长度方向要比宽度方向密集
2、平移、旋转不影响功率谱图,旋转影响傅立叶变换图、相位图、功率谱图。
3、直流分量=图像平均灰度X面积。