Dijkstra算法、prim算法和 Kruskal算法详解

1 Dijkstra算法

问题描述：在一个图中，给定指定顶点，求该顶点到其它顶点的最短距离。

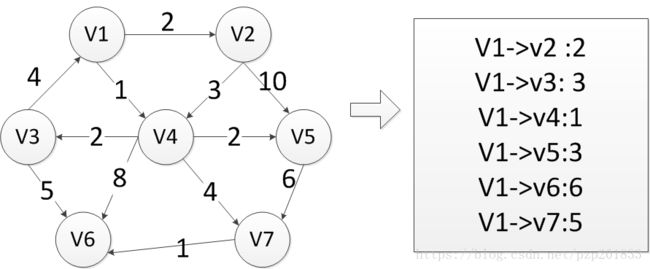
如图所示：这是一个有向图，现在要求解从顶点V1到其它顶点的最短距离。以上图为例，利用Dijkstra算法求解最短距离。

步骤：

（1）将所有顶点分为两组，一组是未知的即为S,一组是已知的记为W。开始时，S={V1,V2,V3,V4,V5,V6,V7},W={};

(2)首先选择顶点V1到其它顶点中距离最短的顶点为已知顶点。显然V1->v1=0为最小值。这时S={V2,V3,V4,V5,V6,V7},W={V1};

更新距离表格：

（3）接着在已知的距离中，v1->v4的距离最短，将顶点4放入已知的序列中。这时S={V2,V3,V5,V6,V7},W={V1，V4},更新距离表格。

（4） 重复上述过程，在未知顶点中，选择距离最小的作为已知的，V1->V2=2是最小的，选择V2作为已知的。此时，S={V3,V5,V6,V7},W={V1，V4，V2},更新距离。

（5）重复上述过程，分别是V5和V3被选为已知的，此时，S={V6,V7},W={V1，V4，V2,V5，V3}。更新距离表格后得到：

（6）比较可知，选择V7作为已知的，此时，S={V6},W={V1，V4，V2,V5，V3，V7}。更新距离表格后得到：

（7）最后选择V6,更新距离，算法结束。最终结果如下图所示：

具体代码如下：

void Dijkstra(const vector>& path, vector& flag,vector& res,int v)
{
    const int n=flag.size();
    for(int i=0;i

2 prim算法

计算最小生成树采用prim算法。在每一步，将节点当做根并往上加边，将相关顶点增加到增长的树上。在算法的每一个阶段都可以通过选择边（u,v）,使得（u,v）的值是所有u在树上但v不在树上的边的值的最小者，从而找到一个新的顶点并将它添加到这棵树中。

代码如下：

void prim(const vector>& path, vector& flag,vector& res,int v)
{
    const int n=flag.size();
    for(int i=0;i

3 kruskal算法

和prim算法类似，每次都是寻找权值最短的一条边。可以这样看：开始存在n颗单节点树，每次找到权值最短的一棵树将其合并起来，但是注意不要形成环。最后只剩下一棵树的时候，代表合并完成。

代码如下：

                                                                                                                               

bool cmp(pair,int> a,pair,int> b)
{
    return a.second<=b.second;
}
bool isSame(vector,bool>>& flag,pair t)
{
    int x=t.first;
    int y=t.second;
    for(int i=x+1;i)!=flag.end()&&flag.find(make_pair)!=flag.end())
        {
            return true;
        }
    }
    return false;
}
void krustral(const vector>& path,vector,bool>>& flag,vector& res)
{
    const int n=flag.size();
    vector,int>> m;
    for(int i=0;i