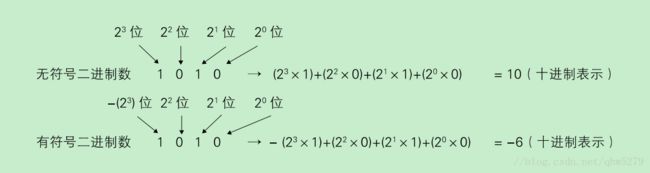补码在二进制带符号运算中的应用
1. 引入补码的原因
在数字电路或系统中,为简化电路,常将负数用补码表示,以便将减法运算变为加法运算。
以钟表为例,时间从6点钟减少到2点钟,可以通过6-4=2逆时针转动4个小时实现;也可以通过6+8=14(表盘为12进制,满12部分舍去,所以14表示的即为2点)顺时针转动8个小时实现同样效果。所以在表盘上,-4与+8具有同样的效果。故对于-4而言,+8称为它在以12为“模”时的补数。也就是说负数(-X)的补数=模-X的绝对值|X|。所以当模为12时,-4的补码=12-4=8。
数电课本中提到二进制数的补码表示方式:
若基数为,位数为的原码,其补码为
N补=R^n-|N|
这与负数(-X)的补数=模-X的绝对值|X|是一致的。在二进制带符号运算中,求负数补码时会用到对原码取反加1的操作。以-3为例,下面将按照上述公式,用4位二进制数表示该数字的补码。
-3的绝对值为3,对应4位二进制数为0011;模为16=1111+1。所以
-3补 = (1111+1)-0011= (1111-0011)+1
其中(1111-0011)这一步就是对0011按位取反,所以-3补=|-3|按位取反加1。
2. 无符号数和有符号数表示范围
以4位二进制数为例,当表示无符号数时,所表示范围为0000~1111,对应十进制中的0D~15D,共计16个数。
当表示有符号数时,最高位为符号位,0表示正数,1表示负数。所表示范围0000~1111对应十进制中的-8~7,也是16个数。
在数电课本中曾提到:
当二进制数为正数时,其反码、补码和原码相同。
当二进制数为负数时,保持最高为符号位不变,将数值位按位求反(得到反码),然后在最低位加1得到补码。
3.为什么符号位能参与运算?
如图1所示,一个4位二进制数所能表示范围类似于一个圆。图中红色二进制数表示的是各数字所对应的补码,即参与真实运算时的代码。从0000到1111,随着补码值的增长,对应十进制数依次为0,1,2,3,4,5,6,7,-8,-7,-6,-5,-4,-3,-2,-1,共计16个数。也就是说补码能按照从0000~1111自然增长的方式,去决定-8~7之间数字在“圆型表盘”上的位置。以0-3为例,可以看做逆时针减去3个数;也可以看做顺时针加上13个数,而这个13所对应的二进制数1101就是-3的补码,这里就将0-3的减法转换成了0+13的加法。最后一步就是将补码13(1101)转换为相应的原码:-3(1011).具体转换方式见问题5回答。
4. 为什么负数在求补码时符号位要保持不变,其余位求反加1?
在图1所示的圆中,以0(0000)和-8(1000)为界分为了两个半圆。其中一半是0~7共计8个数,它们的共同点是最高位都为0;另一半是-8~-1,它们的共同点是最高位都为1。
对于0~7,其计数规律符合人的使用习惯,这里不再表述。而对于-8~-1,最高位为1一方面说明它们都是负数;另一方面说明这些值在实际计算中,已经在“表盘上”多走了半圈。也就是说减去一个数x,相当于在加8基础上再加上(8-|x|)。所以对于4位二进制表示的负数,原码转补码过程就是:符号位不变(最高位表示的半圈——加8),其余位置取反加1(余下三位二进制表示的模为8,取反加1就是执行8-|x|)。
5. 为什么运算完的结果还要再转为原码?
在不超限溢出的前提下,如果计算结果为正数,那么补码与原码相同,得到的就是正确结果;如果计算结果为负数,还需要将补码再转换成原码。仍以0-3为例,在图1中,-3所对应补码为1101,如果不加处理,1101对应的将是-5,抛开最高位的负号不看,显然3跟5是关于低三位的模8是互为补数的。也就是说对于-3,已知补码为1101后,保持最高位不变,低三位取反加1(即低三位求补),就能得到对应的原码1011(机器求原码的方法)。同样的-7的补码对应-1,-6的补码对应-2……也符合这样的规律,具体见表一中负数的补码和对应十进制数之间的关系。故计算完得到补码后,仍要转为原码。另附一种已知补码,简单计算原码的方法,如图3所示(人求原码的方法),其基本原理参考图1即可。对于计算中出现的溢出问题,见图3,溢出会造成错误计算结果,是要着力避免的。
表一 4位二进制数原码、反码、补码对照表
正数(正数的原码=反码=补码) |
负数 |
||||
二进制 |
十进制 |
二进制原码 |
二进制反码 |
二进制补码 |
十进制 |
0000 |
0 |
— |
— |
1000(-0D) |
-8 |
0001 |
1 |
1001 |
1110 |
1111(-7D) |
-1 |
0010 |
2 |
1010 |
1101 |
1110(-6D) |
-2 |
0011 |
3 |
1011 |
1100 |
1101(-5D) |
-3 |
0100 |
4 |
1100 |
1011 |
1100(-4D) |
-4 |
0101 |
5 |
1101 |
1010 |
1011(-3D) |
-5 |
0110 |
6 |
1110 |
1001 |
1010(-2D) |
-6 |
0111 |
7 |
1111 |
1000 |
1001(-1D) |
-7 |
图1 四位二进制数表示范围示意图
图2 有符号数已知补码求原码方法
图3 溢出问题
本文参考文献:
[1] 康华光. 电子技术基础数字部分(第六版)[M]. 高等教育出版社, 2013.
[2] 水头一寿, 米泽辽, 藤田裕士,等. CPU自制入门[J]. 2014.