四叉树的C++实现

四叉树的数据结构
抽象数据类型定义如下：

ADT QuadTrees{
	数据对象D：D是具有相同性质的具有二维结构的数据元素的集合,本实验为坐标数据。
	数据关系R：若D为空集，则称为空树；若D仅含有一个数据元素，则R为空集，否则R={H}，	H是如下二元关系：
	(1) 在D中存在唯一的元素root，它在关系H下无父节点；
	(2) D中任意元素d将其子节点划分为四个象限，将其直接相邻的节点分别设为d[1],d[2],d[3],d[4]；
	(3) 若D-{root}≠ɸ，则存在D-{root} ={root[1],root[2],root[3],root[4]}，且两两无交集；
	(4) 若d[i] ≠ɸ(i=1,2,3,4),则d[i]中存在唯一的xi ，<root, xi> ∈H，且存在d[i]上的关系Hi⊂H；
	       H={<root, xi>, Hi},i=1,2,3,4;
	(5) (root[i],{Hi})i=1,2,3,4 是符合定义的四叉树;
	基本操作：
	QuadTreeInit(QT);//构造空的四叉树
	Compare(node A, node B);//返回B在A的第几个象限，返回值取之只能为1,2,3,4
	StaightforwardInsertion(QT,K);//简单插入节点K(不考虑树的平衡)
	SophisticatedInsertion(QT,K);//插入节点K(考虑树的平衡)
	RegionSearch(QT,K,double L,R,B,T);//查找节点K所有在x=L,x=B,y=R,y=T所构成矩形区域的子节点
	}ADT QuadTrees;

算法实现
四叉树给出如下定义：
一棵四叉树T是由一个或一个以上节点组成的有限集，其中有一个特定的节点R称为T的根节点。如果集合( T - { R } ) 非空，那么集合中的这些点被划分为n(n≤4)个不相交的子集 ，其中每个子集都是四叉树,并且其相应的根节点 是R的子节点。子集 称为T 的子树。
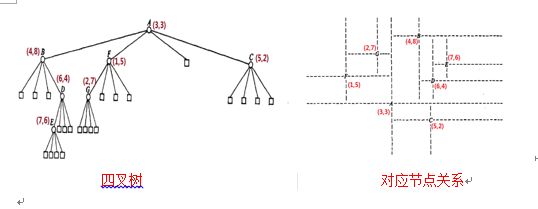
四叉树与对应节点关系：

以下是源码：

#include 
#include 
using namespace std;

template
struct Point{
	T x;
	T y;
	Point(){}
	Point(T _x, T _y) :x(_x), y(_y){}
};

template
struct Node{
	Node* R[4];
	Point pt;
	Node* parent;
};

template
class QuardTree
{
public:
	QuardTree();
	~QuardTree();
	void Insert(const Point& pos);
	void BalanceInsert(const Point& pos );
	int nodeCount();
	int TPLS();
	int Height();
	void RegionResearch(ElemType left, ElemType right, ElemType botom, ElemType top, int& visitednum,int& foundnum);
	void clear();
private:
	Node* root;
	int Compare(const Node* node, const Point& pos);
	bool In_Region(Point t, ElemType left, ElemType right, ElemType botom, ElemType top);
	bool Rectangle_Overlapse_Region(ElemType L, ElemType R, ElemType B, ElemType T, ElemType left, ElemType right, ElemType botom, ElemType top);
	void RegionResearch(Node* t, ElemType left, ElemType right, ElemType botom, ElemType top, int& visitednum, int& foundnum);
	int Depth(Node* &);
	int nodeCount(const Node*);
	void clear(Node < ElemType>*& p);
	void Insert(Node*& , const Point& pos);//递归插入节点
};


template
QuardTree::QuardTree()
{
	root = NULL;
}

template
QuardTree::~QuardTree()
{
	clear(root);
}

template
int QuardTree::TPLS()
{
	return Depth(root);
}

template
int QuardTree::Compare(const Node* node, const Point& pos)
{
	if (pos.x == node->pt.x && pos.y == node->pt.y) return 0;
	if (pos.x >= node->pt.x && pos.y>node->pt.y)  return 1;
	if (pos.xpt.x  && pos.y >= node->pt.y) return 2;
	if (pos.x <= node->pt.x && pos.ypt.y)  return 3;
	if (pos.x>node->pt.x  && pos.y <= node->pt.y) return 4;
	return -1;
}


template
void QuardTree::BalanceInsert(const Point& pos)
{
	Node* node = (Node*)malloc(sizeof(Node));
	node->R[0] = NULL;
	node->R[1] = NULL;
	node->R[2] = NULL;
	node->R[3] = NULL;
	node->parent = NULL;
	node->pt = pos;
	if (root == NULL)
	{
		root = node;
		return;
	}
	Node* temp = root;
	int direction = Compare(temp, pos);
	if (direction == 0) return;
	while (temp->R[direction - 1] != NULL)
	{
		temp = temp->R[direction - 1];
		direction = Compare(temp, pos);
		if (direction == 0) return;
	}
	temp->R[direction - 1] = node;
	node->parent = temp;
	
	Node* tp = temp->parent;
	if (tp == NULL) return;
	int r = Compare(tp, temp->pt);

	if (abs(direction-r) == 2)
	{
		Node* leaf = node;
		if (tp->R[abs(3 - r)] == NULL )
		{
			tp->R[r - 1] = NULL;
			temp->parent = leaf;
			leaf->R[r-1] = temp;

			temp->R[abs(3 - r)] = NULL;
			Node* Rt = tp->parent;
			if (Rt == NULL)
			{
				root = leaf;
				leaf->parent = NULL;

				leaf->R[abs(3 - r)] = tp;
				tp->parent = leaf;
				return;
			}
			tp->parent = NULL;
			int dd = Compare(Rt, tp->pt);

			Rt->R[dd - 1] = leaf;
			leaf->parent = Rt;

			leaf->R[abs(3 - r)] = tp;
			tp->parent = leaf;
		}
	}	
}


template
void QuardTree::Insert(Node*& p, const Point& pos)
{
	if (p == NULL)
	{
		Node* node = (Node*)malloc(sizeof(Node));
		node->R[0] = NULL;
		node->R[1] = NULL;
		node->R[2] = NULL;
		node->R[3] = NULL;
		node->pt = pos;
		p = node;
		return;
	}
	else
	{
		int d = Compare(p, pos);
		if (d == 0) return;
		Insert(p->R[d - 1], pos);
	}
}


template
void QuardTree::Insert(const Point& pos)
{
	int direction, len = 0;
	Node* node = (Node*)malloc(sizeof(Node));
	node->R[0] = NULL;
	node->R[1] = NULL;
	node->R[2] = NULL;
	node->R[3] = NULL;
	node->pt = pos;
	if (root == NULL)
	{
		root = node;
		return;
	}
	direction = Compare(root, pos);
	Node* temp = root;
	if (direction == 0) return;//节点已存在 
	len = 1;
	while (temp->R[direction - 1] != NULL)
	{
		temp = temp->R[direction - 1];
		direction = Compare(temp, pos);
		if (direction == 0) return;
	}
	temp->R[direction - 1] = node;
	//Insert(root, pos);//递归插入节点
}





template
int QuardTree::nodeCount()
{
	return nodeCount(root);
}

template
int QuardTree::nodeCount(const Node* node)
{
	if (node == NULL) return 0;
	return 1 + nodeCount(node->R[0]) + nodeCount(node->R[1]) + nodeCount(node->R[2]) + nodeCount(node->R[3]);
}

template
bool QuardTree::In_Region(Point t, T left, T right, T botom, T top)
{
	return t.x >= left && t.x <= right && t.y >= botom && t.y <= top;
}

template
bool QuardTree::Rectangle_Overlapse_Region(ElemType L, ElemType R, ElemType B, ElemType T, 
	ElemType left, ElemType right, ElemType botom, ElemType top)
{
	return L <= right && R >= left && B <= top && T >= botom;
	//return true;
}//优化查找速度

template
void QuardTree::RegionResearch(Node* t, T left, T right, T botom, T top, int& visitednum, int& foundnum)
{
	if (t == NULL) return;
	T xc = t->pt.x;
	T yc = t->pt.y;
	if (In_Region(t->pt, left, right, botom, top)){ ++foundnum; }
	if (t->R[0] != NULL && Rectangle_Overlapse_Region(xc, right, yc, top, left, right, botom, top))
	{
		visitednum++;
		RegionResearch(t->R[0], xc>left?xc:left, right, yc>botom?yc:botom, top, visitednum, foundnum);
	}
	if (t->R[1] != NULL && Rectangle_Overlapse_Region(left, xc, yc, top, left, right, botom, top))
	{
		visitednum++;
		RegionResearch(t->R[1], left, xc>right?right:xc, yc>botom?yc:botom, top, visitednum, foundnum);
	}
	if (t->R[2] != NULL && Rectangle_Overlapse_Region(left, xc, botom, yc, left, right, botom, top))
	{
		visitednum++;
		RegionResearch(t->R[2], left, xcR[3] != NULL && Rectangle_Overlapse_Region(xc, right, botom, yc, left, right, botom, top))
	{
		visitednum++;
		RegionResearch(t->R[3], xc>left ? xc : left, right, botom, yc
void QuardTree::clear()
{
	clear(root);
}

template
void QuardTree::clear(Node* &p)
{
	if (p == NULL) return;
	if (p->R[0]) clear(p->R[0]);
	if (p->R[1]) clear(p->R[1]);
	if (p->R[2]) clear(p->R[2]);
	if (p->R[3]) clear(p->R[3]);
	free(p);
	p = NULL;
}

template
void QuardTree::RegionResearch(T left, T right, T botom, T top, int& visitednum, int& foundnum)
{
	RegionResearch(root, left, right, botom, top, visitednum,foundnum);
}

template
int QuardTree::Depth(Node* &node)
{
	if (node == NULL) return 0;
	int dep = 0;
	Node* tp = root;
	while (tp->pt.x!=node->pt.x || tp->pt.y!=node->pt.y)
	{
		dep++;
		tp = tp->R[Compare(tp, node->pt) - 1];
		if (tp == NULL) break;
	}
	return dep + Depth(node->R[0]) + Depth(node->R[1]) + Depth(node->R[2]) + Depth(node->R[3]);
}

参考文献
Finkel R A, Bentley J L. Quad trees a data structure for retrieval on composite keys[J]. Acta Informatica, 1974, 4(1):1-9.