编程入门09：Python字典类型

上一篇：编程入门08：Python列表类型

现在让我们来学习另一种复合数据类型“字典”（dict）——字典是用花括号括起来的“键值对”（Key-value pair），键和值之间用冒号分隔，键值对之间用逗号分隔。键在一个字典中具有唯一性，其作用就相当于序列中的索引号——与索引号只能是整数不同，任何不可变对象都能作为键（通常会使用字符串），字典类型不属于序列而是属于“映射”（Mapping）。字典与列表一样是可变对象，你可以用赋值的方式直接修改元素，而且字典还允许给原本不存在的键赋值，即添加新元素：

In [1]: d1 = {"010":"北京", "021":"上海", "022":"天津"}

In [2]: d1["021"]
Out[2]: '上海'

In [3]: d1["020"] = "广州"

In [4]: d1
Out[4]: {'010': '北京', '020': '广州', '021': '上海', '022': '天津'}

字典也支持迭代，字典直接用来迭代取到的是键，字典提供三个专门方法keys()、values()、items()分别返回键、值或键值对的序列：

In [5]: list(d1)  # 字典直接转列表只保留键
Out[5]: ['010', '021', '022', '020']

In [6]: d1.keys()
Out[6]: dict_keys(['010', '021', '022', '020'])

In [7]: d1.values()
Out[7]: dict_values(['北京', '上海', '天津', '广州'])

In [8]: d1.items()  # 此方法返回序列中的元素是元组
Out[8]: dict_items([('010', '北京'), ('021', '上海'), ('022', '天津'), ('020', '广州')])

In [9]: for k, v in d1.items():  # 字典元素的迭代循环
   ...:     print("{}: {}".format(k, v))
   ...:     
010: 北京
021: 上海
022: 天津
020: 广州

字典名加方括号指定键可以返回元素的值，但如果指定的键不存在就会发生错误，因此推荐使用专门的get()方法来取值（当键不存在时返回None或是指定的默认值）；字典还提供专门的setdefault()方法用于元素初始赋值（当键不存在时添加键并赋指定的默认值，否则保持原值不变）。

In [10]: d1.get("023", "无")
Out[10]: '无'

In [11]: d1.setdefault("023", "重庆")
Out[11]: '重庆'

In [12]: d1
Out[12]: {'010': '北京', '020': '广州', '021': '上海', '022': '天津', '023': '重庆'}

In [13]: d1.setdefault("023", "重庆市")
Out[13]: '重庆'

In [14]: d1
Out[14]: {'010': '北京', '020': '广州', '021': '上海', '022': '天津', '023': '重庆'}

In [15]: txt = "Good good study, day day up!"  # 这段代码统计文本中每个字符的出现次数
    ...: d2 = {}  # IPython一次交互允许输入多条语句（按Ctrl+Enter换行）
    ...: for c in txt:
    ...:     d2.setdefault(c, 0)
    ...:     d2[c] += 1
    ...: print(sorted(d2.items(), key=lambda i:i[1], reverse=True))  # 序列按元素值降序排列
    ...: 
[('d', 5), (' ', 5), ('o', 4), ('y', 3), ('u', 2), ('a', 2), ('G', 1), ('g', 1), ('s', 1), ('t', 1), (',', 1), ('p', 1), ('!', 1)]

上面最后一段代码中实现排序功能的sorted函数用key参数指定一个函数对象作为排序依据，本例使用lambda关键字定义了一个“匿名函数”，其写法为lambda 参数:返回值——匿名函数作为参数相比完整的函数声明更简单也更清晰。

如果用花括号括起来的不是键值对而是单一对象，就定义了一个“集合”（Set）——注意“{}”是空字典，定义空集合要使用集合“构造器”set()。Python集合类型就相当于数学中的集合概念，集合中的元素是无序的，可以进行“交”（&）“并”（|）“差”（-）和“对称差”（^）等集合运算，在编程中常会把列表和元组等对象转为集合来去除重复的元素。

In [16]: {1, 2, 3, 4} & {3, 4, 5, 6}  # 交集
Out[16]: {3, 4}

In [17]: {1, 2, 3, 4} | {3, 4, 5, 6}  # 并集
Out[17]: {1, 2, 3, 4, 5, 6}

In [18]: {1, 2, 3, 4} - {2, 3}  # 差集
Out[18]: {1, 4}

In [19]: {1, 2, 3, 4} ^ {3, 4, 5, 6}  # 对称差集
Out[19]: {1, 2, 5, 6}

In [20]: set(txt.split())  # 字符串拆成列表再转为集合
Out[20]: {'Good', 'day', 'good', 'study,', 'up!'}

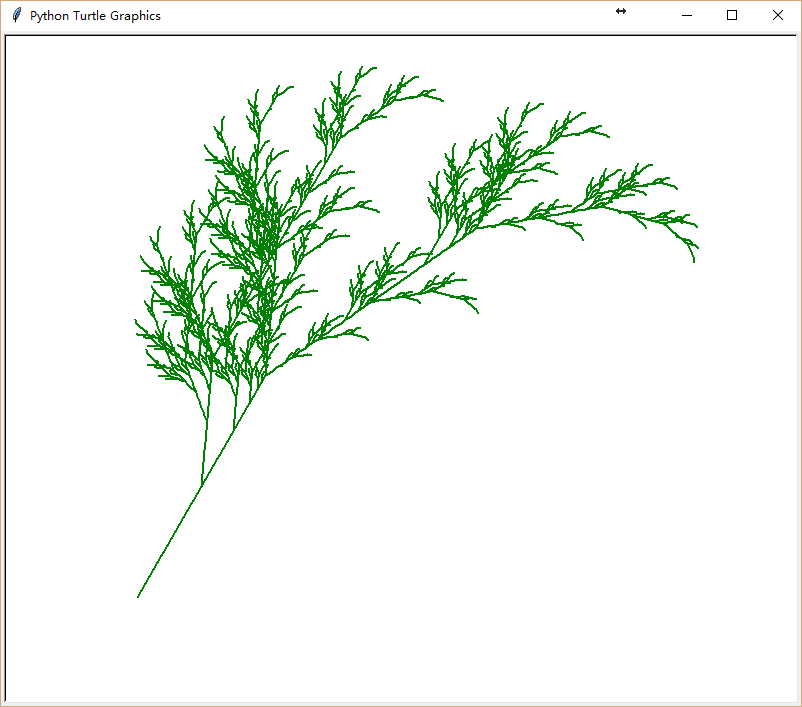
接下来让我们再做一个综合练习——基于“L系统”绘制一株“分形植物”：

"""使用L系统模拟的分形植物
"""
import turtle as tt


def generate(n, result="[X]"):
    """传入迭代次数和生成式返回结果序列
    """
    rules = {"X": "F-[[X]+X]+F[+FX]-X",
             "F": "FF"}
    for _ in range(n):
        for k, v in rules.items():
            result = result.replace(k, v)
    return result


def draw(cmds, size=2):
    """传入结果序列和线段长度绘制图形
    """
    stack = []
    for cmd in cmds:
        if cmd == "F":
            tt.forward(size)
        elif cmd == "-":
            tt.left(25)
        elif cmd == "+":
            tt.right(25)
        elif cmd == "X":
            pass
        elif cmd == "[":
            stack.append((tt.position(), tt.heading()))
        elif cmd == "]":
            position, heading = stack.pop()
            tt.penup()
            tt.setposition(position)
            tt.setheading(heading)
            tt.pendown()
        else:
            raise ValueError("Unknown Cmd: {}".format(ord(cmd)))
    tt.update()


def main():
    """绘图程序主函数
    """
    tt.TurtleScreen._RUNNING = True
    tt.hideturtle()
    tt.tracer(0)
    tt.color("green")
    tt.speed(0)
    tt.left(60)
    tt.pensize(2)
    tt.penup()
    tt.goto(-tt.window_width()/3, -tt.window_height()/3)
    tt.pendown()
    plant = generate(6)
    draw(plant)
    tt.exitonclick()


if __name__ == "__main__":
    main()

09_plant.png

以上程序使用一个字典来描述“L系统”文法的替换规则，因为只有两条规则，其实写两次replace方法就行，但用字典会更灵活——你可以继续改进生成函数增加一个规则参数，在调用时传入特定的规则字典，就能画出各种不同的分形图案了。

——编程原来是这样……

编程小提示：L系统

“L系统”是由匈牙利生物学家林登麦伊尔（Lindenmayer）于1968年提出的有关生长发展中的细胞交互作用的数学模型，目前被用来模拟各种生物体的形态，也能用于生成任何自相似的分形结构。例如以下文法描述了一株分形植物：

变量 : X F
常量 : + − [ ]
初始 : X
规则 : (X → F-[[X]+X]+F[+FX]-X), (F → FF)
角度 : 25°

X只用于迭代，F是画线段，+是右转，-是左转，方括号表示入栈和出栈。你可以用交互模式查看每次迭代的结果：

In [1]: from plant import generate

In [2]: generate(0)
Out[2]: '[X]'

In [3]: generate(1)
Out[3]: '[FF-[[X]+X]+FF[+FFX]-X]'

In [4]: generate(2)
Out[4]: '[FFFF-[[FF-[[X]+X]+FF[+FFX]-X]+FF-[[X]+X]+FF[+FFX]-X]+FFFF[+FFFFFF-[[X]+X]+FF[+FFX]-X]-FF-[[X]+X]+FF[+FFX]-X]'

迭代6次所生成的结果已长达31209个字符——简单规则蕴育出复杂结果，我们的世界就是因此而变得千姿百态……要了解L系统的详情可参看维基百科 https://en.wikipedia.org/wiki/L-system

下一篇：编程入门10：Python图形界面