细数目标检测中的损失函数
原文链接:https://www.yuque.com/yahei/hey-yahei/objects_detection#zoJwH
损失函数
目标检测中最经典的损失函数就是Faster RCNN所用的“softmax交叉熵分类损失 + SmoothL1回归损失”的形式,后来有很多改进的目标检测网络、方案也陆续提出了一些损失函数上的改进。
分类损失
参考:
- 《目标检测小tricks–样本不均衡处理 | 知乎, 燕小花》
- 《样本贡献不均:Focal Loss和 Gradient Harmonizing Mechanism | 知乎, BeyondTheData》
- 《Imbalance Problems in Object Detection: A Review (IEEE-PAMI2020)》
分类损失的改进主要是解决目标检测中样本不均衡的问题,通常是给难易样本设置一个自适应的权重损失。
Focal Loss
论文:《Focal Loss for Dense Object Detection (ICCV2017)》RetinaNet
作者设计了一个自适应加权的loss,为难样例设置更大的权重,从而提升训练效果。
首先考虑一个二分类的交叉熵(为方便起见,用二分类进行讨论,同理可推广至多分类情况),
C E ( p t ) = − l o g ( p t ) = { − l o g ( p ) , y = 1 − l o g ( 1 − p ) , y = − 1 CE(p_t) = -log(p_t) = \begin{cases} -log(p), & y=1 \\ -log(1-p), & y=-1 \end{cases} CE(pt)=−log(pt)={−log(p),−log(1−p),y=1y=−1
其中, y ∈ { − 1 , 1 } y \in \{-1, 1\} y∈{−1,1},而 p p p是预测为 y = 1 y=1 y=1的概率
加入一个人工设置的权重 α \alpha α,缓解样本不均衡的问题,
$$CE’(p_t) = - \alpha_t log(p_t) = \begin{cases}
- \alpha log§, & y=1 \
- (1-\alpha) log(1-p), & y=-1
\end{cases} < b r / > < b r / > 引 入 一 个 自 适 应 的 权 重 , 为 难 样 例 设 置 更 大 的 权 重 , < b r / >
引入一个自适应的权重,为难样例设置更大的权重,
<br/><br/>引入一个自适应的权重,为难样例设置更大的权重,<br/>FL(p_t) = - (1 - p_t)^\gamma \ log(p_t)$$
 - γ \gamma γ是人为设置的超参
- γ \gamma γ越大,难/易样例权重差异就越大
- 当 γ = 0 \gamma = 0 γ=0时,Focal Loss退化为Cross Entropy
- 在论文的实验中, γ = 2 \gamma = 2 γ=2时表现最佳
- 权重 ( 1 − p t ) γ (1-p_t)^\gamma (1−pt)γ会随着正确分类的置信度 p t p_t pt变化
- 当 p t p_t pt比较大时,正确分类的置信度高,属于易样例,权重就比较小
- 当 p t p_t pt比较小时,正确分类的置信度低,属于难样例,权重就比较大
实际操作中,Focal Loss可以结合人工设置的 α \alpha α一起使用,即
F L ( p t ) = − α t ( 1 − p t ) γ l o g ( p t ) FL(p_t) = - \alpha_t \ (1 - p_t)^\gamma \ log(p_t) FL(pt)=−αt (1−pt)γ log(pt)
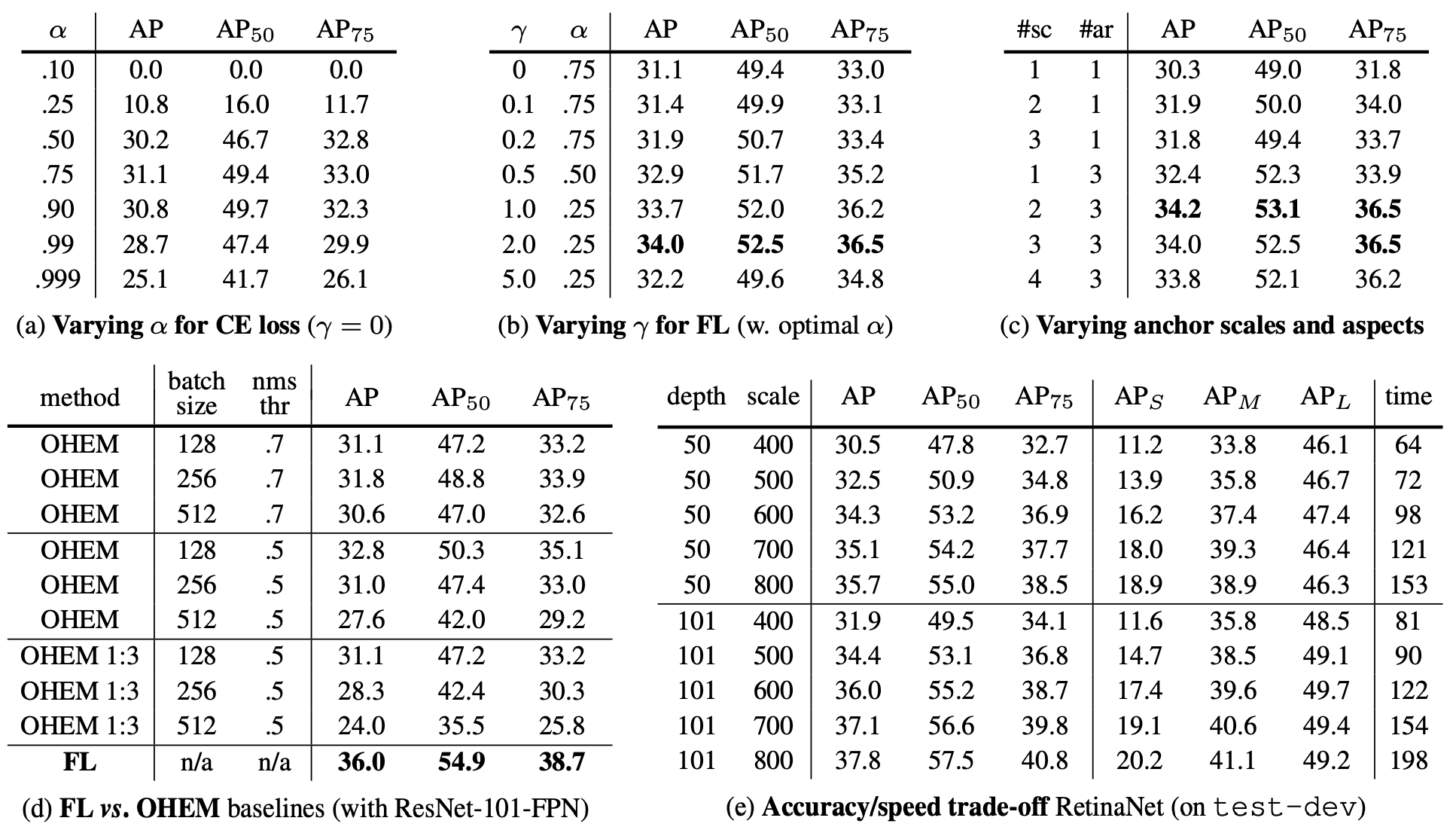
Focal Loss有两个超参 γ \gamma γ和 α \alpha α需要设置,之后一些新的分类损失则进一步简化了形式,提出一些不需要设置额外超参的loss。
Class-Balanced Loss
论文:《Class-Balanced Loss Based on Effective Number of Samples (CVPR2019)》 参考译文
论文提出用样本数量来调节为已有的损失函数加权,以此来缓解样本不均衡问题,应用在Focal Loss上则为
C B focal ( z , y ) = − 1 − β 1 − β n y ∑ i = 1 C ( 1 − p i t ) γ log ( p i t ) \mathrm{CB}_{\text {focal }}(\mathbf{z}, y)=-\frac{1-\beta}{1-\beta^{n_{y}}} \sum_{i=1}^{C}\left(1-p_{i}^{t}\right)^{\gamma} \log \left(p_{i}^{t}\right) CBfocal (z,y)=−1−βny1−βi=1∑C(1−pit)γlog(pit)
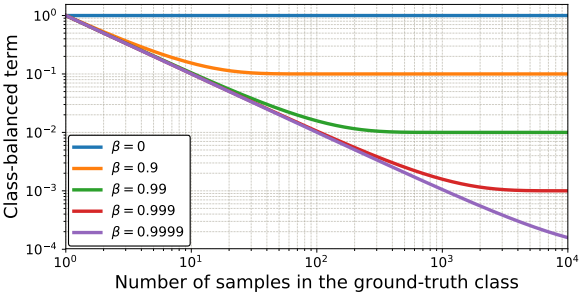
其中,
β ∈ ( 0 , 1 ) \beta \in (0, 1) β∈(0,1)是一个超参;
n y n_y ny是训练集上类别 y y y的样本数;
当 n y n_y ny越大, β n y \beta^{n_y} βny越小,权重 1 − β 1 − β n y \frac{1-\beta}{1-\beta^{n_y}} 1−βny1−β越小,也即样本数量越多,那么他对损失的贡献就越小
AP Loss
论文:《Towards Accurate One-Stage Object Detection With AP-Loss (CVPR2019)》
参考:《感知算法论文(九):Towards Accurate One-Stage Object Detection with AP-Loss | CSDN, 呆呆的猫》
Average Precision Loss(AP Loss)对每个预测框进行排序,用排序后的序号来设计loss,核心思想在于鼓励正样本预测框的得分在负样本得分序列中尽可能靠前。启发自AUC Loss,后者用AUC的排序序号来设计loss,直接对AUC进行优化,而目标检测通常以mAP为指标,因此作者指出直接对AP进行优化能有更好的效果。
Bounding Box的设置方式跟传统的设置方式有些不同。比如有 K K K个分类,
- 传统上是为每个Bounding Box预测一个分类 t i t_i ti( t i ∈ [ 0 , K ] t_i \in [0, K] ti∈[0,K],0表示背景)以及得分向量 ( s i 0 , s i 1 , . . . , s i K ) (s_i^0, s_i^1, ..., s_i^K) (si0,si1,...,siK)
- 论文则是把Bounding Box复制 K K K次,分别用于某一个分类 t i k ∈ { − 1 , 0 , 1 } t_{ik} \in \{-1, 0, 1\} tik∈{−1,0,1}(-1表示忽略,不纳入AP Loss的计算)的预测,以及得分 s i k s_{ik} sik
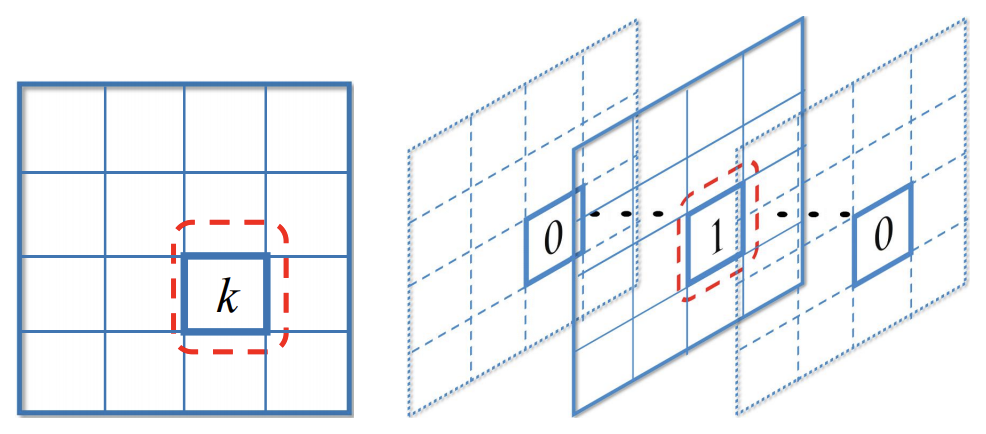
(左:一个label,属于分类k; 右:K个label,第k个为1)
AP Loss的具体设计(与GTBox的IoU超过阈值为正样本,否则为负样本):
- 所有预测框两两之间的得分差值
$$x_{i j}=-\left(s_{i}-s_{j}\right)\$$ - 计算每个预测框的归一化排序(在所有预测框中的排序)
$$L_{ij} = \begin{cases}
0, & s_i > s_j \
\frac{1}{1 + N_{i}}, & s_i \leq s_j
\end{cases}\ < b r / > 其 中 ,
其中, <br/>其中,N_{i} 是 得 分 大 于 等 于 是得分大于等于 是得分大于等于s_i 的 所 有 预 测 框 数 量 ( 包 括 正 负 样 本 ) ; < b r / > 显 然 , 的所有预测框数量(包括正负样本);
显然, 的所有预测框数量(包括正负样本);<br/>显然,L_i = \sum_{j \in P \cup N} L_{ij} 就 是 第 就是第 就是第i 个 预 测 框 在 所 有 预 测 框 中 的 排 序 序 号 , 而 个预测框在所有预测框中的排序序号,而 个预测框在所有预测框中的排序序号,而L_i^{(N)} = \sum_{j \in N} L_{ij} 就 是 第 就是第 就是第i 个 预 测 框 的 得 分 在 所 有 负 样 本 框 中 的 一 个 排 位 ( 归 一 化 的 序 号 , 序 号 越 小 则 得 分 个预测框的得分在所有负样本框中的一个排位(归一化的序号,序号越小则得分 个预测框的得分在所有负样本框中的一个排位(归一化的序号,序号越小则得分s_i 越 高 ) ; < b r / > 也 可 以 展 开 成 关 于 越高);
也可以展开成关于 越高);<br/>也可以展开成关于x_{ij} 的 数 学 描 述 , 的数学描述, 的数学描述,L_{i j}=\frac{H\left(x_{i j}\right)}{1+\sum_{k \in \mathcal{P} \cup \mathcal{N}, k \neq i} H\left(x_{i k}\right)}\ < b r / > 其 中 ,
其中, <br/>其中,H(\cdot) 为 阶 跃 函 数 , 为阶跃函数, 为阶跃函数,H(x)=\left{\begin{array}{ll}
0 & x<0 \
1 & x \geq 0
\end{array}\right.$$ - 计算AP Loss
$$\mathcal{L}{A P}=\frac{1}{|\mathcal{P}|} \sum{i \in \mathcal{P}} \sum_{j \in \mathcal{N}} L_{i j} \ < b r / > 其 中 ,
其中, <br/>其中,|\mathcal{P}| 是 正 样 本 预 测 框 的 数 量 ; 也 可 以 写 成 , < b r / > 是正样本预测框的数量;也可以写成,
是正样本预测框的数量;也可以写成,<br/>\mathcal{L}{A P}=\frac{1}{|\mathcal{P}|} \sum{i, j} L_{i j} \cdot y_{i j} = \frac{1}{|\mathcal{P}|} \sum_{i, j} L_{i j}
\cdot \mathbf{1}{t{i}=1, t_{j}=0}\$$ - 显然 L A P \mathcal{L}_{A P} LAP是不可导,所以需要定义近似的更新规则$$\Delta x_{i j}=L_{i j}^{}-L_{i j} \ < b r / >
<br/>L^{ij} 是 真 实 值 。 < b r / > 当 是真实值。
当 是真实值。<br/>当y{ij}=1 时 , 时, 时,L^*{ij}=0 , 因 为 我 们 目 标 是 让 正 样 本 预 测 框 的 得 分 比 所 有 负 样 本 预 测 框 都 高 ; < b r / > 当 ,因为我们目标是让正样本预测框的得分比所有负样本预测框都高;
当 ,因为我们目标是让正样本预测框的得分比所有负样本预测框都高;<br/>当y{ij} = 0 时 , 时, 时,\Delta x_{ij} = 0 , 因 为 它 不 对 A P L o s s 产 生 贡 献 ; < b r / > 因 此 , 可 以 简 化 成 < b r / > ,因为它不对AP Loss产生贡献;
因此,可以简化成
,因为它不对APLoss产生贡献;<br/>因此,可以简化成<br/>\Delta x_{ij} = - L_{ij} \cdot y_{ij} = - L_{i j}
\cdot \mathbf{1}{t{i}=1, t_{j}=0}\$$
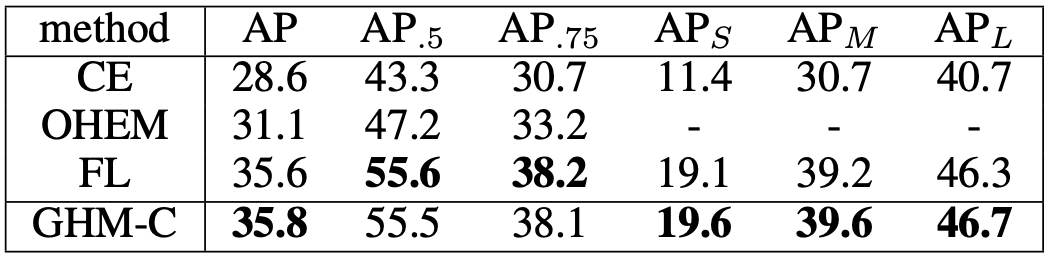
相比于Focal Loss有比较明显的提升,而且不需要调整任何超参:
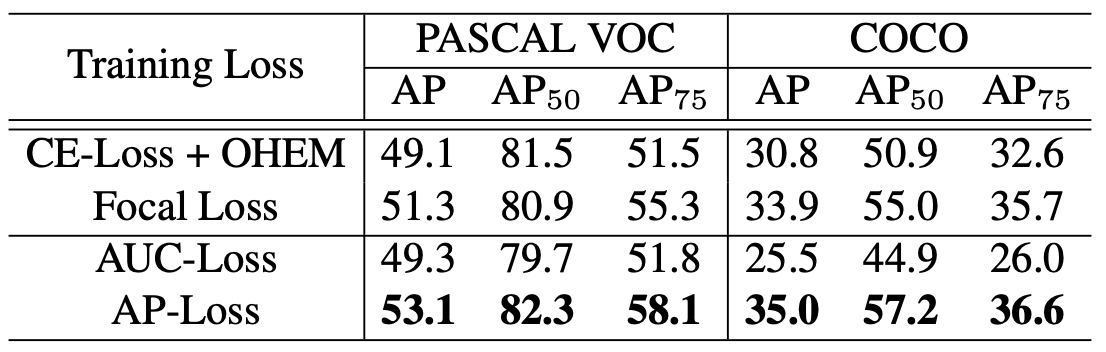
(在RetinaNet上使用不同分类损失的实验结果)
GHM-C Loss
论文:《Gradient Harmonized Single-stage Detector (AAAI2019)》GHM-C和GHM-R
Gradient Harmonized Mechanism(GHM)通过利用计算损失前的特征的梯度信息,对原损失进行规范化操作。包括针对分类损失改进的GHM-C和针对回归损失改进的GHM-R。该损失只有一个超参。
考虑某一分类的交叉熵
L C E ( p , p ∗ ) = { − log ( p ) if p ∗ = 1 − log ( 1 − p ) if p ∗ = 0 L_{C E}\left(p, p^{*}\right)=\left\{\begin{array}{ll} -\log (p) & \text { if } p^{*}=1 \\ -\log (1-p) & \text { if } p^{*}=0 \end{array}\right. LCE(p,p∗)={−log(p)−log(1−p) if p∗=1 if p∗=0
其中 p = s i g m o i d ( x ) p = sigmoid(x) p=sigmoid(x),那么(注意这里的对数是自然对数),
∂ L C E ∂ x = ∂ L C E ∂ p ∂ p ∂ x = { p − 1 if p ∗ = 1 p if p ∗ = 0 = p − p ∗ \begin{aligned} \frac{\partial L_{C E}}{\partial x}&= \frac{\partial L_{C E}}{\partial p}\frac{\partial p}{\partial x} \\ &=\left\{\begin{array}{ll} p-1 & \text { if } p^{*}=1 \\ p & \text { if } p^{*}=0 \end{array}\right. \\ &= p - p^* \end{aligned} ∂x∂LCE=∂p∂LCE∂x∂p={p−1p if p∗=1 if p∗=0=p−p∗
记梯度的绝对值为 g = ∣ ∂ L C E ∂ x ∣ = ∣ p − p ∗ ∣ g = |\frac{\partial L_{C E}}{\partial x}| = |p - p^*| g=∣∂x∂LCE∣=∣p−p∗∣;
显然, g ∈ [ 0 , 1 ] g \in [0, 1] g∈[0,1], g g g越大,那么这个样例就越hard;
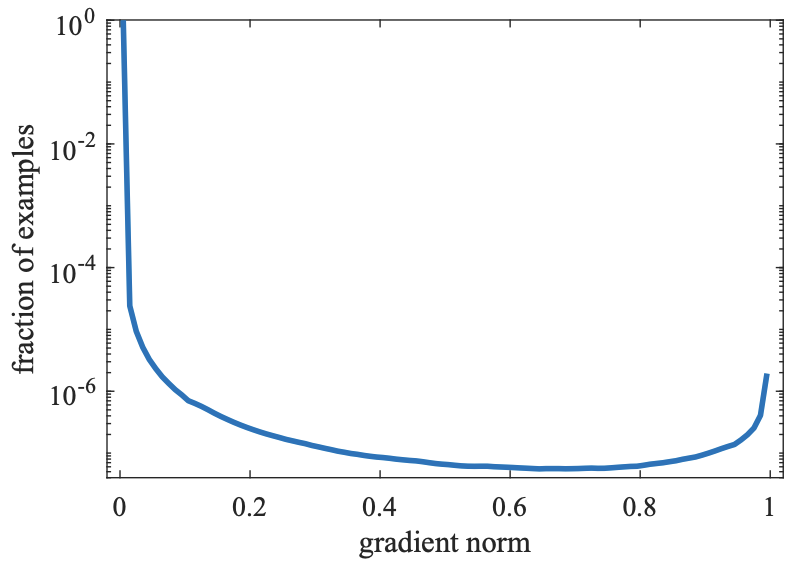
如上图所示,对于一个收敛的检测网络,
- 有巨量的easy负样例(以至于需要用对数坐标轴来绘制这张图),它们却对全局梯度产生很大的贡献
- 同时还是有不少的very hard样例,这说明还有很多这种hard样例并没有学好
- 如果能够让网络聚焦在这些very hard样例的学习上,那么网络会有明显的提升
接下来定义第 i i i个样例上的梯度密度,
G D ( g i ) = 1 l ϵ ( g i ) ∑ k = 1 N δ ϵ ( g k , g i ) G D(g_i)=\frac{1}{l_{\epsilon}(g_i)} \sum_{k=1}^{N} \delta_{\epsilon}\left(g_{k}, g_i\right) GD(gi)=lϵ(gi)1k=1∑Nδϵ(gk,gi)
其中, N N N为一个batch的样例数, ϵ \epsilon ϵ是一个宽度,而
δ ϵ ( x , y ) = { 1 if y − ϵ 2 ≤ x < y + ϵ 2 0 otherwise \delta_{\epsilon}(x, y)=\left\{\begin{array}{ll} 1 & \text { if } y-\frac{\epsilon}{2}\leq x
l ϵ ( g i ) = min ( g i + ϵ 2 , 1 ) − max ( g i − ϵ 2 , 0 ) l_{\epsilon}(g_i)=\min \left(g_i+\frac{\epsilon}{2}, 1\right)-\max \left(g_i-\frac{\epsilon}{2}, 0\right) lϵ(gi)=min(gi+2ϵ,1)−max(gi−2ϵ,0)
直观点理解,
∑ k = 1 N δ ϵ ( g k , g i ) \sum_{k=1}^{N} \delta_{\epsilon}\left(g_{k}, g_i\right) k=1∑Nδϵ(gk,gi)表示在所有样例中,梯度绝对值在 g i g_i gi附近( ± ϵ 2 \pm \frac{\epsilon}{2} ±2ϵ范围内)的样例数量;
1 l ϵ ( g i ) \frac{1}{l_\epsilon(g_i)} lϵ(gi)1按照区间宽度 ϵ \epsilon ϵ对数量 ∑ k = 1 N δ ϵ ( g k , g i ) \sum_{k=1}^{N} \delta_{\epsilon}\left(g_{k}, g_i\right) k=1∑Nδϵ(gk,gi)进行规范化处理,将 l ϵ ( g i ) l_\epsilon(g_i) lϵ(gi)具体展开来为
l ϵ ( g i ) = { g i + ϵ 2 , 0 ≤ g i ≤ ϵ 2 ϵ , ϵ 2 < g i ≤ 1 − ϵ 2 1 + ϵ 2 − g i , 1 − ϵ 2 < g i ≤ 1 l_\epsilon(g_i) = \begin{cases} g_i + \frac{\epsilon}{2}, & 0 \leq g_i \leq \frac{\epsilon}{2} \\ \epsilon, & \frac{\epsilon}{2} < g_i \leq 1 - \frac{\epsilon}{2} \\ 1 + \frac{\epsilon}{2} - g_i, & 1 - \frac{\epsilon}{2} < g_i \leq 1 \end{cases} lϵ(gi)=⎩⎪⎨⎪⎧gi+2ϵ,ϵ,1+2ϵ−gi,0≤gi≤2ϵ2ϵ<gi≤1−2ϵ1−2ϵ<gi≤1
显然, 1 l ϵ ( g i ) \frac{1}{l_\epsilon(g_i)} lϵ(gi)1对小梯度和大梯度对应的梯度密度都做了一些抑制处理。
进一步用归一化梯度密度来定义一个梯度密度协变量(gradient density harmonizing parameter),
β i = 1 G D ( g i ) / N = N G D ( g i ) \beta_{i}=\frac{1}{G D\left(g_{i}\right) / N} = \frac{N}{G D\left(g_{i}\right)} βi=GD(gi)/N1=GD(gi)N
最后用 β ^ i \hat{\beta}_i β^i为不同样例的损失进行加权以平衡难易样例的权重,
L G H M − C = 1 N ∑ i = 1 N β i L C E ( p i , p i ∗ ) = ∑ i = 1 N L C E ( p i , p i ∗ ) G D ( g i ) \begin{aligned} L_{G H M-C}&=\frac{1}{N} \sum_{i=1}^{N} \beta_{i} L_{C E}\left(p_{i}, p_{i}^{*}\right) \\ &= \sum_{i=1}^{N} \frac{L_{C E}\left(p_{i}, p_{i}^{*}\right)}{GD(g_i)} \end{aligned} LGHM−C=N1i=1∑NβiLCE(pi,pi∗)=i=1∑NGD(gi)LCE(pi,pi∗)
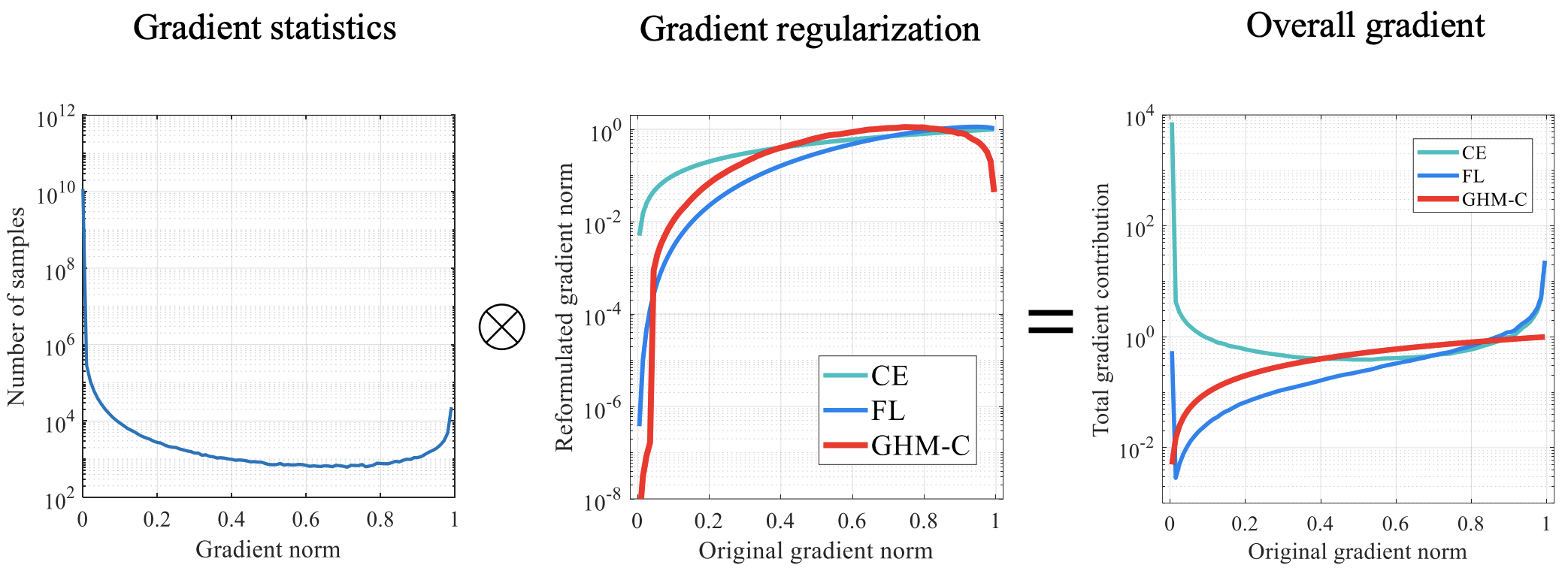
如上图所示,CE、FL、GHM-C都可以看作是对梯度分布正则化的过程,将梯度范数调整到一个相对平缓的范围内。FL仅仅抑制了小梯度的样例数量(主要是easy负样例),而GHM-C同时抑制了大梯度的样例数量(very hard样例)。
GHM-C依赖于mini-batch的统计结果,跟BN一样,要求batch-size不能太小,否则统计量不准确将导致训练过程不稳定。
实验结果:似乎比Focal Loss稍微好一点点,但不明显
为了降低梯度密度的计算复杂度,提出了一种近似算法:
- 找到梯度 ( g 1 , g 2 , . . . , g N ) (g_1, g_2, ..., g_N) (g1,g2,...,gN)的最大值 g m a x g_{max} gmax最小值 g m i n g_{min} gmin;
- 将区间 [ g m i n , g m a x ] [g_{min}, g_{max}] [gmin,gmax]等分为 M M M个子区间(Unit Region),那么有 M = 1 ϵ M = \frac{1}{\epsilon} M=ϵ1;
- 记 R j R_j Rj为第 j j j个区间 [ ( j − 1 ) ϵ , j ϵ ) [(j-1)\epsilon, j\epsilon) [(j−1)ϵ,jϵ)中包含的样例数量,那么可以近似求得
G D ^ ( g i ) = R i ϵ = R i M β ^ i = N G D ^ ( g i ) \hat{GD}(g_i) = \frac{R_i}{\epsilon} = R_i M \\ \hat{\beta}_i = \frac{N}{\hat{GD}(g_i)} GD^(gi)=ϵRi=RiMβ^i=GD^(gi)N - 只要 M M M足够大,就能比较好近似原始设计(如论文实验取 M = 30 M=30 M=30能得到最佳效果)
- 考虑到算法涉及mini-batch内的统计量,有可能出现某个mini-batch里出现一些极端值导致训练不稳定。为了稳定数值,可以采用指数平滑平均EMA进行处理
S i ( t ) = α S i ( t − 1 ) + ( 1 − α ) R i ( t ) G D ^ ( g i ) = S i ϵ = S i M S_i^{(t)} = \alpha S_i^{(t-1)} + (1-\alpha) R_i^{(t)} \\ \hat{GD}(g_i) = \frac{S_i}{\epsilon} = S_i M Si(t)=αSi(t−1)+(1−α)Ri(t)GD^(gi)=ϵSi=SiM - 实验比较(原始设计的训练速度非常慢)

(GHM-C Standard和GHM-C RU分别表示原始设计和近似设计)
回归损失
参考:
- 《目标检测位置回归损失函数整理 | 知乎, 江小鱼》
- 《IoU、GIoU、DIoU损失函数的那点事儿 | 知乎, Error》
原始的回归损失是直接利用L1、L2或SmoothL1对坐标值/尺度进行数值回归,GHM-R是GHM在提出GHM-C分类损失的同时,采取类似的处理的一种改进思路;后来出现了直接用IoU来设计回归损失,再后来回归损失的改进都是对框回归好坏的指标改进,先后出现了GIoU、DIoU等对IoU的改进方案,从而衍生出对应的回归损失。
GHM-R Loss
论文:《Gradient Harmonized Single-stage Detector (AAAI2019)》GHM-C和GHM-R
沿用GHM-C Loss的思路设计新的回归损失函数,直觉告诉我们可以这样做:
$$L_{G H M-R}=\frac{1}{N} \sum_{i=1}^{N} \beta_{i} L_{SL}\left(t_i - t_i^\right) \ < b r / > 其 中 , < b r / >
其中,
<br/>其中,<br/>L_{SL} 为 S m o o t h L 1 损 失 函 数 ; < b r / > 而 关 于 为SmoothL1损失函数;
而关于 为SmoothL1损失函数;<br/>而关于t_i 的 含 义 可 以 参 见 F a s t e r R C N N 的 预 测 框 修 正 一 节 , 为 方 便 进 一 步 解 释 , 记 的含义可以参见Faster RCNN的预测框修正一节,为方便进一步解释,记 的含义可以参见FasterRCNN的预测框修正一节,为方便进一步解释,记d_i = t_i - t_i^$$。
接下来考虑 β i \beta_i βi的合理性,
β i = N G D ( ∂ L S L ∂ d ) \beta_i = \frac{N}{GD(\frac{\partial L_{SL}}{\partial d})} βi=GD(∂d∂LSL)N
而
L S L ( d i ) = { d i 2 2 δ if ∣ d i ∣ < = δ ∣ d i ∣ − δ 2 otherwise L_{SL}(d_i) = \left\{\begin{array}{ll} \frac{d_i^{2}}{2 \delta} & \text { if }|d_i|<=\delta \\ |d_i|-\frac{\delta}{2} & \text { otherwise } \end{array}\right. LSL(di)={2δdi2∣di∣−2δ if ∣di∣<=δ otherwise
其中, δ \delta δ是认为设置的超参。
那么
∂ L S L ∂ d i = { d i δ if ∣ d i ∣ < = δ sign ( d i ) otherwise \frac{\partial L_{SL}}{\partial d_i} = \left\{\begin{array}{ll} \frac{d_i}{\delta} & \text { if }|d_i|<=\delta \\ \operatorname{sign}(d_i) & \text { otherwise } \end{array}\right. ∂di∂LSL={δdisign(di) if ∣di∣<=δ otherwise
由于GHM-R依赖梯度信息来计算Loss,所以要求不同样例的梯度能有一定的区分度。
但这里的 s i g n ( d i ) ∈ { − 1 , + 1 } sign(d_i) \in \{-1, +1\} sign(di)∈{−1,+1},于是作者设计了另一种与SmoothL1有类似效果的损失:
L A S L = d i 2 + μ 2 − μ ∂ L A S L ∂ d i = d i d i 2 + μ 2 L_{ASL} = \sqrt{d_i^{2}+\mu^{2}}-\mu \\ \frac{\partial L_{ASL}}{\partial d_i}=\frac{d_i}{\sqrt{d_i^{2}+\mu^{2}}} LASL=di2+μ2−μ∂di∂LASL=di2+μ2di
那么,记 g r i = ∂ L A S L ∂ d i gr_i = \frac{\partial L_{ASL}}{\partial d_i} gri=∂di∂LASL,则
L G H M − R = 1 N ∑ i = 1 N β i L A S L ( t i − t i ∗ ) = ∑ i = 1 N L A S L ( t i − t i ∗ ) G D ( g r i ) \begin{aligned} L_{G H M-R}&=\frac{1}{N} \sum_{i=1}^{N} \beta_{i} L_{ASL}\left(t_i - t_i^*\right) \\ &= \sum_{i=1}^{N} \frac{L_{ASL}\left(t_i - t_i^*\right)}{GD(gr_i)} \end{aligned} LGHM−R=N1i=1∑NβiLASL(ti−ti∗)=i=1∑NGD(gri)LASL(ti−ti∗)
实验结果:SL和ASL效果相近,GHM-R则有少量提升

IoU Loss
论文:《UnitBox: An Advanced Object Detection Network (ACM-MM2016)》
早前的L1、L2、SmoothL1损失都只把每个(规范化的)坐标值/尺度当作独立的变量训练,没有考虑它们内在的联系,因此提出用IoU的交叉熵来设计损失。
I o U L o s s = − p ⋅ l o g ( I o U ) − ( 1 − p ) l o g ( 1 − I o U ) = − l o g ( I o U ) \begin{aligned} IoU\ Loss &= - p \cdot log(IoU) - (1-p)log(1-IoU) \\ &= -log(IoU) \end{aligned} IoU Loss=−p⋅log(IoU)−(1−p)log(1−IoU)=−log(IoU)
IoU Loss在设计损失时为(规范化的)坐标值/尺度建立了联系,可以直接反映预测框的检测效果,同时IoU对尺度也不敏感。
但是,GIoU的论文也指出了IoU的一些缺点,
- 对于不与真实框重叠的预测框, I o U = 0 IoU=0 IoU=0,此时损失为零,对网络的学习过程没有贡献
- 在某些情况下(尤其是允许预测框旋转的情况下),IoU指标似乎不够合理。如下图所示,三组的IoU是相等的,但直观上判断回归的效果是:左 > 中 > 右
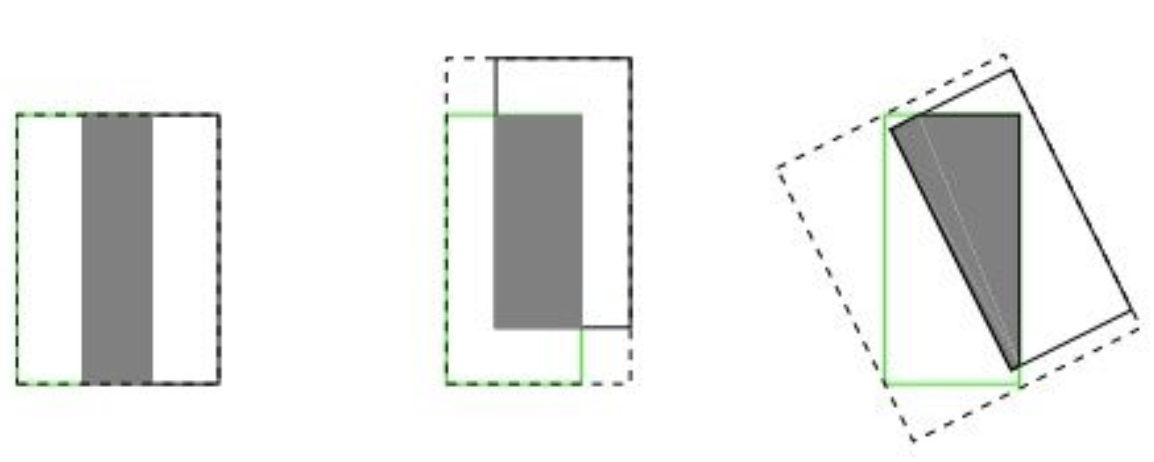
GIoU Loss
论文:《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression (CVPR2019)》
G I o U = I o U − ∣ A c − U ∣ ∣ A c ∣ G I o U=I o U-\frac{\left|A_{c}-U\right|}{\left|A_{c}\right|} GIoU=IoU−∣Ac∣∣Ac−U∣
G I o U L o s s = 1 − G I o U GIoU\ Loss = 1-GIoU GIoU Loss=1−GIoU
- 其中, A c A_c Ac是两个框之间的最小闭包框面积(也即能同时包含两个框的最小框面积);
最小闭包框面积的计算过程与IoU类似,
{ x ^ l t c = m i n ( x l t , x l t ′ ) y ^ l t c = m i n ( y l t , y l t ′ ) , { x ^ r b c = m a x ( x r b , x r b ′ ) y ^ r b c = m a x ( y r b , y r b ′ ) A c = ( x ^ r b c − x ^ l t c ) ( y ^ r b c − y ^ l t c ) \begin{cases} \hat{x}_{lt}^c = min(x_{lt}, x'_{lt}) \\ \hat{y}_{lt}^c = min(y_{lt}, y'_{lt}) \end{cases} , \begin{cases} \hat{x}_{rb}^c = max(x_{rb}, x'_{rb}) \\ \hat{y}_{rb}^c = max(y_{rb}, y'_{rb}) \end{cases} \\ A_c = (\hat{x}_{rb}^c - \hat{x}_{lt}^c)(\hat{y}_{rb}^c - \hat{y}_{lt}^c) {x^ltc=min(xlt,xlt′)y^ltc=min(ylt,ylt′),{x^rbc=max(xrb,xrb′)y^rbc=max(yrb,yrb′)Ac=(x^rbc−x^ltc)(y^rbc−y^ltc)
( x ^ l t c , y ^ l t c , x ^ r b c , y ^ r b c ) (\hat{x}_{lt}^c,\hat{y}_{lt}^c,\hat{x}_{rb}^c,\hat{y}_{rb}^c) (x^ltc,y^ltc,x^rbc,y^rbc)与 ( x ^ l t , y ^ l t , x ^ r b , y ^ r b ) (\hat{x}_{lt},\hat{y}_{lt},\hat{x}_{rb},\hat{y}_{rb}) (x^lt,y^lt,x^rb,y^rb)的差别无非是把 m i n ( ⋅ ) min(\cdot) min(⋅)和 m a x ( ⋅ ) max(\cdot) max(⋅)翻了过来 - G I o U ∈ [ − 1 , 1 ] GIoU \in [-1, 1] GIoU∈[−1,1]
- 当 G I o U < 0 GIoU < 0 GIoU<0时,表明两个框不重叠,且 G I o U GIoU GIoU越小,两框的距离越远, G I o U = − 1 GIoU=-1 GIoU=−1时表明相距无穷远
- 当 G I o U > 0 GIoU > 0 GIoU>0时,表明两个框重叠,且 G I o U GIoU GIoU越大,两框的重合程度越好, G I o U = 1 GIoU=1 GIoU=1表明完全重合
- 解决了 I o U IoU IoU无法度量距离的问题
- G I o U GIoU GIoU依旧对具体的坐标值/尺度不敏感
- 不足之处在于,
- G I o U GIoU GIoU在考虑不重叠的情况时,只度量了距离却忽视了框的尺度
- 当两框恰好处于水平或垂直方向是, G I o U GIoU GIoU有可能几乎退化成 I o U IoU IoU
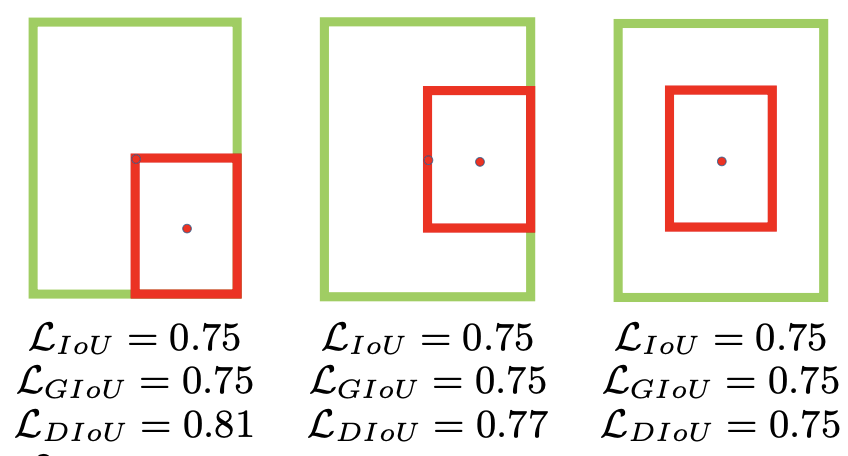
(它们的GIoU Loss相同,但显然第三种情况回归地更好)
DIoU Loss & CIoU Loss
论文:《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression (AAAI2020)》
D I o U = I o U − ρ 2 ( b , b g t ) c 2 D I o U=I o U-\frac{\rho^{2}\left(b, b^{g t}\right)}{c^{2}} DIoU=IoU−c2ρ2(b,bgt)
D I o U L o s s = 1 − D I o U DIoU\ Loss = 1 - DIoU DIoU Loss=1−DIoU
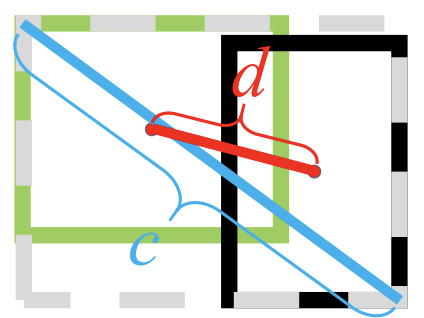
- 其中,
- b b b和 b g t b^{gt} bgt分别是预测框和真实框的中心点, d = ρ ( b , b g t ) d = \rho (b, b^{gt}) d=ρ(b,bgt)度量了两点之间的欧式距离;
- c c c是预测框和真实框的最小闭包框的对角线距离
- DIoU跟GIoU一样,能在两框不重叠时为训练提供方向
- DIoU在两框不重叠时既考虑了距离,也考虑了尺度
- 在两框处于水平或垂直方向上时,DIoU依旧能为训练网络做出不错的贡献
- DIoU直接最小化两框的距离,拥有更加平滑的损失曲面,因此收敛比GIoU更快
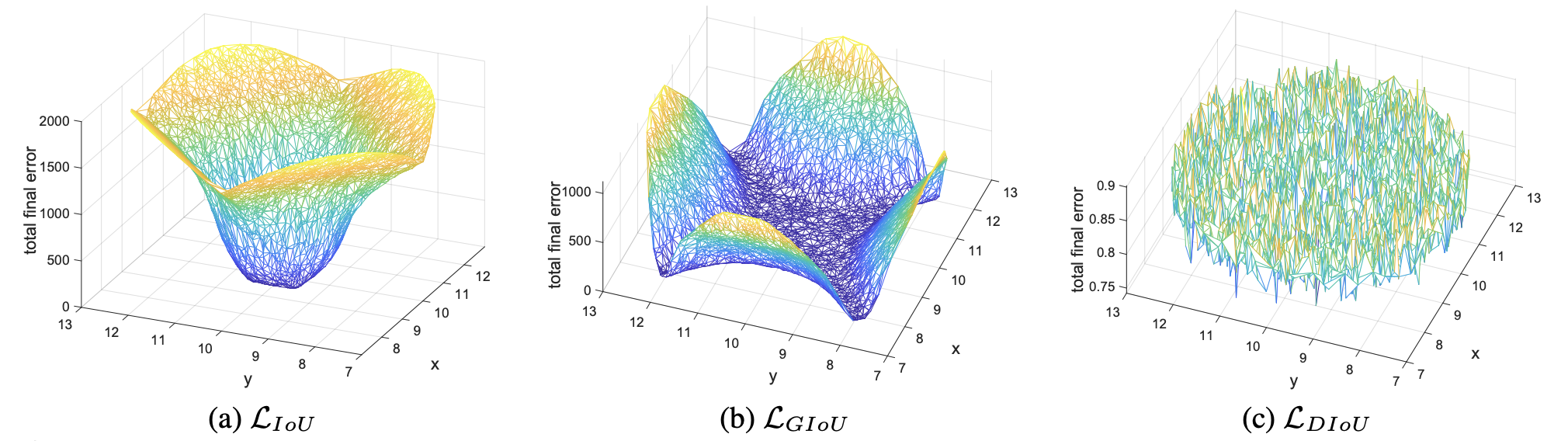
在DIoU Loss的基础上,论文继续引入长宽比的惩罚得到CIoU Loss:
C I o U L o s s = 1 − I o U + ρ 2 ( c , c g t ) d 2 + α v CIoU\ Loss =1 - I o U + \frac{\rho^{2}\left(c, c^{g t}\right)}{d^{2}} + \alpha v CIoU Loss=1−IoU+d2ρ2(c,cgt)+αv
其中,
α = v ( 1 − I o U ) + v v = 4 π 2 ( arctan w g t h g t − arctan w h ) 2 \begin{array}{c} \alpha=\frac{v}{(1-I o U)+v} \\ v=\frac{4}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right)^{2} \end{array} α=(1−IoU)+vvv=π24(arctanhgtwgt−arctanhw)2
v ∈ [ 0 , 1 ] v \in [0, 1] v∈[0,1]度量了两框的长宽比差异,完全相等时 v = 0 v=0 v=0;
α \alpha α是一个自适应的调节权重,目的是为了突出 I o U IoU IoU的回归,当 I o U IoU IoU比较小甚至 I o U = 0 IoU=0 IoU=0时,应当优先学习如何回归出能够重叠、重叠的比较好的预测框,而不是学习如何调整长宽比。
Yolo-v3在VOC2007上的实验结果:
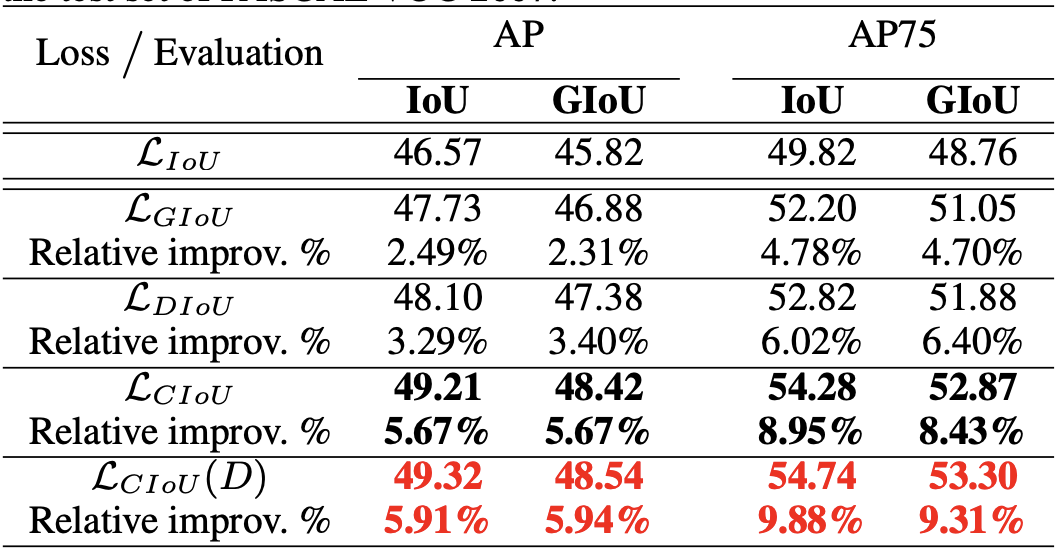
( ( D ) (D) (D)表示用DIoU来做NMS)