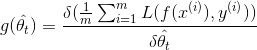深度学习最全梯度下降优化算法

前言

什么是梯度？方向导数是一个值而梯度是一个向量。方向导数是函数在各个方向的斜率，而梯度是斜率最大的方向，梯度的值是方向导数最大的值。

            当 Θ = 0 时，e 与梯度方向相同时，方向导数最大，函数增加最快

           当 Θ = pi 时，e 与梯度方向相反时，方向导数最小，函数减少最快

           当 Θ = pi/2 时，e 与梯度方向垂直时，方向导数为0， 函数变化率为零

反向传播通过梯度下降的方式来更新参数，以使得loss最小。公式如下：

                                               

代表学习率，作为参数控制梯度下降的步长。

1.SGD

随机梯度下降（Stochastic Gradient Descent, SGD）每次从训练样本中随机抽取一个样本计算loss和梯度并对参数进行更新；但这种优化算法比较弱，容易走偏，有时可用于在线学习（Online Learning）系统，可使系统快速学到新变化。

批量梯度下降（Batch Gradient Descent,BGD）算法每次使用整个训练集合计算梯度，这样计算的梯度比较稳定，相比随机梯度下降不那么容易震荡；单非常慢且无法放到内存中计算，更无法应用于在线学习系统。

介于随机梯度下降和批量梯度下降之间的是小批量梯度下降（Mini-Batch Gradient Descent)，即每次随机抽取m个样本，以它们的梯度均值作为梯度的近似估计。它可以降低参数更新时的方差，收敛更稳定，另一方面可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算。

在深度学习中常说的随机梯度下降通常是指小批量梯度下降。所以本博客中的SGD没有特别指出，都为小批量梯度下降。随机梯度下降的具体训练步骤如下所示，其中表示第i个样本的预测值，表示第i个样本的损失函数， 为m条数据的平均损失。

---

参数：学习率

初始化：

 while 停止条件未满足do

              从训练数据中抽取m条数据{}及对应的标签{}

              计算梯度：

              更新参数：

end while

---

为了使随机梯度下降获得较好的性能，学习率需要取值合理并根据训练过程动态调整。如果学习率过大，模型就会收敛过快，最终离最优值较远；如果学习率过小，迭代次数就会很多，导致模型长时间不能收敛。

2.Momentum

动量（Momentum）是来自物理力学中的一个概念，是力的时间积累效应的度量。动量的方法在随机梯度下降的基础上，加上了上一步的梯度：

其中是动量参数且。动量的优化方法也可以写为如下形式：

区别在于学习率的位置。如果对公式进行展开，不难发现两者是完全等价的。

相比随机梯度下降，动量会使相同方向的梯度不断累加，而不同方向的梯度则相互抵消，因而可以在一定程度上克服Z字形的震荡，更快到达最优点。具体算法细节如下所示：

---

参数：学习率，动量

初始化：

 while 停止条件未满足do

从训练数据中抽取m条数据{}及对应的标签{}

              计算梯度：

              更新参数：

                 

                

end while

---

3.NAG

Nesterov加速梯度（Nesterov Accelerated Gradient, NAG）与动量类似，也是考虑最近的梯度情况，但是NAG相对超前一点，它先使用动量计算参数下一个位置的近似值,然后再近似位置上计算梯度：

NAG与动量法的具体区别如图所示。从图中可以看出，NAG算法会计算本轮迭代时动量到达位置的梯度，可以说它计算的是“未来”的梯度。如果未来的梯度存在一定的规律，那么这些梯度就会有更好的利用价值。如果采用这种计算方式，梯度计算采用的是点A，前向计算采用的是原始的点O，这种不统一带来了额外的计算开销。

当然，在实际计算过程中，比如casse，为了前向、后向计算统一，引入了以下变量：

                   

                   

将上面两个公式代入，就可以得到：

                   

                  

将上面第一个公式代入第二个公式，就可以得到：

                   

整理得到：

                

这样梯度计算和前向计算不一致的问题就得到了解决。

NAG对应的算法如下所示：

---

参数：学习率，动量衰减率

初始化：

 while 停止条件未满足do

              从训练数据中抽取m条数据{}及对应的标签{}

              计算梯度：

              更新参数：

                              

                              

end while

---

 4.Adagrad

Adagrad是一种自适应的梯度下降算法，能够针对参数更新的频率来调整它们的跟新幅度，对于更新频繁且更新量大的参数，适当减小它们的步长；对于更新不频繁的参数，适当增加它们的步长。这种方法的思想很适合一些数据分布不均匀的任务。

它的具体更新方法是在之前梯度下降的基础上增加一个梯度的积累项作为分母，之前梯度下降法的参数更新公式为：

                      

而Adagrad变成：

                     

其中表示两个向量元素级的乘法，就是Adagrad增加的内容。它是所有轮迭代的梯度平方和：

                    

对于经常更新的参数，项的数值会比较大，因而它的参数更新量会得到控制；对于不常更新的参数，由于项的数值比较小，它的参数更新量会变大。完整的算法如下所示：

---

参数：学习率，微小量，梯度积累量G

初始化：

 while 停止条件未满足do

              从训练数据中抽取m条数据{}及对应的标签{}

              计算梯度：

              更新梯度积累量：

              更新参数：  

end while

---

5.RMSProp

RMSProp利用滑动平均的方法来解决Adagrad算法中的问题。它的思路是让梯度积累值G不要一直大，而是按照一定的比率衰减，这样其含义就不再是梯度的积累项了，而是梯度的平均值：

                                   

                                    

因为此时的G更像是梯度的平均值甚至期望值，因此在很多文献中会将G写成，具体算法如下所示：

---

参数：学习率，微小量，梯度积累量G，梯度积累量衰减率

初始化：

 while 停止条件未满足do

              从训练数据中抽取m条数据{}及对应的标签{}

              计算梯度：

              更新梯度积累量：

              更新参数：  

end while

---

6.Adadelta

Adadelta算法的思想和RMSProp算法比较接近，不过Adadelta考虑了一些更新量“单位”的问题。对比Adagrad算法和梯度下降法的更新公式，可以得到如下表所示的对比结果。

方法	更新
梯度下降
Adagrad

可以看出Adagrad算法和梯度下降法相比多出来一个项目，这样更新量的“单位”就和之前不同了。为了让“单位”匹配，Adadelta选择在分子上再增加一个项目，于是方法的概念公式变成：

                                     

其中RMS表示Root Mean Square，也就是“均方根”的意思。分母中的展开与RMSProp相同：

                            

分子部分也采用类似的方法，展开后得到：

                          

                                         

                                        

最终的算法如下所示：

---

参数：学习率，微小量，梯度积累量G，衰减率

初始化：

 while 停止条件未满足do

              从训练数据中抽取m条数据{}及对应的标签{}

              计算梯度：

              更新梯度积累量：

              计算参数更新量：  

  更新参数相关积累量：

  更新参数：

end while

---

7.Adam

Adam算法全称为Adaptive Moment Estimation,这种方法结合了上面提到的两类算法：基于动量的算法和基于自适应的算法。基于动量的算法有动量法和NAG法，这两种方法都基于历史的梯度信息进行参数更新。Adam算法记录了梯度的一阶矩（梯度的期望值）和二阶矩（梯度平方的期望值）：

                           

为了确保两个梯度积累量能够良好地估计梯度的一阶矩和二阶矩，两个积累量还需要乘以一个偏置纠正的系数：

                               

然后再使用两个积累量进行参数更新：

               

完整的算法流程如下所示：

---

参数：学习率，微小量，一阶矩，二阶矩，衰减率、

初始化：

 while 停止条件未满足do

              从训练数据中抽取m条数据{}及对应的标签{}

              计算梯度：

              更新一阶矩：

              更新二阶矩：

              纠正一阶矩：

             纠正二阶矩：

              计算参数更新量： 

  更新参数：

end while

---

8.AdaMax

AdaMax算法主要针对Adam算法进行了修改，而修改的位置在二阶矩这里。AdaMax将二阶矩修改为无穷矩，这样在数值上更加稳定：

                     

将替换成后，最终的更新变为：

                   

此时的无穷矩估计不再是有偏的，因此也不需要再做纠正。最终的算法如下所示：

---

参数：学习率，微小量，一阶矩，二阶矩，衰减率、

初始化：

 while 停止条件未满足do

              从训练数据中抽取m条数据{}及对应的标签{}

              计算梯度：

              更新一阶矩：

              更新无穷矩：

              纠正一阶矩：

              计算参数更新量： 

  更新参数：

end while

---

9.Nadam

修改一阶矩的估计值，并将Nesterov算法和Adam算法结合起来，形成了Nadam(Nesterov-accelerated Adaptive Moment Estimation)算法。

前面我们已经看到了NAG算法的公式：

                       

Adam算法的更新公式可以展开为;

               

可以看出，两个公式的形式很相近，为了体现Nesterov的效果，只需要将公式中的修改为即可。具体算法如下：

---

参数：学习率，微小量，一阶矩，二阶矩，衰减率、

初始化：

 while 停止条件未满足do

              从训练数据中抽取m条数据{}及对应的标签{}

              计算梯度：

              更新一阶矩：

             更新一阶矩的Nesterov加速值：

             更新二阶矩：

              纠正一阶矩：

             纠正二阶矩：

              计算参数更新量： 

  更新参数：

end while

---

10.总结

以动量为核心的算法更容易在山谷型的优化曲面中找到最优解，如果优化曲面在某个方向震荡严重，而在另外一些方向趋势明显，那么基于动量的算法能够把握这种趋势，让有趋势的方向积累能量，同时让震荡的方向相互抵消。但如果趋势不够明显，那么优化参数的路径必然会存在一些绕弯的情况。

以自适应为核心的算法（Adagrad、RMSProp、Adadelta）容易在各种场景下找到平衡，对于梯度较大的一些场景，它会适当的减少更新量；对于梯度较小的一些场景，它又会适当增加更新量，所以实际上是对优化做了一定的折衷。但是对于一些场景不是很复杂的优化问题，这样的限制实际阻碍了优化的快速进行。   

所以如果数据是稀疏的，就用自适用方法，即 Adagrad, Adadelta, RMSprop, Adam。RMSprop, Adadelta, Adam 在很多情况下的效果是相似的。Adam 就是在 RMSprop 的基础上加了 bias-correction 和 momentum，随着梯度变的稀疏，Adam 比 RMSprop 效果会好。整体来讲，Adam 是最好的选择。很多论文里都会用 SGD，没有 momentum 等。SGD 虽然能达到极小值，但是比其它算法用的时间长，而且可能会被困在鞍点。如果需要更快的收敛，或者是训练更深更复杂的神经网络，需要用一种自适应的算法。

主要参考：

               《深度学习核心技术与实践》

                https://www.cnblogs.com/guoyaohua/p/8542554.html

   方向导数与梯度——学习笔记