温故知新：合并排序（merge sort）及优化方法

在学习数据结构的表时，我们经常会做到这样的一道题：将两个数组合并为一个数组，并且从低位到高位是非减的。这题不难，但这样的操作是合并排序的基本过程。合并排序的基本思想是分治，将整个的数组排序建立在其子数组的排序之上，其过程为，将数组a[1~n]划分为以单个元素为一个集合，这样就得到了n个集合，再两两集合进行合并的同时排序（就是上面提到的那道题的操作），合并完就得到了n/2（取上整）个集合，再重复合并操作直到集合个数剩下一个即a[1~n]，这时可结束合并排序。

template
void mergeAB(T a[],int l,int m,int r)
{
    T *b=new T[r-l+1];
    for(int i=l;i<=r;i++)
        b[i-l]=a[i];
    int start1=0,start2=m-l+1,start3=l;
    while(start1<=m-l && start2<=r-l)
    {
        if(b[start1]
void mergeSort(T a[],int l,int r)
{
    if(l>=r) return ;
    mergeSort(a,l,(l+r)/2);
    mergeSort(a,(l+r)/2+1,r);
    mergeAB(a,l,(l+r)/2,r);
}

对合并排序的优化主要是对其递归上进行简化。和快速排序一样，当合并排序进行递归的数组长度足够小时，可以改用插入排序，因为小规模上插入排序来得更有优势。那么，我们令当排序数组长度小于M=10时，采用插入排序，

template
void insertion(T a[],int l,int r)
{
    for(int i=l+1;i<=r;i++)
    {
        T v=a[i];
        int j=i;
        while(j>l && v
void mergeSort_M(T a[],int l,int r)
{
    if(r-l

除了减少递归次数，还有就是采用模拟递归技术，我们知道合并排序就是将元素两两合并，那么可以从数组左端开始，令步长h=1，每隔两个步长就执行一次合并，再令步长h=h+h，重复上述直到步长超过数组长度，这种方法叫自底而上合并排序（mergeBU）。

template
void mergeBU(T a[],int l,int r)
{
    for(int m=1;m

观察mergeBU发现，以步长为1为起始是因为只有一个元素的数组是有序的，那么就可以放心地进行合并。但实际上，数组的一些元素本来便是有序的，如{4,2,3,9,1,5,6}中可以由分为有序的三个部分{4},{2,3,9},{1,5,6}，这样我们只需对三个有序的进行合并排序即可，这种方法更加自然，所以称为自然合并排序。基本思想就是对数组进行一次扫描，划分为有序的部分，再进行合并排序。自然合并排序对有序的数组只需进行时间为o(n)的扫描，相对地mergeBU需要o(nlogn)。

template
void naturalMergeSort(T a[],int l,int r)
{
    while(1)
    {
        int start=l;
        int m=l;
        int end=l;
        int flag=0;
        for(int i=l+1;i<=r;i++)
        {
            if(a[i]=a[end])
            {
                end=i;
            }
        }
        mergeAB(a,start,m,end);
        if(start==l && end==r) break;
    }
}

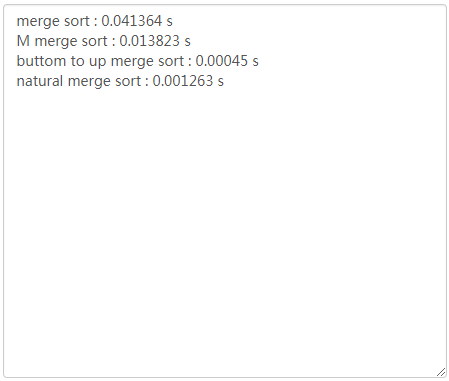
下面测试长度为十万的随机数组，元素取值范围为[1,99999]的排序时间比较结果，

template
void print(string name,void(*sortName)(T* ,int ,int ),T a[],int length){
	clock_t start=clock();
	sortName(a,0,length-1);
	clock_t end=clock();
	cout<