机器学习入门之《统计学习方法》笔记整理——感知机

  从头开始学习李航老师的《统计学习方法》，这本书写的很好，非常适合机器学习入门。
  如果部分显示格式有问题请移步Quanfita的博客查看

---

目录

---

感知机模型

  什么是感知机？感知机是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1和-1二值。感知机学习旨在求出可以将数据进行划分的分离超平面，所以感知机能够解决的问题首先要求特征空间是线性可分的，再者是二类分类，即将样本分为{+1, -1}两类。分离超平面方程为：

w⋅x+b=0 w · x + b = 0

  这样，我们就可以构建一个由输入空间到输出空间的函数：

f(x)=sign(w⋅x+b) f ( x ) = s i g n ( w · x + b )

  称为感知机。其中，w和b为感知机模型的参数， w∈Rn w ∈ R n 叫作权值（weight）， b∈R b ∈ R 叫作偏置, sign s i g n 是符号函数，即

sign(x)={+1−1 , x⩾0 , x<0 s i g n ( x ) = { + 1  ,  x ⩾ 0 − 1  ,  x < 0

  感知机模型的假设空间是定义在特征空间中的线性分类模型，即函数集合 {f∣f(x)=w⋅x+b} { f ∣ f ( x ) = w ⋅ x + b } 。

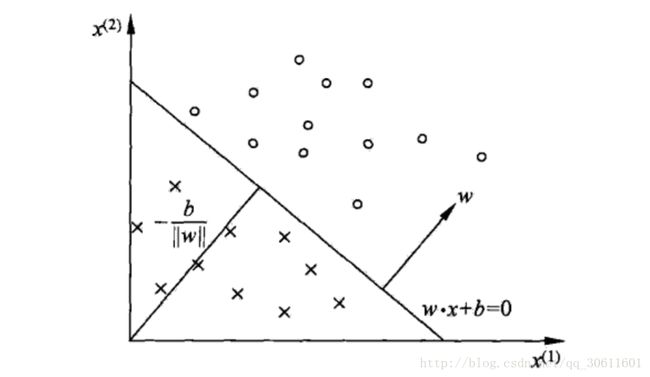
感知机学习策略

  给定一个数据集 T={(x1,y1),(x2,y2),...,(xN,yN)} T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } ，其中， xi∈X=Rn x i ∈ X = R n ， yi∈Y={+1,−1} y i ∈ Y = { + 1 , − 1 } ， i=1,2,...,N i = 1 , 2 , . . . , N 。我们假定数据集中所有 yi=+1 y i = + 1 的实例i，有 w⋅x+b>0 w ⋅ x + b > 0 ，对所有 yi=−1 y i = − 1 的实例i，有 w⋅x+b<0 w ⋅ x + b < 0 。

  先给出输入空间 Rn R n 中任意一点 x0 x 0 到超平面 S S 的距离：

−1∥w∥|(w⋅x0+b)| − 1 ‖ w ‖ | ( w ⋅ x 0 + b ) |

  这里， ∥w∥ ‖ w ‖ 是 w w 的 L2 L 2 范数。

  对于误分类数据 (xi,yi) ( x i , y i ) 来说，有

−yi(w⋅xi+b)>0 − y i ( w ⋅ x i + b ) > 0

  因此，误分类点 xi x i 到超平面 S S 的距离可以写作：

−1∥w∥yi(w⋅xi+b) − 1 ‖ w ‖ y i ( w ⋅ x i + b )

  假设超平面 S S 的误分类点的集合为 M M ,那么所有误分类点到超平面 S S 的总距离为

−1∥w∥∑xi∈Myi(w⋅xi+b) − 1 ‖ w ‖ ∑ x i ∈ M y i ( w ⋅ x i + b )

  这里 ∥w∥ ‖ w ‖ 的值是固定的，不必考虑，于是我们就可以得到感知机 sign(w⋅x+b) s i g n ( w ⋅ x + b ) 的损失函数为：

L(w,b)=−∑xi∈Myi(w⋅xi+b) L ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b )

  这个损失函数就是感知机学习的经验风险函数。

感知机学习算法

  通过上面的损失函数，我们很容易得到目标函数

minw,bL(w,b)=−∑xi∈Myi(w⋅xi+b) min w , b L ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b )

  感知机学习算法是误分类驱动的，具体采用随机梯度下降法( stochastic gradient descent )。

原始形式

  所谓原始形式，就是我们用梯度下降的方法，对参数 w w 和 b b 进行不断的迭代更新。任意选取一个超平面 w0,b0 w 0 , b 0 然后使用梯度下降法不断地极小化目标函数。随机梯度下降的效率要高于批量梯度下降 ( 参考Andrew Ng的CS229讲义, Part 1 LMS algorithm部分,翻译) 。

  假设误分类点集合 M M 是固定的，那么损失函数 L(w,b) L ( w , b ) 的梯度为

∇wL(w,b)=−∑xi∈Myixi ∇ w L ( w , b ) = − ∑ x i ∈ M y i x i

∇bL(w,b)=−∑xi∈Myi ∇ b L ( w , b ) = − ∑ x i ∈ M y i

  接下来，随机选取一个误分类点 (xi,yi) ( x i , y i ) ，对 w,b w , b 进行更新：

w←w+ηyixi w ← w + η y i x i

b←b+ηyi b ← b + η y i

  其中 η(0<η⩽1) η ( 0 < η ⩽ 1 ) 为步长，也称学习率（learning rate）。步长越长，下降越快，如果步长过长，会跨过极小点导致发散；如果步长过小，消耗时间会很长。通过迭代，我们的损失函数就不断减小,直到为0。

算法1 (感知机学习算法的原始形式)

输入: 训练数据集 T={(x1,y1),(x2,y2),...,(xn,yn)} T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } , 其中 xi∈X=Rn,yi∈Y={−1,+1},i=1,2,...,N x i ∈ X = R n , y i ∈ Y = { − 1 , + 1 } , i = 1 , 2 , . . . , N ；学习率 η(0<η⩽1) η ( 0 < η ⩽ 1 ) ；

输出: w,b w , b ；感知机模型 f(x)=sign(w⋅x+b) f ( x ) = s i g n ( w ⋅ x + b )

(1) 选取初值 w0,b0 w 0 , b 0

(2) 在训练集中选取数据 (xi,yi) ( x i , y i )

(3) 如果 yi(w⋅x+b)⩽0 y i ( w ⋅ x + b ) ⩽ 0

w←w+ηyixi w ← w + η y i x i

b←b+ηyi b ← b + η y i

(4) 转至 (2) , 直到训练集中没有错误分类点。

  这种学习算法直观上有如下解释：当一个样本被误分类时，就调整w和b的值，使超平面S向误分类点的一侧移动，以减少该误分类点到超平面的距离，直至超平面越过该点使之被正确分类。

例子：如图所示，正实例点是 x1=(3,3)T,x2=(4,3)T x 1 = ( 3 , 3 ) T , x 2 = ( 4 , 3 ) T ，负实例点是 x3=(1,1)T x 3 = ( 1 , 1 ) T ，使用感知机算法求解感知机模型 f(x)=sign(w⋅x+b) f ( x ) = s i g n ( w ⋅ x + b ) 。这里， w=(w(1),w(2)),x=(x(1),x(2)) w = ( w ( 1 ) , w ( 2 ) ) , x = ( x ( 1 ) , x ( 2 ) ) 。

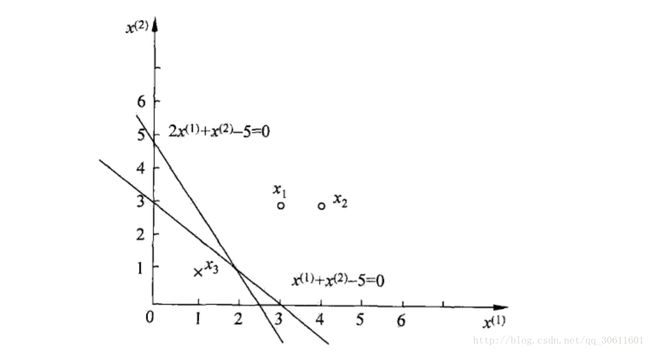
  这里我们取初值 w0=0,b0=0 w 0 = 0 , b 0 = 0 , 取 η=1 η = 1 。

Python代码如下:

train = [[(3, 3), 1], [(4, 3), 1], [(1, 1), -1]]

w = [0, 0]
b = 0

# 使用梯度下降法更新权重
def update(data):
    global w, b
    w[0] = w[0] + 1 * data[1] * data[0][0]
    w[1] = w[1] + 1 * data[1] * data[0][1]
    b = b + 1 * data[1]
    print(w, b)

# 计算到超平面的距离
def cal(data):
    global w, b
    res = 0
    for i in range(len(data[0])):
        res += data[0][i] * w[i]
    res += b
    res *= data[1]
    return res

# 检查是否可以正确分类
def check():
    flag = False
    for data in train:
        if cal(data) <= 0:
            flag = True
            update(data)
    if not flag:
        print("The result: w: " + str(w) + ", b: "+ str(b))
        return False
    flag = False

for i in range(1000):
    check()
    if check() == False:
        break

  可以得到如下结果：

[3, 3] 1
[2, 2] 0
[1, 1] -1
[0, 0] -2
[3, 3] -1
[2, 2] -2
[1, 1] -3
The result: w: [1, 1], b: -3

  如果选取的初值不同或选取不同的误分类点，我们得到的超平面也不一定相同。

算法的收敛性

  主要是证明Novikoff定理，纯数学的东西，公式要码到吐了…不过找到了一篇笔记，分享给大家《Convergence Proof for the Perceptron Algorithm》

对偶形式

  对偶形式的基本思想是，将 w w 和 b b 表示为实例 xi x i 和标记 yi y i 的线性组合形式，通过求解其系数而求得 w w 和 b b 。至于为什么…现在我还不太明白，也许以后学着学着就明白了吧。(书中提到与第七章支持向量机相对应，可能到那时候就明白了)

  假设初始值 w0,b0 w 0 , b 0 均为0，对误分类点 (xi,yi) ( x i , y i ) 通过

w←w+ηyixi w ← w + η y i x i

b←b+ηyi b ← b + η y i

  更新 w,b w , b ，假设更新次数为n次，则 w,b w , b 关于 (xi,yi) ( x i , y i ) 的增量分别为 αiyixi α i y i x i 和 αiyi α i y i ，这里 αi=niη α i = n i η ，可以得到

w=∑i=1Nαiyixi w = ∑ i = 1 N α i y i x i

b=∑i=1Nαiyi b = ∑ i = 1 N α i y i

  这里， α⩾0,i=1,2,...,N α ⩾ 0 , i = 1 , 2 , . . . , N ，当 η=1 η = 1 时，表示第 i i 个样本由于被误实例而进行的更新次数。某实例更新次数越多，表示它距离超平面 S S 越近，也就越难正确分类。换句话说，这样的实例对学习结果影响最大。

算法2 (感知机学习算法的对偶形式)

输入: 训练数据集 T={(x1,y1),(x2,y2),...,(xn,yn)} T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } , 其中 xi∈X=Rn,yi∈Y={−1,+1},i=1,2,...,N x i ∈ X = R n , y i ∈ Y = { − 1 , + 1 } , i = 1 , 2 , . . . , N ；学习率 η(0<η⩽1) η ( 0 < η ⩽ 1 ) ；

输出: α,b α , b ；感知机模型 f(x)=sign(∑j=1Nαjyjxj⋅xi+b) f ( x ) = s i g n ( ∑ j = 1 N α j y j x j ⋅ x i + b )

(1) α←0,b←0 α ← 0 , b ← 0

(2) 在训练集中选取数据 (xi,yi) ( x i , y i )

(3) 如果 yi(∑j=1Nαjyjxj⋅xi+b)⩽0 y i ( ∑ j = 1 N α j y j x j ⋅ x i + b ) ⩽ 0

α←αi+η α ← α i + η

b←b+ηyi b ← b + η y i

(4) 转至 (2) , 直到训练集中没有错误分类点。

  由于训练实例仅以内积的形式出现，为方便，可预先将训练集中实例间的内积计算出来并以矩阵形式存储，这个矩阵就是Gram矩阵。

G=[xi⋅xj]N×N G = [ x i ⋅ x j ] N × N

  还是上面的例题，这次我们用对偶形式给出答案。

import numpy as np

train = np.array([[[3, 3], 1], [[4, 3], 1], [[1, 1], -1]])

a = np.array([0, 0, 0])
b = 0
Gram = np.array([])
y = np.array(range(len(train))).reshape(1, 3)# 标签
x = np.array(range(len(train) * 2)).reshape(3, 2)# 特征

# 计算Gram矩阵
def gram():
    g = np.array([[0, 0, 0], [0, 0, 0], [0, 0, 0]])
    for i in range(len(train)):
        for j in range(len(train)):
            g[i][j] = np.dot(train[i][0], train[j][0])
    return g

# 更新权重
def update(i):
    global a, b
    a[i] = a[i] + 1
    b = b + train[i][1]
    print(a, b) 

# 计算到超平面的距离
def cal(key):
    global a, b, x, y
    i = 0
    for data in train:
        y[0][i] = data[1]
        i = i + 1
    temp = a * y
    res = np.dot(temp, Gram[key])
    res = (res + b) * train[key][1]
    return res[0]

# 检查是否可以正确分类
def check():
    global a, b, x, y
    flag = False
    for i in range(len(train)):
        if cal(i) <= 0:
            flag = True
            update(i)
    if not flag:
        i = 0
        for data in train:
            y[0][i] = data[1]
            x[i] = data[0]
            i = i + 1
        temp = a * y
        w = np.dot(temp, x)
        print("The result: w: " + str(w) + ", b: "+ str(b))
        return False
    flag = False


Gram = gram()# 初始化Gram矩阵
for i in range(1000):
    check()
    if check() == False:
        break

  我们得到如下结果，与之前得到的结果一样：

[1 0 0] 1
[1 0 1] 0
[1 0 2] -1
[1 0 3] -2
[2 0 3] -1
[2 0 4] -2
[2 0 5] -3
The result: w: [[1 1]], b: -3

小结

  总算打完了，我机器学习直接是从Tensorflow搭建神经网络入的门，以前只是对其他机器学习算法有一些了解，这次真正学起来，感觉真不容易。这最简单的感知机是最简单的机器学习算法，也是神经网络的基础。

  真心推荐李航老师的这本《统计学习方法》很棒，入门必备。

  打LeTeX公式好累啊~~~!

参考文章

1. 《李航：统计学习方法》— 感知机算法原理与实现
2. 《统计学习方法》读书笔记——感知机