最全最详细-线性规划(最小二乘、正交回归、梯度下降、仿真)

1. 问题描述

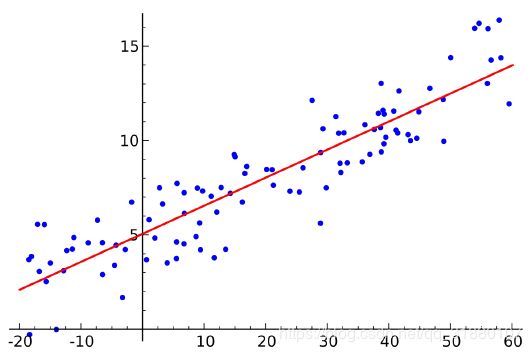
在二维平面上，给定若干个点，求一条直线能够很好的拟合这些点。如图所示。

为什么这个问题很重要？

1. 这是一个非常重要而且很常见的问题；
2. 是控制、滤波、优化、视觉、机器学习等领域的一个基础问题；
3. 涉及到很多必须的数学知识，为将来研究的研究打下基础；
4. 这是一个很好的由浅入深的问题。

本文的仿真代码请看我附带的资源。

2. 问题分析

这是一个线性拟合或者线性回归问题,目的是在二维平面上，找到一条直线来拟合给出的点。

线性拟合有很多方法，每个方法都有自己的目标函数，不同的情况下应该要使用相应的目标函数和相应的方法。每种方法都有其自己的适用范围和意义，每种方法也都有自己的优缺点。

3. 解析解法

这个问题的复杂程度还不是很大，所以能够通过数学的方法求出解析解。

3.1 一般最小二乘法

一般最小二乘是最常用的线性拟合的方法。

一般最小二乘法的目的是找到因变量$y$与自变量$x$之间的函数关系$y=f(x)$。对于本文讨论的为题，可以将点的横坐标看做自变量，将纵坐标看做因变量。然后使用一般最小二乘法找到自变量和因变量之间的函数关系，由这个函数关系可以确定一条直线，这就是拟合出来的直线。

3.1.1目标函数

假设给出的若干点的坐标为：$(x_1,y_1),(x_2,y_2)\cdots (x_n,y_n)$。定义纵坐标$y$的误差${ϵ}_i$为真值与观测值之差，定义$y$的残差${\widehat{ϵ}}_i$为估计值与观测值的差，公式如下：
$${ϵ}_i=y_i-y_i^{\star }$$

$${\widehat{ϵ}}_i=y_i-{\hat{y}}_i$$

一般最小二乘法的目的是使拟合误差（残差和）最小，也就是$\min \sum {\widehat{ϵ}}_i$ ，所以目标函数的形式如下：
$${\mathbf{J}}_1=\frac{1}{2}\sum _{i=1}^n{\widehat{ϵ}}_i^2=\frac{1}{2}\sum _{i=1}^n({\hat{y}}_i-y_i{)}^2=\frac{1}{2}(\hat{\mathbf{y}}-\mathbf{y}{)}^T(\hat{\mathbf{y}}-\mathbf{y})$$
其中$\mathbf{y}=[y_1,y_2,\cdots ,y_n{]}^T$，这里添加的$\frac{1}{2}$只是为了方便计算。

所以最小二乘法就是找到一组直线的参数，使得目标函数最小。

3.1.2 求解推导

直线方程使用斜截式直线方程：$y=kx+c$，所以要求解的直线参数为斜率$k$和截距$c$。所以有：$\widehat{y_i}=\hat{k}{x}_i+\hat{c}$。写成矩阵形式为：
$$\hat{\mathbf{y}}=\mathbf{X}\mathbf{\theta }$$
其中，$\mathbf{X}=\left[\begin{array}{cc}{x}_1& 1\\ x_2& 1\\ ⋮& ⋮\\ x_n& 1\end{array}\right]$，$\mathbf{\theta }=\left[\begin{array}{c}\hat{k}\\ \hat{c}\end{array}\right]$，将其带入目标函数${\mathbf{J}}_1$得：
$${\mathbf{J}}_1=\frac{1}{2}(\mathbf{X}\mathbf{\theta }-\mathbf{y}{)}^T(\mathbf{X}\mathbf{\theta }-\mathbf{y})$$
目标函数对 $\theta$求导，并令其等于零，得：
$$\frac{\partial }{\partial \mathbf{\theta }}{\mathbf{J}}_1={\mathbf{X}}^T(\mathbf{X}\mathbf{\theta }-\mathbf{y})=0$$
解得：
$$\mathbf{\theta }=({\mathbf{X}}^T\mathbf{X}{)}^{-1}{\mathbf{X}}^T\mathbf{y}$$
即：
$$\left[\begin{array}{c}\hat{k}\\ \hat{c}\end{array}\right]=({\mathbf{X}}^T\mathbf{X}{)}^{-1}{\mathbf{X}}^T\mathbf{y}$$

3.1.3 几何意义

从目标函数上看，一般最小二乘法的直观上的理解是：在二维平面上找到一条直线，使得每个点到直线的竖直距离之和最小。也就是说，一般最小二乘优化的是竖直距离，即纵坐标$y$的误差。

一般最小二成误差描述

上图中红色线段即为每个点的竖直误差，一般最小二乘法就是找到这样一条直线，使得红色线段的和最小。

3.1.4 缺点

3.1.4.1 对异常值很敏感

一般最小二乘法对异常值很敏感，只要一个奇怪的异常值就可能会改变最后的结果。

从其代数解法的最后结果来看，一般最小二乘法仅使用了点的均值信息和方差信息，所以仅对存在普通噪声的情况下适用，当存在异常值时，一般最小二乘法就无能为力了，此时需要其他的方法来解决。

3.1.4.2 没有考虑自变量的误差

一般最小二乘法仅考虑了因变量$y$存在误差的情况，没有考虑自变量$x$的误差，所以其应用条件有一定的限制。只有当自变量不存在偏差，或者自变量的偏差在一定范围内可以忽略不计时，才比较适用。当自变量和因变量的测量都存在偏差时，一般最小二乘法就不太合适了。

对于本文所讨论的问题：用一条直线拟合平面上的若干点。题目并没有提到这些点的来源，当这些点的横坐标的测量比较精确时，可以使用考虑使用一般最小二乘法。但是当这些点的横纵坐标都存在误差，而且都不能忽略时，一般最小二乘法就不太适用了，这时就必须考虑其他的方法了。

3.1.4.3 存在不可求解的情况

当要拟合的直线是垂直或接近垂直于$x$轴的时候，就无法求解了。垂直于$x$轴的直线，斜率无穷大，无法用斜截式直线方程表示。

从可解性的角度考虑，当直线垂直于$x$轴的时候，矩阵${\mathbf{X}}^T\mathbf{X}$是不可逆的，所以无法求出其最小二乘解。当直线接近垂直于$x$轴的时候，矩阵${\mathbf{X}}^T\mathbf{X}$接近奇异，如果直接求逆，也会导致很大的偏差。

所以当拟合的直线垂直或者接近垂直于$x$轴的时候，是不能用一般最小二乘法进行直线拟合的。

3.2 正交回归

一般最小二乘仅考虑了因变量$y$存在误差的情况，但是很多情况下，原始点的横纵坐标都会有误差存在。正交方法能够同时考虑自变量$x$和因变量$y$的误差。

3.2.1 目标函数

直线方程用点法式的形式表示，定义拟合直线经过的点坐标为$p_0=(x_0,y_0)$，直线的法向量为$\mathbf{v}$，这里我们假设直线的法向量为单位向量。所以可以使用两个向量$(p_0,\mathbf{v})$来表示一条直线，而且是二维平面上的任意直线。

正交回归的目的是点到直线的距离之和最小，也就是点到直线上投影点的距离最短。点到投影点的距离可以用向量${\mathbf{p}}_i=(p_i-p_0)$向直线法向量$\mathbf{v}$方向上的投影的模长来表示。

向$\mathbf{v}$投影的投影矩阵为$\mathbf{v}{\mathbf{v}}^T$。

所以目标函数可以表示为：
$${\mathbf{J}}_2=\frac{1}{2n}\sum ||\mathbf{v}{\mathbf{v}}^T(p_i-p_0)|{|}^2$$
这里的$\frac{1}{2n}$是为了计算方便。

也可以化简为几种不同的形式：
$$\begin{array}{rl}{\mathbf{J}}_2& =\frac{1}{2n}\sum {\mathbf{v}}^T(p_i-p_0)(p_i-p_0{)}^T\mathbf{v}\\ {\mathbf{J}}_2& =\frac{1}{2n}\sum [{\mathbf{v}}^T(p_i-p_0){]}^2\end{array}$$

3.2.2 求解推导

目标函数${\mathbf{J}}_2$对$p_0$求导，得：
$$\frac{d{\mathbf{J}}_2}{d{p}_0}=\frac{d}{p_0}\{\frac{1}{2n}\sum [{\mathbf{v}}^T(p_i-p_0){]}^2\}=-{\mathbf{v}}^T(\frac{\sum p_i}{n}-p_0)\mathbf{v}$$
令$\frac{d{\mathbf{J}}_2}{d{p}_0}=0$，得：
$${\mathbf{v}}^T(\bar{p}-p_0)\mathbf{v}=0$$
其中$\bar{p}$为所有拟合点的质心。

因为法向量不是零向量，所以可以得出：
$${\mathbf{v}}^T(\bar{p}-p_0)=0$$
所以，$\bar{p}$一定是直线上的一点，所以不妨设$p_0=\bar{p}$。

此时目标函数可以化简：
$${\mathbf{J}}_2=\frac{1}{2n}\sum {\mathbf{v}}^T(p_i-\bar{p})(p_i-\bar{p}{)}^T\mathbf{v}=\frac{1}{2n}{\mathbf{v}}^T\mathbf{S}\mathbf{v}$$
其中$\mathbf{S}=\sum (p_i-\bar{p})(p_i-\bar{p}{)}^T$

这是一个二次型，所以当$\mathbf{v}$取矩阵$\mathbf{S}$最小特征值对应的特征向量时，目标函数的值最小。

3.2.3 结果总结

$p_0$为拟合点的质心坐标。

$\mathbf{v}$应该取矩阵$\mathbf{S}=\sum (p_i-\bar{p})(p_i-\bar{p}{)}^T$最小特征值对应的特征向量。

3.2.4 几何意义

从正交回归的直观上的理解是：在二维平面上找到一条直线，使得每个点到直线的垂直距离之和最小。也就是说，正交回归优化的是垂直距离。

正交回归误差描述

上图中红色线段即为每个点的竖直误差，正交回归就是找到这样一条直线，使得红色线段的和最小。

4 数值解法

前面两种方法都是解析法，能够准确地求出具体值，但是如果矩阵的规模很大，用计算机求解就有些得不偿失（尤其是矩阵求逆），甚至最后的结果是错误的。

4.1 梯度下降法

梯度下降法是一个很好的方法，用计算机去迭代近似，能够达到很快的收敛速度，同时也能保证比较高的精确度。

梯度下降法的基本思想可以类比为一个下山的过程，每次循环都已当前位置为基准，找到当前这个位置最陡峭的方向，然后朝着这个方向往下走，最终就会抵达山底。对于算法来说，一个关键的点是如何找到最陡峭的方向。而且每次循环的频率也是一个关键点的参数，如果频率太高，则会收敛太慢，如果频率太低，则可能会偏离方向。

梯度下降法相当于一种迭代算法，先随机给定一个解，然后循环迭代，每次都以目标函数下降最快的

4.1.1 迭代公式

将梯度下降的思想应用到一般最小二乘中。将一般最小二乘的目标函数作为梯度下降的损失函数，将直线的点法式方程中的参数作为梯度下降的优化量。
这里为了方便，对损失函数做一个简单的变换，对损失函数除以$n$：
$${\mathbf{J}}_1=\frac{1}{2n}\sum (k{x}_i+c-y_i{)}^2$$
则迭代公式为：
$${\mathbf{\theta }}_{new}={\mathbf{\theta }}_{old}-\alpha \frac{d}{d\mathbf{\theta }}{\mathbf{J}}_3(\mathbf{\theta })$$
其中$\alpha$为步长。

4.1.2 算法步骤

线性拟合梯度下降法的迭代步骤如下：

---

Algorithm 1: 最小二乘梯度下降算法

---

输入：

​ 数据点：$(x_1,y_1),(x_2,y_2),\cdots ,(x_n,y_n)$；

输出：

​ 直线参数：斜率$k$和截距$c$；

1. 初始化直线参数，令$\mathbf{\theta }=\left[\begin{array}{c}k\\ c\end{array}\right]=\left[\begin{array}{c}1\\ 1\end{array}\right]$;
2. 初始化步长，令$\alpha =0.1$;
3. 计算梯度$\Delta =\frac{d}{d\mathbf{\theta }}{\mathbf{J}}_1(\mathbf{\theta })$;
4. while $\Delta >10^{-5}$ do
   1. 更新直线参数$\mathbf{\theta }\leftarrow \mathbf{\theta }-\alpha \Delta$;
   2. 更新梯度$\Delta =\frac{d}{d\mathbf{\theta }}{\mathbf{J}}_1(\mathbf{\theta })$;
5. end

---

4.1.3 收敛性证明

目标函数的梯度计算为：
$$\frac{d{\mathbf{J}}_1(\mathbf{\theta })}{d\mathbf{\theta }}={\mathbf{A}}^T(\mathbf{A}\mathbf{\theta }-\mathbf{y})$$
所以迭代公式可以写成：
$${\mathbf{\theta }}_{new}={\mathbf{\theta }}_{old}-\alpha {\mathbf{A}}^T(\mathbf{A}\mathbf{\theta }-\mathbf{y})$$
定义收敛值为${\mathbf{\theta }}^{\ast }$，通过解析解法，我们知道：
$${\mathbf{\theta }}^{\ast }=({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T\mathbf{y}$$
定义第$k$步的结果与收敛值的差为：
$${\mathbf{e}}_k={\mathbf{\theta }}_k-{\mathbf{\theta }}^{\ast }$$
将${\mathbf{\theta }}_k={\mathbf{e}}_k+{\mathbf{\theta }}^{\ast }$和${\mathbf{\theta }}_{k+1}={\mathbf{e}}_{k+1}+{\mathbf{\theta }}^{\ast }$带入迭代公式，得：
$$\begin{array}{rl}{\mathbf{e}}_{k+1}+{\mathbf{\theta }}^{\ast }& ={\mathbf{e}}_k+{\mathbf{\theta }}^{\ast }-\alpha {\mathbf{A}}^T(\mathbf{A}{\mathbf{e}}_k+\mathbf{A}{\theta }^{\ast }-\mathbf{y})\\ & ={\mathbf{e}}_k+\mathbf{\theta }-\alpha {\mathbf{A}}^T\mathbf{A}{\mathbf{e}}_k\end{array}$$
因此，
$${\mathbf{e}}_{k+1}=(\mathbf{I}-\alpha {\mathbf{A}}^T\mathbf{A}){\mathbf{e}}_k$$
所以，当$\alpha$足够小，使得$\mathbf{I}-\alpha {\mathbf{A}}^T\mathbf{A}$小于1的时候，结果是收敛的。

5 仿真对比

因为不同的算法不同的目标函数适用不同的情况，所以根据目标函数的不同，生成两种数据集。

5.1 原始数据采集

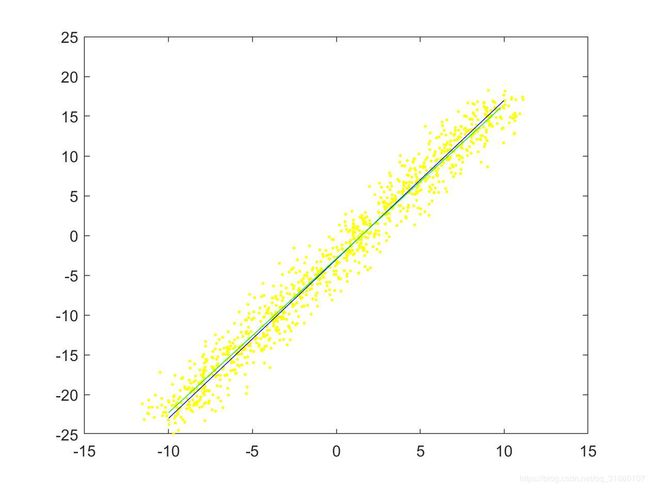
使用$-2x+y+3=0$当做原始直线方程，在直线上随机采取1000个点，然后对这些点的横纵坐标加正态分布的噪声。在这里，我们分两种情况来采集数据集，第一种情况只对纵坐标加噪声，第二种情况对横纵坐标同时加噪声。

采集后的数据点集如下图所示：

(a) 数据集1：只对$y$加噪声	(b)数据集2：同时对$x$和$y$加噪声

图，加噪声后的点和原始直线

上图中，原始直线用蓝色的直线表示，添加噪声后的点用黄色的点表示。明显可以看出，同时对$x$和$y$添加噪声后的点要相对稀疏一些。

5.2 仿真结果对比与分析

用截距式直线方程来表示，原直线方程为：$y=2x-3$。所以原直线方程的参数为：
$$\begin{array}{rl}k& =2\\ c& =-3\end{array}$$

5.2.1 仿真结果对比

首先列出三种算法求出的直线方程的参数，如下表所示：

表1：三种算法的仿真结果

	使用数据集1	使用数据集2
一般最小二乘	$k=2.0010,c=-2.9709$	$k=1.9386,c=-2.9061$
正交回归	$k=2.0130,c=-2.9708$	$k=1.9926,c=-2.9038$
梯度下降法	$k=2.0010,c=-2.9709$	$k=1.9386,c=-2.9061$

表2：三种算法的结果误差

	使用数据集1	使用数据集2
一般最小二乘	$e_k=0.0010,e_c=0.0291$	$e_k=0.0614,e_c=0.0939$
正交回归	$e_k=0.0130,e_c=0.0292$	$e_k=0.0074,e_c=0.0962$
梯度下降法	$e_k=0.0010,e_c=0.0291$	$e_k=0.0614,e_c=0.0939$

5.2.2 仿真结果分析

从上面的结果可以得出如下结论：

1. 一般最小二乘法更适用于只有$y$有噪声的情况；
2. 正交回归更适用于$x$和$y$同时包含噪声的情况；
3. 梯度下降法，因为其损失函数和一般最小二乘法相同，所以结果也是一致的。

5.2.3 拟合直线图对比

三种方法的拟合直线图如下所示：

(a)使用数据集1(只对$y$加噪声)	(b)使用数据集2(同时对$x$和$y$加噪声)

图，一般最小二乘法的仿真结果

(a) 使用数据集1(只对$y$加噪声)	(b)使用数据集2(同时对$x$和$y$加噪声)

图，正交回归仿真结果

(a)使用数据集1(只对加噪声)	(b)使用数据集2(同时对和加噪声)

图，梯度下降法仿真结果

上图中，原始直线用蓝色直线表示，原始拟合点用黄色的点表示，拟合后的直线用绿色的直线表示。

5.3 曲线采点仿真

使用$y=(x+5{)}^2$作为原始曲线，随机采点，并对$x$和$y$都加噪声。分别使用最小二乘法和正交回归进行拟合仿真，结果如下：

(a)使用一般最小二乘法	(b)使用正交回归

图，用直线拟合曲线上的点

从结果看，两种算法的最后结果差别较大。

6 向高维推广

6.1 3维空间中的平面拟合

3维空间中的平面同样可以用点法式来进行表示。我们用$(p_0,\mathbf{v})$这样的组合来表示直线，其中$p_0$表示平面上的点，$\mathbf{v}$表示平面的法向量。

则目标函数可以写成:
$${\mathbf{J}}_4=\frac{1}{2n}\sum ||\mathbf{v}{\mathbf{v}}^T(p_i-p_0)|{|}^2$$

这个跟2维直线拟合是一样的，只是向量和矩阵都多了一维。

直接写出结果：
$p_0$为拟合点的质心点坐标; $\mathbf{v}$应该取矩阵$\mathbf{S}=\sum (p_i-\bar{p})(p_i-\bar{p}{)}^T$最小特征值对应的特征向量。

6.2 3维空间中的直线拟合

3维空间中的直线可以用点向式来表示。用$(p_0,\mathbf{v})$这样的组合来表示3维空间中的任意一条直线，其中$p_0$表示直线上的一点，$\mathbf{v}$为直线的方向向量，因为只表示方向，其大小没有关系，所以直接定义其为单位向量。则，点到直线的投影距离为：
$$d_i=||(\mathbf{I}-\mathbf{v}{\mathbf{v}}^T)(p_i-p_0)||$$

目标函数可以写成：
$${\mathbf{J}}_5=\frac{1}{2n}\sum ||(\mathbf{I}-\mathbf{v}{\mathbf{v}}^T)(p_i-p_0)|{|}^2$$

也可以化简为多种形式：
$$\begin{array}{rl}{\mathbf{J}}_5& =\frac{1}{2n}\sum [(p_i-p_0{)}^T(\mathbf{I}-\mathbf{v}{\mathbf{v}}^T)(p_i-p_0)]\\ {\mathbf{J}}_5& =\frac{1}{2n}\sum [(p_i-p_0{)}^T(p_i-p_0)-{\mathbf{v}}^T(p_i-p_0)(p_i-p_0{)}^T\mathbf{v}]\end{array}$$

推导过程：
目标函数对$p_0$求导得：
$$\frac{\partial {\mathbf{J}}_5}{\partial p_0}=-\frac{1}{n}\sum (\mathbf{I}-\mathbf{v}{\mathbf{v}}^T)(p_i-p_0)$$

令$\frac{\partial {\mathbf{J}}_5}{\partial p_0}=0$得：
$$p_0=\bar{p}$$

其中$\bar{p}$为拟合点的质心。

此时，目标函数重写为：
$${\mathbf{J}}_5=\frac{1}{2n}\sum (p_i-\bar{p}{)}^T(p_i-\bar{p})-\frac{1}{2n}\sum {\mathbf{v}}^T(p_i-\bar{p})(p_i-\bar{p}{)}^T\mathbf{v}$$

所以为了求${\mathbf{J}}_5$的最小值，应该求${\mathbf{J}}_Q=\frac{1}{2n}\sum {\mathbf{v}}^T(p_i-\bar{p})(p_i-\bar{p}{)}^T\mathbf{v}$的最大值。

所以$\mathbf{v}$应该取矩阵$\mathbf{S}=\sum (p_i-\bar{p})(p_i-\bar{p}{)}^T$最大特征值对应的特征向量。