Python数据处理(三)——美国西雅图自行车流量可视化
目的:熟悉时间序列数据的处理方法和时间序列的使用,并用可视化展示出来。
下载数据:可以通过复制链接下载;也可以通过软件直接下载,下载文件存放在当前工作目录下。数据来源:#下载数据 !curl -o FremontBridge.csv https://data.seattle.gov/api/views/65db-xm6k/rows.csv?accessType=DOWNLOAD
代码:
!curl -o FremontBridge.csv https://data.seattle.gov/api/views/65db-xm6k/rows.csv?accessType=DOWNLOAD前两章已经提到过数据处理的基本步骤,在此不做过多的陈述。基本是导入模块和读取数据形成数据框。
#导入模块
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn
data = pd.read_csv('FremontBridge.csv', index_col='Date', parse_dates=True)
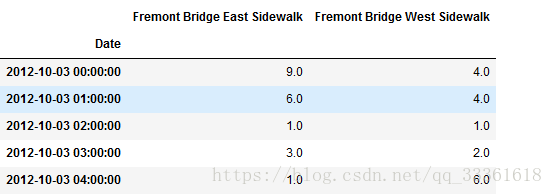
data.head()数据显示的前五行:
由于该列名较长,不便于之后的计算和数据查看,所以对列名进行重命名。并且计算东、西方向的总和,使用到df.eval()函数,该函数在Python数据统计分析和数据处理过程中使用较多,对该函数进行基本介绍。
函数:data.eval(expr, inplace=False, **kwargs)
参数说明:expr:表达式 str类型,可接受算术运算符(+/-等)、比较运算符(>/
inplace:Boolean 类型,主要是为了表示是否在原数据框上进行修改,默认为否
代码:
data.columns #查看数据框列名
data.columns = ['East', 'West'] #数据框重命名列名,该名称可以命名为中文
#法一:直接计算
data['Total'] = data.East + data.West #新增总和列
#法二:引用表达式计算函数
data['Total'] = data.eval('East + West')
#等同于 data.eval('Total = East + West', inplace= True)数据处理结果差不多完成了,执行data.dropna().describe()函数,查看数据基本统计信息
用所有数据绘制图形。
seaborn.set()
data.plot()
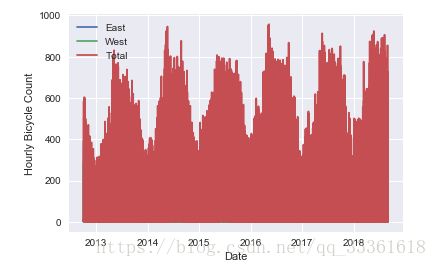
plt.ylabel('Hourly Bicycle Count')结果:
结论:该图形的数据量较大,导致不能直观的观察结果。所以考虑绘制每周的自行车流量图形。
代码如下:
#重新取样,按周统计
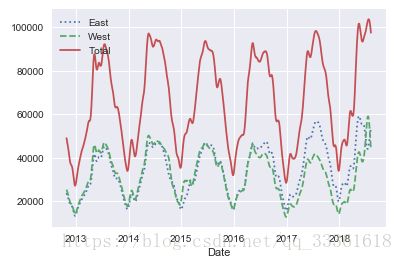
weekly = data.resample('W').sum()
weekly.plot(style=[':','--','-'])
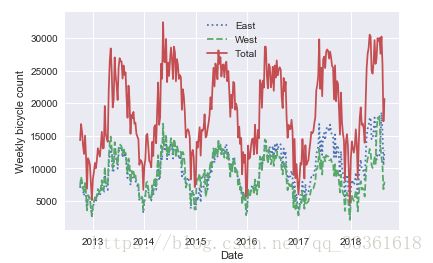
plt.ylabel('Weekly bicycle count')显示结果:
结论:用每周的自行车流量绘图,图像显示还是不够平滑,考虑到按日统计30天的移动平均。
移动平均是时间序列数据中使用到的一个重要计算方式,还有加权平均以及其他平均,初略介绍这类方法。
- 移动平均介绍:时间序列数据中通常包含有趋势性变动和周期性变动两种变动因素,周期性变动因素往往会掩盖数据的趋势性变动规律,通过对数据进行移动平均处理可有效反映出数据的趋势性变动规律。
- 处理方法为,针对时间序列中的每个数据,求该数据与之前若干个数据的平均值,由各点处的平均值形成一组新的时间序列数据,其将反映出原时间序列数据的整体变化趋势。
调用函数:
- df.rolling(window, min_periods=None, freq=None, center=False, win_type=None, on=None, axis=0, closed=None)
部分参数说明:
- window:表示时间窗的大小,注意有两种形式(int or offset)。如果使用int,则数值表示计算统计量的观测值的数量即向前几个数据。如果是offset类型,表示时间窗的大小。
- min_periods:最少需要有值的观测点的数量,对于int类型,默认与window相等。对于offset类型,默认为1。
- center:是否使用window的中间值作为label,默认为false。只能在window是int时使用。
代码:
#计算数据30日的移动平均
daily = data.resample('D').sum()
daily.rolling(30, center=True).mean().plot(style=[':','--','-'])
plt.ylabel('mean of 30 days count')
#获得平滑图像
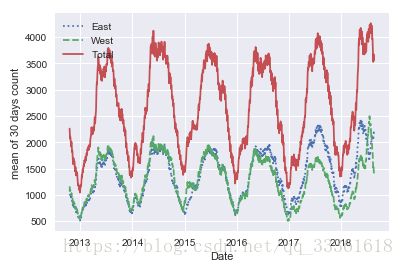
daily.rolling(50, center=True, win_type='gaussian').sum(std=10).plot(style=[':','--','-'])图像展示:
结论:该自行车流量在年代中具有明显的周期性特征。
然后考虑自行车流量在一天之内的周期性特征,代码如下:
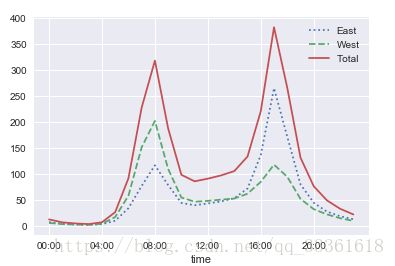
by_time = data.groupby(data.index.time).mean()
hourly_tricks = 4 * 60 * 60 * np.arange(6)
by_time.plot(xticks=hourly_tricks, style=[':','--','-'])图像显示:
结论:一周之中,自行车流量最多在8:00-10:00、17:00-18:00,即上下班高峰期时间段。
进而观察一周之内的人流量情况,工作日与节假日的自行车流量的区别。代码如下:
by_weekday = data.groupby(data.index.dayofweek).mean()
xticks = ['','Mon','Tues','Wed','Thurs','Fri','Sat','Sun']
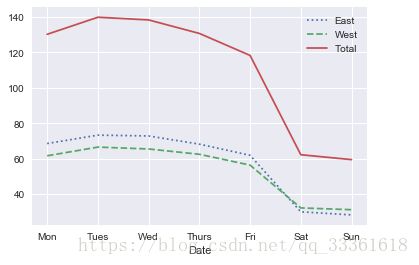
by_weekday.plot(style=[':','--','-'])
# plt.xticks = by_weekday.index
plt.gca().set_xticklabels(xticks)图像:
结论:工作日西雅图大桥自行车流量明显高于休息日。
然而,从上图来看,受工作日自行车流量影响,之前一天中自行车流量的周期性特征不能代表休息日车流量的周期性特征。所以对工作日和休息日的数据分别进行观察。
使用到np.where(判断条件, '命名值1', '命名值2'), 命名值1代表True的值,命名值2代表False的值。
相当于代码:
data['weekend'] = 'weekend'
data['weekend'][data.index.weekday < 5] = 'weekday'代码:
#工作日和休息日每小时的数据
weekend = np.where(data.index.weekday < 5, 'Weekday', 'Weekend')#where作为条件选择
by_time = data.groupby([weekend, data.index.time]).mean()
fig, ax = plt.subplots(1, 2, figsize=(14, 5))
by_time.ix['Weekday'].plot(ax=ax[0], title='Weekdays',
xticks=hourly_tricks, style=[':','--','-'])
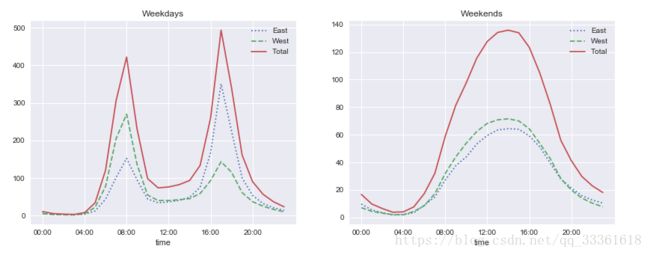
by_time.ix['Weekend'].plot(ax=ax[1], title='Weekends',
xticks=hourly_tricks, style=[':','--','-'])图像:
结论:工作日在上下班时间出现峰值,而休息日白天的周期性特征不明显。