HHT变换

将数据先进行fast-ICA处理，再进行滤波之后得到的数据，进行HHT变换。
导入库：

import numpy as np
import pyhht    #pyhht库，进行hht变换的主要库，可使用pip install pyhht安装
import matplotlib.pyplot as plt
from pyhht.visualization import plot_imfs    #同pyhht库，可视化操作
import tftb.processing    #用来计算瞬时频率的包
from scipy.signal import hilbert    #hilbert变换需要使用的包

导入数据：

LoadList = ["EEG-Logs/2-滤波后/EEG_1_0.txt", "EEG-Logs/2-滤波后/EEG_1_2.txt", "EEG-Logs/2-滤波后/EEG_1_3.txt"]   #由于可能需要导入多个数据，故使用List表示
Data = np.loadtxt(LoadList[0], delimiter=',')   #data为一个(263,14)的数组

进行hht处理：

DataRaw = Data[:, 0]  # 原信号
decomposer = pyhht.emd.EMD(DataRaw)
imfs = decomposer.decompose()      #获取到imfs数据。

画图：

plot_imfs(DataRaw, imfs)    #得到7张图，一张原数据，一张IMF以及rn数据

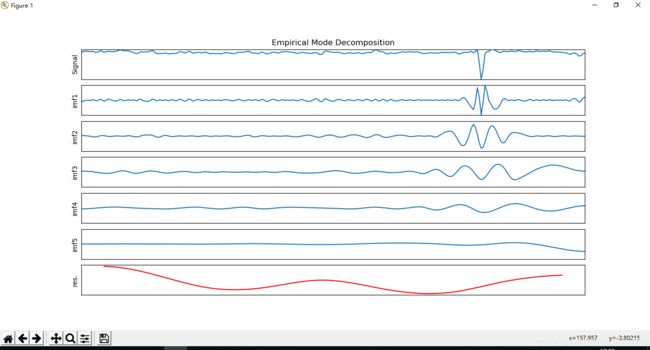
再使用matplotlib库的画图可以知道imfs[5,:]就是rn

for i in range(6):
    plt.subplot(6, 1, i + 1)
    plt.plot(imfs[i, :])
plt.show()

根据hht的原理，可以知道，原始信号x(t)可以有如下表达：
$x(t)={\sum }_{i=1}^n{c}_i(t)+r_n(t)$
根据上图可知，ifms这个数组里面的前5行代表 $c_i(t)$，即IMF分量，最后1行代表$r_n(t)$，即剩余信号。
理论上如此，但是实际上把IMF和剩余信号相加，最后减去原信号，还是有一定的误差。误差如下：

rn = DataRaw - ImfSum  # 误差
plt.plot(rn)
plt.show()

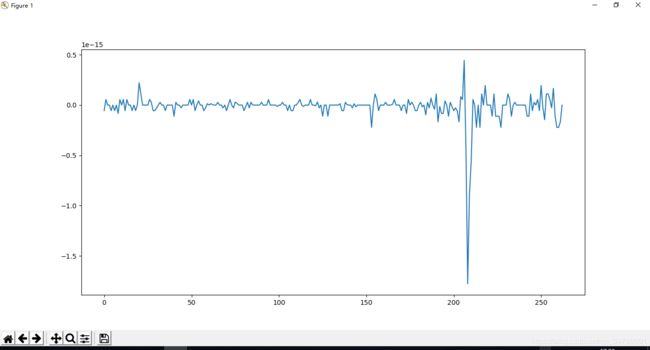
可以看到，误差为$1^{-15}$级别。

接下来要对数据IMF分量进行HT变换。

ReImf0 = hilbert(imfs[0])
ReImf1 = hilbert(imfs[1])
ReImf2 = hilbert(imfs[2])
ReImf3 = hilbert(imfs[3])
ReImf4 = hilbert(imfs[4])
ReImf = np.array([ReImf0, ReImf1, ReImf2, ReImf3, ReImf4])

变换之后放进ReImf数组里面。

amplitude = abs(ReImf0)     #计算幅值
instf, timestamps = tftb.processing.inst_freq(ReImf0)    #计算瞬时频率
plt.plot(timestamps, instf)     #画图看看效果
plt.show()

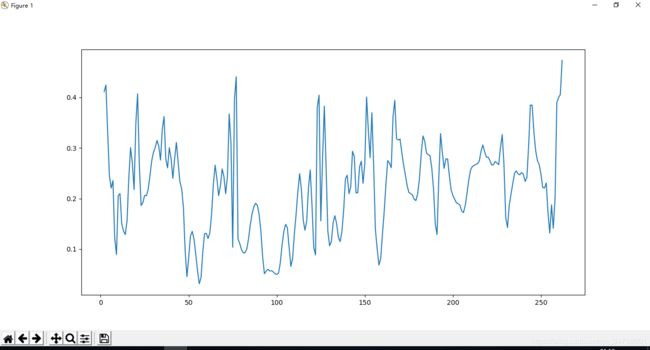
至此，HHT变换完毕，接下来要对获得的IMF0和IMF1构建AR参数，书上推荐使用Yule-Walker方程，但是我不会。。。网上找了最小二乘法的代码，放了进来

def ar_least_square(sample, p):
    matrix_x = np.zeros((sample.size - p, p))
    matrix_x = np.matrix(matrix_x)
    array = sample.reshape(sample.size)
    j = 0
    for i in range(sample.size - p):
        matrix_x[i, 0:p] = array[j:j + p]
        j = j + 1
    matrix_y = np.array(array[p:sample.size])
    matrix_y = matrix_y.reshape(sample.size - p, 1)
    matrix_y = np.matrix(matrix_y)
    # cofe为AR系数
    cofe = np.dot(np.dot((np.dot(matrix_x.T, matrix_x)).I, matrix_x.T), matrix_y)
    return np.array(cofe)

返回AR系数

def cal(DataRaw):
    DataRaw = DataRaw  # 原信号
    decomposer = pyhht.emd.EMD(DataRaw)
    imfs = decomposer.decompose()
    ReImf0 = hilbert(imfs[0])
    ReImf1 = hilbert(imfs[1])
    ReImf2 = hilbert(imfs[2])
    ReImf3 = hilbert(imfs[3])
    ReImf4 = hilbert(imfs[4])
    instf0, timestamps0 = tftb.processing.inst_freq(ReImf0)
    instf1, timestamps1 = tftb.processing.inst_freq(ReImf1)
    instf2, timestamps2 = tftb.processing.inst_freq(ReImf2)
    instf3, timestamps3 = tftb.processing.inst_freq(ReImf3)
    instf4, timestamps4 = tftb.processing.inst_freq(ReImf4)
    IA0 = abs(ReImf0)
    IA1 = abs(ReImf1)
    instf = np.array([instf0, instf1, instf2, instf3, instf4])  # 频率均值
    AR0 = ar_least_square(IA0, 4)
    AR1 = ar_least_square(IA1, 4)
    f1 = instf.mean()
    return np.vstack((AR0, AR1, f1))    #纵向拼接

然后把前面部分的代码写成函数，并且把AR0，AR1，f1，组成一个(9,1)的向量，其中f1本来应该使用
$IE(t)={\int }_{\omega 1}^{\omega 2}{H}^2(\omega ,t)d\omega$
公式计算的，但是找不到计算这个的库，于是把频率取了平均值组成了向量。。。

val0 = np.zeros((126,1))
val1 = np.zeros((126,1))
val2 = np.zeros((126,1))
Data = np.loadtxt(LoadList[0], delimiter=',')
for i in range(14):
    val0[9 * i:9 * i + 9] = cal(Data[:, i])

Data = np.loadtxt(LoadList[1], delimiter=',')
for i in range(14):
    val1[9 * i:9 * i + 9] = cal(Data[:, i])

Data = np.loadtxt(LoadList[2], delimiter=',')
for i in range(14):
    val2[9 * i:9 * i + 9] = cal(Data[:, i])

val=np.hstack((val0,val1,val2))    #横向拼接
print(val)
plt.plot(val[:,0])
plt.plot(val[:,1])
plt.plot(val[:,2])
plt.show()

感觉差了很多。然后把这个126*3的数组存一下

np.savetxt("EEG-Logs/3-特征提取后/EEG1.txt", val, delimiter=',')