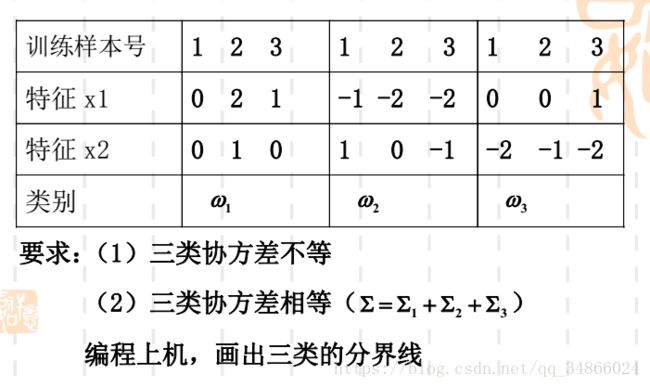
模式识别设计（Python编程）：正态分布的Bayes分类器

题目：话不多说。

代码：

import numpy as np
import math
import matplotlib.pyplot as plt

a = np.array([[0, 2, 1],
              [0, 1, 0]], dtype=np.float64)
b = np.array([[-1, -2, -2],
              [1, 0, -1]], dtype=np.float64)
c = np.array([[0, 0, 1],
              [-2, -1, -2]], dtype=np.float64)
input = [[-2], [2]]
a_t = np.matrix(a)
a_cov = np.matrix(np.cov(a_t))
a_cov_m = np.linalg.det(np.cov(a_t))
a_cov_I = a_cov.I
u1 = np.array([[1],
              [1/3]], dtype=np.float64)
g_a = -1/2 * np.matrix(input-u1).T * a_cov_I * np.matrix(input-u1) - 1/2 * math.log(abs(a_cov_m)) + math.log(1/3)
v_1 = -1/2 * a_cov_I
w_1 = a_cov_I * u1
w_10 = -1/2 * np.matrix(u1).T * a_cov_I * u1 - 1/2 * math.log(abs(a_cov_m)) + math.log(1/3)

b_t = np.matrix(b)
b_cov = np.matrix(np.cov(b_t))
b_cov_m = np.linalg.det(np.cov(b_t))
b_cov_I = b_cov.I
u2 = np.array([[-5/3],
              [0]], dtype=np.float64)
g_b = -1/2 * np.matrix(input-u2).T * b_cov_I * np.matrix(input-u2) - 1/2 * math.log(abs(b_cov_m)) + math.log(1/3)
v_2 = -1/2 * b_cov_I
w_2 = b_cov_I * u2
w_20 = -1/2 * np.matrix(u2).T * b_cov_I * u2 - 1/2 * math.log(abs(b_cov_m)) + math.log(1/3)

c_t = np.matrix(c)
c_cov = np.matrix(np.cov(c_t))
c_cov_m = np.linalg.det(np.cov(c_t))
c_cov_I = c_cov.I
u3 = np.array([[1/3],
              [-5/3]], dtype=np.float64)
g_c = -1/2 * np.matrix(input-u3).T * c_cov_I * np.matrix(input-u3) - 1/2 * math.log(abs(c_cov_m)) + math.log(1/3)
v_3 = -1/2 * c_cov_I
w_3 = c_cov_I * u3
w_30 = -1/2 * np.matrix(u3).T * c_cov_I * u3 - 1/2 * math.log(abs(c_cov_m)) + math.log(1/3)

print('协方差不等的情况下:')
print('g(1):', g_a)
print('g(2):', g_b)
print('g(3):', g_c)
if(g_a > g_b and g_a > g_c):
    print('在协方差不等的情况下,(-2, 2)属于第一类')
if(g_b > g_a and g_b > g_c):
    print('在协方差不等的情况下,(-2, 2)属于第二类')
if(g_c > g_a and g_c > g_b):
    print('在协方差不等的情况下,(-2, 2)属于第三类')
v12 = v_1 - v_2
w12 = w_1 - w_2
v23 = v_2 - v_3
w23 = w_2 - w_3
v13 = v_1 - v_3
w13 = w_1 - w_3
print("协方差矩阵不等情况下，12分界线方程为：%f x1^2 + %f x2^2 + %f x1*x2 + %f x1 + %f x2 + %f = 0" % (v12[0, 0], v12[1, 1], v12[0, 1] + v12[1, 0],
                                                                          w12[0, 0], w12[1, 0], w_10-w_20))
print("协方差矩阵不等情况下，23分界线方程为：%f x1^2 + %f x2^2 + %f x1*x2 + %f x1 + %f x2 + %f = 0" % (v23[0, 0], v23[1, 1], v23[0, 1] + v23[1, 0],
                                                                          w23[0, 0], w23[1, 0], w_20-w_30))
print("协方差矩阵不等情况下，13分界线方程为：%f x1^2 + %f x2^2 + %f x1*x2 + %f x1 + %f x2 + %f = 0" % (v13[0, 0], v13[1, 1], v13[0, 1] + v13[1, 0],
                                                                          w13[0, 0], w13[1, 0], w_10-w_30))

all_cov = a_cov + b_cov + c_cov
all_cov_I = all_cov.I
w1_all = all_cov_I * u1
w_10_all = -1/2 * np.matrix(u1).T * all_cov_I * u1 + math.log(1/3)
g_all_a = -1/2 * np.matrix(input-u1).T * all_cov_I * np.matrix(input-u1) + math.log(1/3)

w2_all = all_cov_I * u2
w_20_all = -1/2 * np.matrix(u2).T * all_cov_I * u2 + math.log(1/3)
g_all_b = -1/2 * np.matrix(input-u2).T * all_cov_I * np.matrix(input-u2) + math.log(1/3)

w3_all = all_cov_I * u3
w_30_all = -1/2 * np.matrix(u3).T * all_cov_I * u3 + math.log(1/3)
g_all_c = -1/2 * np.matrix(input-u3).T * all_cov_I * np.matrix(input-u3) + math.log(1/3)
print('协方差相等的情况下:')
print('g(1):', g_all_a)
print('g(2):', g_all_b)
print('g(3):', g_all_c)
if(g_all_a > g_all_b and g_all_a > g_all_c):
    print('在协方差相等的情况下,(-2, 2)属于第一类')
if(g_all_b > g_all_a and g_all_b > g_all_c):
    print('在协方差相等的情况下,(-2, 2)属于第二类')
if(g_all_c > g_all_a and g_all_c > g_all_b):
    print('在协方差相等的情况下,(-2, 2)属于第三类')

w12_all = w1_all - w2_all
w23_all = w2_all - w3_all
w13_all = w1_all - w3_all
print("协方差矩阵相等情况下，12分界线方程为： %f x1 + %f x2 + %f = 0" % (w12_all[0, 0], w12_all[1, 0], w_10_all-w_20_all))
print("协方差矩阵相等情况下，23分界线方程为： %f x1 + %f x2 + %f = 0" % (w23_all[0, 0], w23_all[1, 0], w_20_all-w_30_all))
print("协方差矩阵相等情况下，13分界线方程为： %f x1 + %f x2 + %f = 0" % (w13_all[0, 0], w13_all[1, 0], w_10_all-w_30_all))

#  绘图
'''x = np.arange(-10.1, 10.1, .01)
y = np.arange(-10.1, 10.1, .01)
x, y = np.meshgrid(x, y)
#  绘制协方差不等情况下的分界线
f12 = (v12[0, 0])*(x**2) + (v12[1, 1])*(y**2) + (v12[0, 1] + v12[1, 0])*(x*y) + w12[0, 0]*x + w12[1, 0]*y + (w_10-w_20)
f23 = (v23[0, 0])*(x**2) + (v23[1, 1])*(y**2) + (v23[0, 1] + v23[1, 0])*(x*y) + w23[0, 0]*x + w23[1, 0]*y + (w_20-w_30)
f13 = (v13[0, 0])*(x**2) + (v13[1, 1])*(y**2) + (v13[0, 1] + v13[1, 0])*(x*y) + w13[0, 0]*x + w13[1, 0]*y + (w_10-w_30)
# 作图
plt.figure()
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('When their covs is not equal')
plt.contour(x, y, f12, 0, colors='black')
plt.contour(x, y, f23, 0, colors='red')
plt.contour(x, y, f13, 0, colors='blue')
#  绘制协方差相等情况下的分界线
g12 = w12_all[0, 0]*x + w12_all[1, 0]*y + (w_10_all-w_20_all)
g23 = w23_all[0, 0]*x + w23_all[1, 0]*y + (w_20_all-w_30_all)
g13 = w13_all[0, 0]*x + w13_all[1, 0]*y + (w_10_all-w_30_all)
plt.figure()
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('When their covs is equal')
plt.contour(x, y, g12, 0, colors='black')
plt.contour(x, y, g23, 0, colors='red')
plt.contour(x, y, g13, 0, colors='blue')
plt.show()'''
 

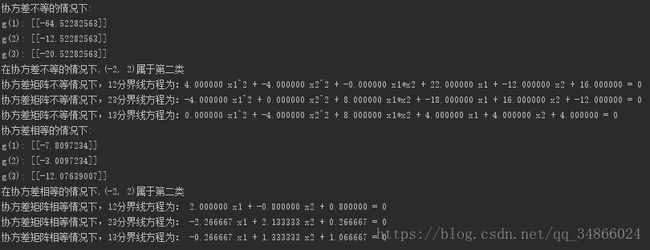
结果：嘤嘤嘤，唉，都是为了下一届学弟学妹啊~~~

运行图：

 

 

 

 

 

 

 

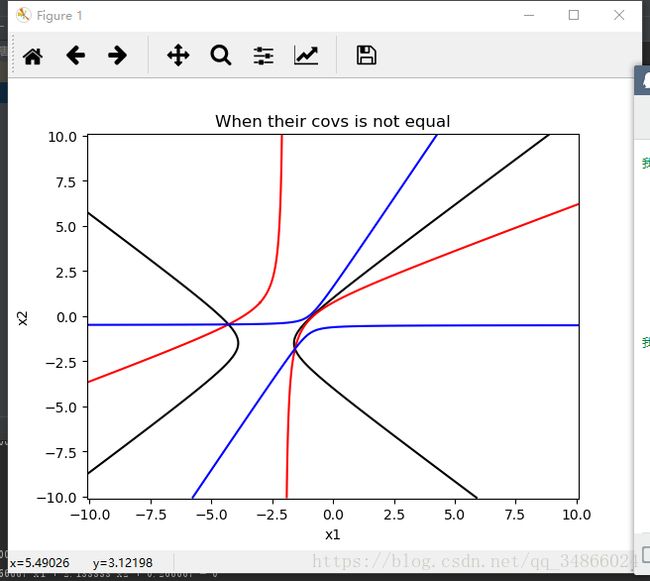
协方差不等的情况：

 

 

 

 

 

 

 

 

 

 

 

 

 

 

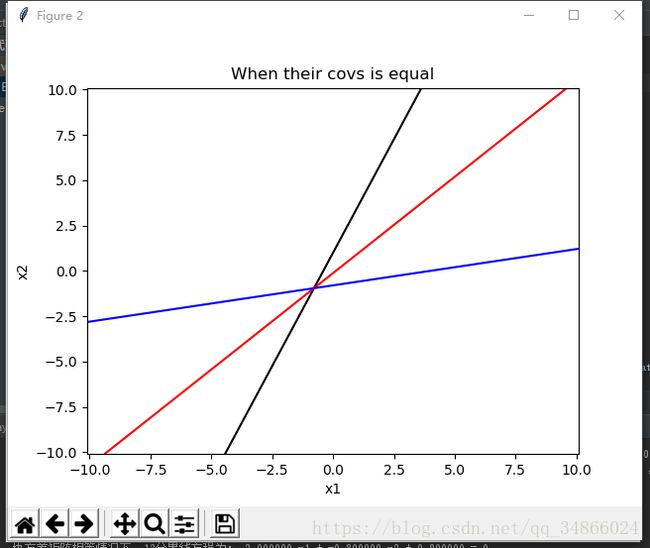
协方差相等的情况：