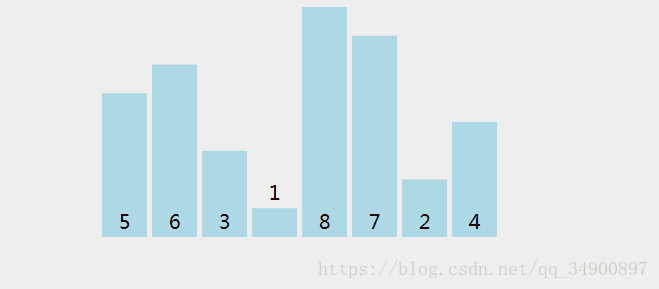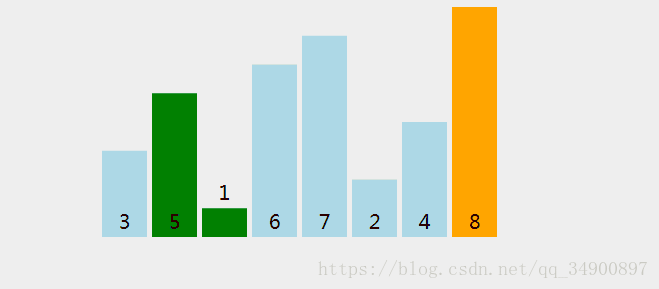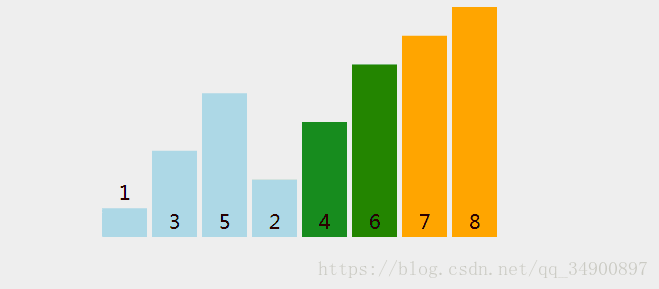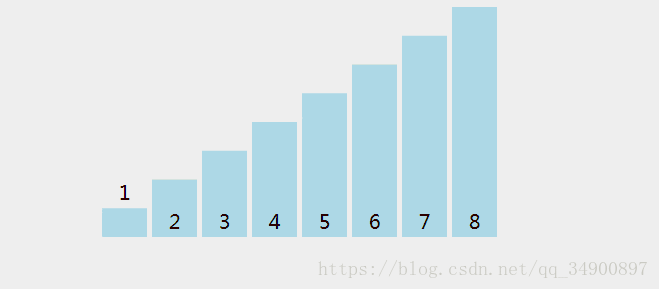kotlin 基本排序算法(冒泡、快排、二分....)与java对比
先还是把这个大神的引用地址贴上,要用到图片 搞懂基本排序算法
基本算法不管是哪种程序都会涉及,只是android用的比较少,很容易忘记,所以能掌握几种是几种吧!然而java和kotlin的写法稍微有点出入。
先来看图:
懂得理论的话,仔细看还是能看的明白的
1.第一个与第二个比较,那个大就排着后面,或者小就往后排。
2.看上面的解释是当第一次比较完后,最后的一个是里面最大的,这里思维还是有点难理解,但是多想几次就能明白,比如:第一和第二个比较,第一个大,肯定互换位置到变成第二个,然后第二个与第三个比较,如果还是第二大,互换位置,加入第二个是里面数据最大的,肯定会被换都最后一个位置直到没有,所以最后一个最大了。
3.每次排序最后一个最大所以就不用比了,直到没有比的为止。
冒泡java写法;
/**
* @param arr 待排序数组
* @param n 数组长度 arr.length
*/
private static void BubbleSort(int[] arr, int n) {
for (int i = 0; i < n - 1; i++) {
for (int j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
//交换两个元素
int temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
}
}
}
}现在已经是用kotlin写了,然后写的时候有点犯糊涂,不知道怎么写了,有点尴尬了,还是只有百度,没想到还真有,随便附上
也测试过了,然后kotlin的写法更加简单,容易比较理解,个人觉得比java写法理解起来容易
fun bub(arr:IntArray){
var out = 0
var inIndex = 0
var temp = 0
while (out < arr.size){
inIndex = out +1
while (inIndex < arr.size){
if (arr[out] > arr[inIndex]){
temp = arr[out]
arr[out] = arr[inIndex]
arr[inIndex] = temp
}
inIndex++
}
out++
}
}后面的直接上代码了,我也没有弄得好懂,如果要看解释,就看上面的那个网址
这里讲了快排分几种,单路、双路、三路
单路
private static void quickSort(int[] arr, int l, int r) {
if (l >= r) {
return;
}
// p 为 第一次 排序完成后 v 应该在的位置,即分治的划分点
int p = partition(arr, l, r);
quickSort(arr, l, p - 1);
quickSort(arr, p + 1, r);
}
private static int partition(Integer[] arr, int l, int r) {
// 为了提高效率,减少造成快速排序的递归树不均匀的概率,
// 对于一个数组,每次随机选择的数为当前 partition 操作中最小最大元素的可能性为 1/n
int randomNum = (int) (Math.random() * (r - l + 1) + l);
swap(arr, l, randomNum);
int v = arr[l];
int j = l;
for (int i = l + 1; i <= r; i++) {
if (arr[i] < v) {
swap(arr, j + 1, i);
j++;
}
}
swap(arr, l, j);
return j;
}
private static void swap( int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}双路
private static void quickSort(int[] arr, int l, int r) {
if (l >= r) {
return;
}
// 这里 p 为 小于 v 的最后一个元素,=v 的第一个元素
int p = partition(arr, l, r);
quickSort(arr, l, p - 1);
quickSort(arr, p + 1, r);
}
private static int partition(int[] arr, int l, int r) {
// 为了提高效率,减少造成快速排序的递归树不均匀的概率,
// 对于一个数组,每次随机选择的数为当前 partition 操作中最小最大元素的可能性降低
int randomNum = (int) (Math.random() * (r - l + 1) + l);
swap(arr, l, randomNum);
int v = arr[l];
int i = l + 1;
int j = r;
while (true) {
while (i <= r && arr[i] <= v) i++;
while (j >= l + 1 && arr[j] >= v) j--;
if (i > j) break;
swap(arr, i, j);
i++;
j--;
}
//j 最后角标停留在 i > j 即为 比 v 小的最后一个一元素位置
swap(arr, l, j);
return j;
}三路
private static void quickSort3(int[] num, int length) {
quickSort(num, 0, length - 1);
}
private static void quickSort(int[] arr, int l, int r) {
if (l >= r) {
return;
}
// 为了提高效率,减少造成快速排序的递归树不均匀的概率,
// 对于一个数组,每次随机选择的数为当前 partition 操作中最小最大元素的可能性 降低 1/n!
int randomNum = (int) (Math.random() * (r - l + 1) + l);
swap(arr, l, randomNum);
int v = arr[l];
// 三路快速排序即把数组划分为大于 小于 等于 三部分
//arr[l+1...lt] v 三部分
// 定义初始值得时候依旧可以保证这初始的时候这三部分都为空
int lt = l;
int gt = r;
int i = l + 1;
while (i < gt) {
if (arr[i] < v) {
swap(arr, i, lt + 1);
i++;
lt++;
} else if (arr[i] == v) {
i++;
} else {
swap(arr, i, gt - 1);
gt--;
//i++ 注意这里 i 不需要加1 因为这次交换后 i 的值仍不等于 v 可能小于 v 也可能等于 v 所以交换完成后 i 的角标不变
}
}
//循环结束的后 lt 所处的位置为 kotlin
private fun quickSort(arrs: IntArray, lowStart: Int, highEnd: Int) {
var low: Int = lowStart
var high: Int = highEnd
var povit: Int = arrs[low]
while (low < high) {
while (low < high && arrs[high] >= povit) {
high--
}
if (low < high) {
var temp: Int = arrs[high]
arrs[high] = arrs[low]
arrs[low] = temp
low++
}
while (low < high && arrs[low] <= povit) {
low++
}
if (low < high) {
var temp: Int = arrs[high]
arrs[high] = arrs[low]
arrs[low] = temp
high--
}
}
if (low > lowStart) quickSort(arrs, lowStart, low - 1)
if (high < highEnd) quickSort(arrs, low + 1, highEnd)
}选择排序
public static void sort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n; i++) {
int minIndex = i;
// for 循环 i 之后所有的数字 找到剩余数组中最小值得索引
for (int j = i + 1; j < n; j++) {
if (arr[j]< arr[minIndex]) {
minIndex = j;
}
}
swap(arr, i, minIndex);
}
}
/**
* 角标的形式 交换元素
*/
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}private fun selectSort(arrs: IntArray) {
var outIndex: Int = 0
var inIndex: Int = 0
var minIndex: Int = 0
while (outIndex < arrs.size - 1) {
inIndex = outIndex + 1
minIndex = outIndex
while (inIndex < arrs.size) {
if (arrs[minIndex] > arrs[inIndex]) {
minIndex = inIndex
}
inIndex++
}
if (minIndex != outIndex) {
var temp: Int = arrs[outIndex]
arrs[outIndex] = arrs[minIndex]
arrs[minIndex] = temp
}
outIndex++
}
}