R语言-回归分析及实现

一、数据探索阶段
1、了解变量类型
做回归分析前，了解数据集是怎样的？那些是数值型变量，那些是分类变量，这一步是相当重要的。
r代码：
> class(mydata$Middle_Price)
[1] "numeric"
> class(mydata$MPG.city.)
[1] "factor"
另外我们利用factor函数对各水平进行赋值：
status<-factor(status,order=TRUE,levels=c('poor','improved',’excellent’))
这样将1=poor 2= improved 3= excellent。
对于因子变量，利用as.numeric()将其转化为数值型。
  2、数据极端值、异常值
     大致了解变量的情况，检验有没有极端值。对于极端值，若发现特别离谱，则可以考虑删除，否则需结合业务而定。极端值在回归的时候会对回归影响很大，所以需提前查看。
> summary(mydata$Middle_Price)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
  13990   23700   32500   37560   43290  145800
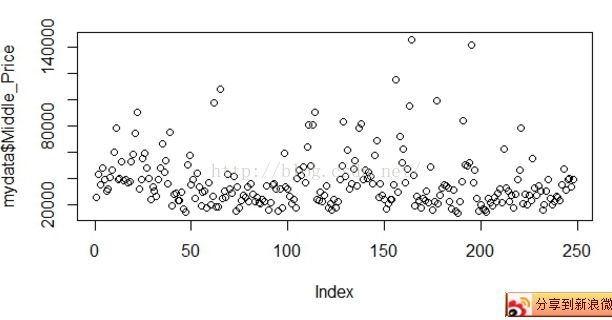
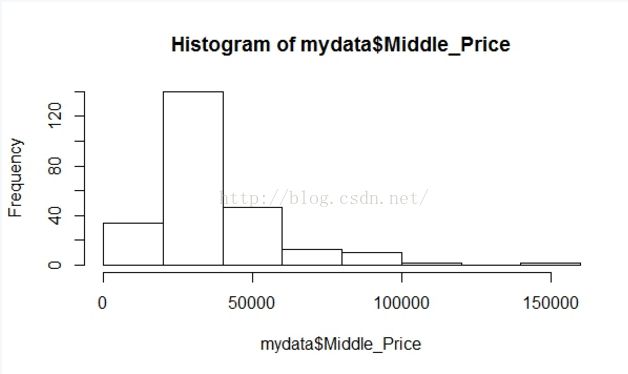
另外我们可以画图(散点图、直方图等等)查看：
plot(mydata$Middle_Price)

hist(mydata$Middle_Price)

对于分类型数据，我们也可以查看其中是否有异常值，并了解其中的分布情况
> table(mydata$cvt)
 
  0   1
211  37
 3、缺失值
由于此次试验的数据中不包含有缺失值，所以在此不多做介绍。对于缺失值，可以考虑删除样本，或者根据业务的情况进行填充等等。
 
4、数据清洗
对于发现的异常值进行处理，对缺失值进行操作，另外根据业务需求在选择部分子集进行分析等等。
 
 
二、数据描述
1、  单变量统计量
对于上面分析的变量Middle_Price，根据业务需求提出价格高于80000的样本。对于之后的样本进行单变量统计量分析：
> summary(mydata1$Middle_Price)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
  13990   23220   31410   33850   40370   78800
抑或利用psych包计算更加多的统计量的方法：
> describe(mydata1$Middle_Price)
var   n     mean       sd  median  trimmed      mad   min   max range skew kurtosis
1   1 234 33846.43 13826.62 31412.5 32285.66 12361.18 13990 78800 64810 1.04     0.88
      se
1 903.87
 
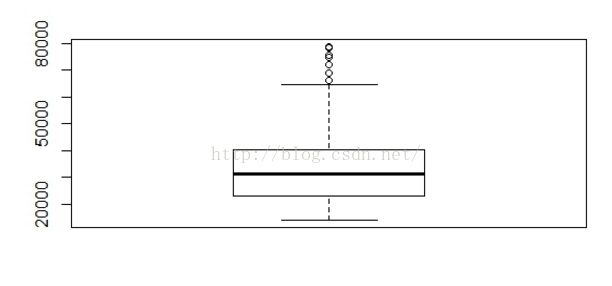
boxplot(mydata1$Middle_Price)

另外可以通过boxplot.stats查看构建图形的统计量
> boxplot.stats(mydata1$Middle_Price)
$stats
[1] 13990.0 23200.0 31412.5 40425.0 64450.0
 
$n
[1] 234
 
$conf
[1] 29633.37 33191.63
 
$out
[1] 78800 74900 66295 75600 78290 68800 72100 78555
箱式图中两条须极限不会超过盒式各段加1.5倍四分位剧的范围，此处箱式图显示出可能是离群点的几个值了。
2、  变量值的分布及其检验
对变量进行正态性检验：
> shapiro.test(mydata1$Middle_Price)
 
      Shapiro-Wilk normality test
 
data:  mydata1$Middle_Price
W = 0.9224, p-value = 9.969e-10
所以我们可以拒绝原假设，即该数据不符合正态分布变量的
3、  列联表及其表格中的统计量计算
对于衡量两个名义变量的关联性，可以采用皮尔逊卡方检验：
 
> mytable<-xtabs(~X6over+SUV,data=mydata1)
> chisq.test(mytable)
 
      Pearson's Chi-squared test with Yates' continuity correction
 
data:  mytable
X-squared = 0.0562, df = 1, p-value = 0.8127
由于p值大于0.1，可以认为X6over与SUV两个变量独立。
> mytable<-xtabs(~X6over+Sports,data=mydata1)
> chisq.test(mytable)
 
      Pearson's Chi-squared test with Yates' continuity correction
 
data:  mytable
X-squared = 7.3154, df = 1, p-value = 0.006837
由于p值小于0.1，可以认为X6over与Sports两个变量不独立。
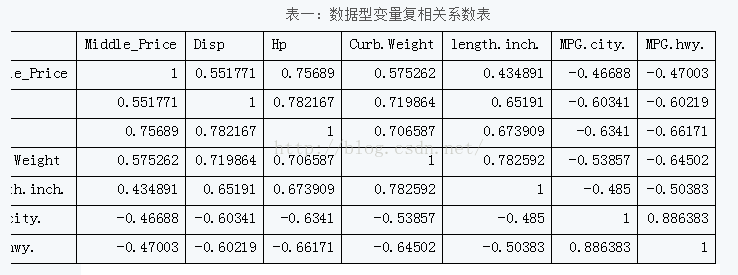
4、变量间的相关性和关联指标计算
（1）对于两个连续性变量，我们可以使用pearson相关系数和spearman相关系数进行分析。
>corr.test(mydata1$Middle_Price,mydata1$Curb.Weight,method='pearson')
Call:corr.test(x = mydata1$Middle_Price, y = mydata1$Curb.Weight,
    method = "pearson")
Correlation matrix
[1] 0.58
Sample Size
     [,1]
[1,]  234
Probability values  adjusted for multiple tests.
     [,1]
[1,]    0
> corr.test(mydata1$Middle_Price,mydata1$Curb.Weight,method='spearman')
Call:corr.test(x = mydata1$Middle_Price, y = mydata1$Curb.Weight,
    method = "spearman")
Correlation matrix
[1] 0.71
Sample Size
     [,1]
[1,]  234
Probability values  adjusted for multiple tests.
     [,1]
[1,]    0
关于两种检验的方法区别，可见：http://blog.sina.com.cn/s/blog_548d137e0101874n.html
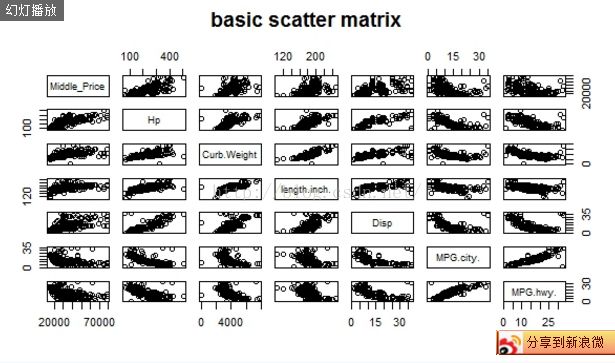
另外对于多个连续性变量，利用r散点图以及散点图矩阵进行可视化。
R语言实战中介绍了四种方法画散点矩阵。基础的散点矩阵图可用plot（）或者pairs（）函数创建。
y<-cor(newdata)
>plot(~Middle_Price+Hp+Curb.Weight+length.inch.+Disp+MPG.city.+MPG.hwy.,
+      data=mydata1,main='basic scatter matrix')
亦可以通过scatterplotmatrix（）、cpairs（）函数创建。他们可以设置平滑曲线、密度图、直方图、相关系数的颜色等等了。

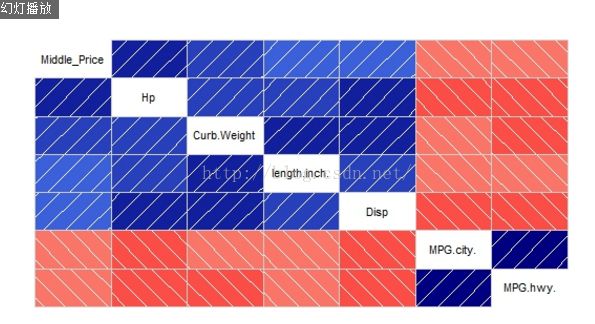
可以用corrgram包画出变量之间的相关性图，颜色越深表示变量间相关性越高。具体设置可以见help文档。蓝色和从左下指向右上的线条表示正相关，而红色和从左上指向右下的线条表示负相关。
>y<-c('Middle_Price','Hp','Curb.Weight','length.inch.','Disp','MPG.city.','MPG.hwy.')
> data<-mydata1[y]
> library(corrgram)
> corrgram(data)

（2）连续型变量和分类变量之间的相关性
其实这就是方差分析，利用F检验验证。
> aov1<-aov(Middle_Price~X6over,data=mydata1)
> summary(aov1)
             Df    Sum Sq   Mean Sq F value   Pr(>F)   
X6over        1 4.797e+09 4.797e+09      28 2.81e-07 ***
Residuals   232 3.975e+10 1.713e+08                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
P值<0.05说明小于明显具有差异，或者说Middle_Price受到X6over影响，他们之间是有相关性的。

利用names（）函数查看数据框里面的变量名，本次回归分析的数据为汽车数据，变量有：
[1] "Model"          "Middle_Price"   "X4spd"          "X6over"       
 [5] "cvt"            "Disp"           "Hp"             "AWD"          
 [9] "X4WD_dummy"     "rear"           "SUV"            "Pickup"       
[13] "Minivan"        "Sports"         "Curb.Weight"    "length.inch." 
[17] "MPG.city."      "MPG.hwy."       "Reliability"    "Electric"     
[21] "Hybrid"         "Hybrid.option."
在总共的22个变量中，Middle_Price、HP、Disp、Curb Weight、Length、MPG（city）、MPG（hwy）是数值型数据，而其余变量均是分类型变量。
根据回归分析以及r语言实现（一）介绍的方法，对其中的数据进行分析。通过之前介绍的方法，我们删除了变量Pickup、Minivan、Sports、MPG.city.、Reliability、Electric、Hybrid。
利用剩余的变量做回归：
> reg1<-lm(Middle_Price~X4spd+X6over+cvt+Disp+Hp+AWD+X4WD_dummy+rear+SUV+Curb.Weight
+           +length.inch.+MPG.hwy.+Hybrid.option.,data=mydata1)
> summary(reg1)
 
Call:
lm(formula = Middle_Price ~ X4spd + X6over + cvt + Disp + Hp +
    AWD + X4WD_dummy + rear + SUV + Curb.Weight + length.inch. +
    MPG.hwy. + Hybrid.option., data = mydata1)
 
Residuals:
   Min     1Q Median     3Q    Max
-25013  -4390   -404   2866  32870
 
Coefficients:
                Estimate  Std. Error    t value    Pr(>|t|)   
(Intercept)    27127.454   9730.687   2.788    0.00577 **
X4spd             13.530   3850.763   0.004   0.99720   
X6over          2061.117   1785.648   1.154   0.24964    
cvt             2031.623   2161.344   0.940   0.34826   
Disp             -11.100    143.297  -0.077    0.93833   
Hp               116.464     14.395   8.091   3.99e-14 ***
AWD            5306.209   1718.148   3.088   0.00227 **
X4WD_dummy     -243.168   2764.303  -0.088  0.92998   
rear            3566.848   2565.544   1.390   0.16585   
SUV            -2684.811   1792.806  -1.498   0.13568   
Curb.Weight        5.702      1.273   4.479   1.20e-05 ***
length.inch.    -263.388     64.067  -4.111    5.56e-05 ***
MPG.hwy.         162.675    136.525   1.192  0.23473   
Hybrid.option.  5902.344   2048.858   2.881  0.00436 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 8285 on 220 degrees of freedom
Multiple R-squared:  0.661,  Adjusted R-squared:  0.641
F-statistic:    33 on 13 and 220 DF,  p-value: < 2.2e-16
显然此处有部分变量没通过t检验， 将p值放宽为0.15，Hp、AWD、SUV、Curb.Weight、length.inch.、Hybrid.option.变量给予保留，在此进行全子集回归。
library(leaps)
 
reg2<-regsubsets(Middle_Price~Hp+AWD+SUV+Curb.Weight+length.inch.+Hybrid.option.,
         data=mydata1,nbest=6)
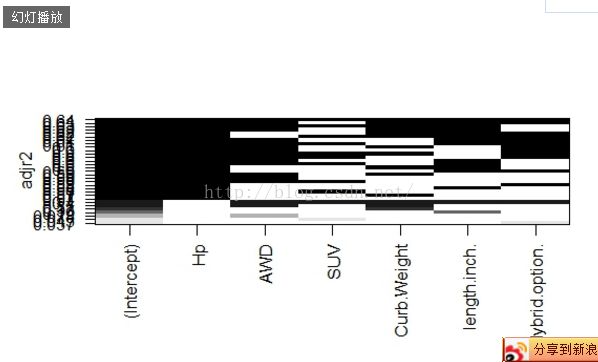
plot(reg2,scale='adjr2')

根据此图，我们可以发现6个变量均在的时候，调整r平方最大。
> reg2<-lm(Middle_Price~Hp+AWD+SUV+Curb.Weight+length.inch.+Hybrid.option.,
+          data=mydata1)
> summary(reg2)
 
Call:
lm(formula = Middle_Price ~ Hp + AWD + SUV + Curb.Weight + length.inch. +
    Hybrid.option., data = mydata1)
 
Residuals:
   Min     1Q Median     3Q    Max
-24690  -4420   -733   2958  33023
 
Coefficients:
                Estimate Std. Error t value     Pr(>|t|)   
(Intercept)    37948.658   7647.659   4.962    1.37e-06 ***
Hp               119.852      9.758  12.282  < 2e-16 ***
AWD            5175.296   1257.876   4.114  5.43e-05 ***
SUV            -3791.008   1608.088  -2.357   0.01925 * 
Curb.Weight        5.188      1.178   4.406   1.63e-05 ***
length.inch.     -290.762     57.910  -5.021    1.04e-06 ***
Hybrid.option.   6044.126   2019.045   2.994     0.00306 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 8290 on 227 degrees of freedom
Multiple R-squared:  0.6498,         Adjusted R-squared:  0.6405
F-statistic: 70.19 on 6 and 227 DF,  p-value: < 2.2e-16
此时模型整体的F检验，变量T检验全部通过。
> vif(reg2)
      Hp      AWD            SUV    Curb.Weight   length.inch.
  2.218033   1.338914    1.992868     4.806861  3.519296
Hybrid.option.
      1.035540
变量间共线性情况不严重。
接着考虑回归的残差分析，包括残差正态性检验、独立性检验、异方差检验。
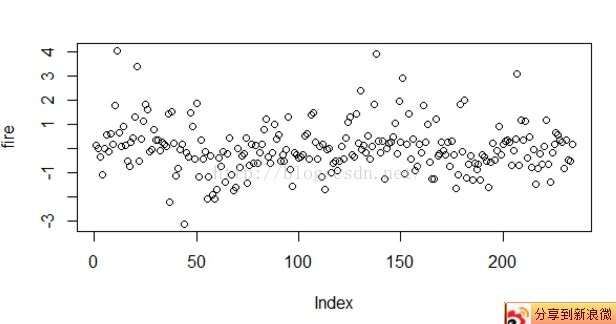
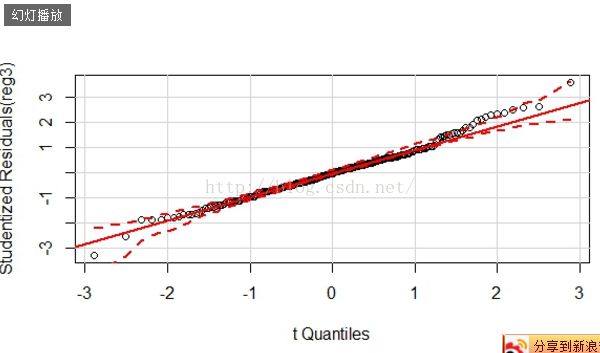
学生化残差图：

对残差进行正态性检验：
> shapiro.test(z)
 
      Shapiro-Wilk normality test
 
data:  z
W = 0.9884, p-value = 0.05514


正态性检验没有通过.


qqPlot(reg3)

根据残差图，我们得到残差有异方差性。
> ncvTest(reg3)
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 47.6273    Df = 1     p = 5.154573e-12
由于p值明显小于0.1，所以存在严重的异方差性。
对于方差独立性检验：
> durbinWatsonTest(reg3)
lag Autocorrelation D-W Statistic p-value
   1       0.2623158      1.473875       0
Alternative hypothesis: rho != 0
由于p值明显小于0.1，所以存在严重的相关性。
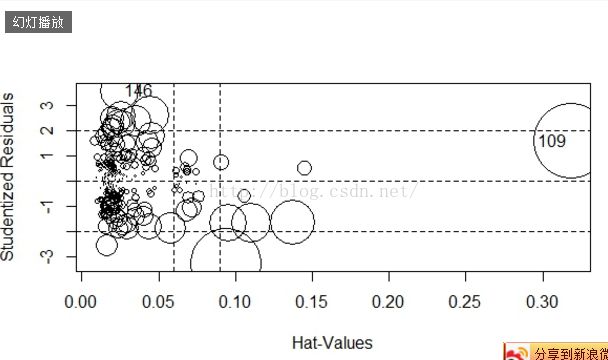
强影响点分析：
另外对其强影响点、高杠杆点以及离群点作图。

     StudRes        Hat     CookD
109 1.609110 0.31863100 0.4144524
146 3.609866 0.02444116 0.2104563
检查提示的数据样本，看是否是因为输入错误问题。如果是输入错误，可以考虑删除样本。如果不是，则根据实际情况进行处理。