想玩下ShaderToy,但是突然想起来自己以前用Bitmap实现的分形图形，
那么用Shader实现起来又是如何呢。
1.曼德博罗集
分形几何是什么呢，似乎不是本文的主题，我这里有一系列的链接
《走近混沌》-1-从分形龙谈起
《走近混沌》-2-简单分形
《走近混沌》-3-分数维是怎么回事？
《走近混沌》-4-再回到分形龙
《走近混沌》-5-大自然中的分形
《走近混沌》-6-分形之父的启示
《走近混沌》-7-魔鬼的聚合物-曼德勃罗集
《走近混沌》-8-朱利亚的故事
我在这里仅仅贴出部分，更广阔的数学殿堂等你开拓
言归正传，分形几何的奇妙图案，只由一个简单的迭代式子决定，我反正惊呆了
[图片上传失败...(image-b91ac5-1512724032048)]
观察上述式子，如果对复数稍有了解，应该知道这个式子表明(n+1)项的数值是在第(n)的基础之上迭代而来,可能有点难以理解
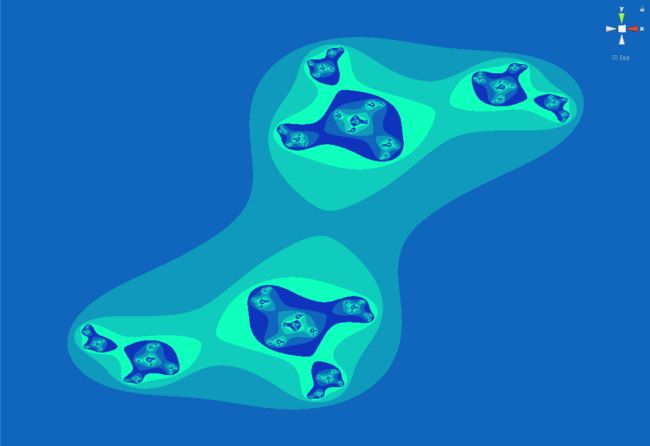
先上一张效果图
QQ图片20170830143252.png
上图中淡青色区域，表示经过无限次迭代之后z(n)的模的大小依旧限定在某一区域不会跑偏（发散）到无穷远处，我们在对无穷次迭代之后会发散的这些位置点涂上不同的颜色，而具体上什么颜色，是由发散的次数不同来决定的
不多说，上代码
Shader "shadertoy/Simple Circle" {
Properties{
iMouse("Mouse Pos", Vector) = (100, 100, 0, 0)
_Parameters("Circle Parameters", Vector) = (0.5, 0.5, 10, 1) // Center: (x, y), Radius: z
_CircleColor("Circle Color", Color) = (1, 1, 1, 1)
_BackgroundColor("Background Color", Color) = (1, 1, 1, 1)
}
CGINCLUDE
#include "UnityCG.cginc"
#pragma target 3.0
#define vec2 float2
#define vec3 float3
#define vec4 float4
#define mat2 float2x2
#define mod fmod
#define mix lerp
#define atan atan2
#define fract frac
#define texture2D tex2D
// 屏幕的尺寸
#define iResolution _ScreenParams
// 屏幕中的坐标，以pixel为单位
#define gl_FragCoord ((_iParam.srcPos.xy/_iParam.srcPos.w)*_ScreenParams.xy)
#define PI2 6.28318530718
#define pi 3.14159265358979
#define halfpi (pi * 0.5)
#define oneoverpi (1.0 / pi)
#define CycleCount 100
#define iGlobalTime _Time.y
float4 _Parameters;
float4 _CircleColor;
float4 _BackgroundColor;
fixed4 iMouse;
uniform float theta;
struct v2f {
float4 pos : SV_POSITION;
float4 srcPos : TEXCOORD0;
};
struct Complex {//z = ai + b;
float a;
float b;
};
// precision highp float;
v2f vert(appdata_base v) {//顶点着色器
v2f o;
o.pos = mul(UNITY_MATRIX_MVP, v.vertex);
o.srcPos = ComputeScreenPos(o.pos);
return o;
}
vec4 main(vec2 fragCoord);
fixed4 frag(v2f _iParam) : COLOR0{//片元着色器
vec2 fragCoord = gl_FragCoord;
return main(gl_FragCoord);
}
float calManDeBoLuo(Complex c, int cycleIndex, float sin, float cos ) {
Complex z;
z.a = sin;
z.b = cos;
z.a = 0;
z.b = 0;
float magnite;
do {
cycleIndex++;
float aa = 2 * z.a * z.b + c.a;
float bb = pow(z.b, 2) - pow(z.a, 2) + c.b;
z.a = aa;
z.b = bb;
magnite = length(float2(z.a, z.b));
if (cycleIndex >= CycleCount || magnite > 2) {
return cycleIndex*1.0 / CycleCount;
}
} while (true);
}
float calJulia(Complex z, int cycleIndex, float sin, float cos) {
Complex c;
c.a = sin;
c.b = cos;
float magnite;
do {
cycleIndex++;
float aa = 2 * z.a * z.b + c.a;
float bb = pow(z.b, 2) - pow(z.a, 2) + c.b;
z.a = aa;
z.b = bb;
magnite = length(float2(z.a, z.b));
if (cycleIndex >= CycleCount || magnite > 2) {
return cycleIndex*1.0 / CycleCount;
}
} while (true);
}
vec4 main(vec2 fragCoord) {//主函数
vec2 pos = fragCoord; // pos.x ~ (0, iResolution.x), pos.y ~ (0, iResolution.y)
float2 viewPortCoor = float2( fragCoord.x/ iResolution.x, fragCoord.y/ iResolution.y);// (0,0) - (1,1) 中心位置为(0.5,0.5)
float scale =1/ (1 + -0.5 * (sin(_Time.y)*0.5 + 0.5));//
//viewPortCoor = (scale) * (viewPortCoor * 2 * 1 - float2(1, 1)) - float2(-0.33,0.04752) ;//(-1,-1) - (1,1) 中心位置为(0,0)
viewPortCoor = scale * (viewPortCoor * 2 * 1 - float2(1, 1)) ;//(-1,-1) - (1,1) 中心位置为(0,0)
Complex vpc;
vpc.a = viewPortCoor.y ;
vpc.b = viewPortCoor.x ;
float cal = calManDeBoLuo(vpc, 0, sin(_Time.y), cos(_Time.y));//曼德博罗集
//float cal = calJulia(vpc, 0, sin(_Time.y/3) , cos(_Time.y / 3) );//茱莉亚集
return float4(0, cal, 0, 1);
}
ENDCG
SubShader{
Pass{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#pragma fragmentoption ARB_precision_hint_fastest
ENDCG
}
}
FallBack Off
}
2.茱莉亚集
看代码的这个部分
float cal = calManDeBoLuo(vpc, 0, sin(_Time.y), cos(_Time.y));//曼德博罗集
//float cal = calJulia(vpc, 0, sin(_Time.y/3) , cos(_Time.y / 3) );//茱莉亚集
我们把茱莉亚集的代码打开，同时把曼德博罗集的代码注释掉
像这样
//float cal = calManDeBoLuo(vpc, 0, sin(_Time.y), cos(_Time.y));//曼德博罗集
float cal = calJulia(vpc, 0, sin(_Time.y/3) , cos(_Time.y / 3) );//茱莉亚集
你可以在unity中看到绕中心旋转的一个茱莉亚集
QQ截图20170830144906.png
我承认为了好看加上了时间函数 。
3.效果调整
上图的颜色因为受迭代次数的影响很不均匀，同时颜色较为单一，为了解决这个美学问题（存粹强迫症）
我们对返回颜色值的部分做一些插值变换
float colorTime1 = cos(_Time.y)*0.5 + 0.5;
float colorTime2 = sin(_Time.y)*0.5 + 0.5;
float4 color = float4(colorTime1, cal*20.0%1.0, colorTime2, 1);
我们这里简单截几张效果图
QQ截图20170831133457.png
QQ截图20170831133508.png
QQ截图20170831133441.png
完整代码如下
Shader "shadertoy/Simple Circle" {
Properties{
iMouse("Mouse Pos", Vector) = (100, 100, 0, 0)
_Parameters("Circle Parameters", Vector) = (0.5, 0.5, 10, 1) // Center: (x, y), Radius: z
_CircleColor("Circle Color", Color) = (1, 1, 1, 1)
_BackgroundColor("Background Color", Color) = (1, 1, 1, 1)
}
CGINCLUDE
#include "UnityCG.cginc"
#pragma target 3.0
#define vec2 float2
#define vec3 float3
#define vec4 float4
#define mat2 float2x2
#define mod fmod
#define mix lerp
#define atan atan2
#define fract frac
#define texture2D tex2D
// 屏幕的尺寸
#define iResolution _ScreenParams
// 屏幕中的坐标，以pixel为单位
#define gl_FragCoord ((_iParam.srcPos.xy/_iParam.srcPos.w)*_ScreenParams.xy)
#define PI2 6.28318530718
#define pi 3.14159265358979
#define halfpi (pi * 0.5)
#define oneoverpi (1.0 / pi)
#define CycleCount 100
#define iGlobalTime _Time.y
float4 _Parameters;
float4 _CircleColor;
float4 _BackgroundColor;
fixed4 iMouse;
uniform float theta;
struct v2f {
float4 pos : SV_POSITION;
float4 srcPos : TEXCOORD0;
};
struct Complex {//z = ai + b;
float a;
float b;
};
// precision highp float;
v2f vert(appdata_base v) {//顶点着色器
v2f o;
o.pos = mul(UNITY_MATRIX_MVP, v.vertex);
o.srcPos = ComputeScreenPos(o.pos);
return o;
}
vec4 main(vec2 fragCoord);
fixed4 frag(v2f _iParam) : COLOR0{//片元着色器
vec2 fragCoord = gl_FragCoord;
return main(gl_FragCoord);
}
float calManDeBoLuo(Complex c, int cycleIndex, float sin, float cos ) {
Complex z;
z.a = sin;
z.b = cos;
z.a = 0;
z.b = 0;
float magnite;
do {
cycleIndex++;
float aa = 2 * z.a * z.b + c.a;
float bb = pow(z.b, 2) - pow(z.a, 2) + c.b;
z.a = aa;
z.b = bb;
magnite = length(float2(z.a, z.b));
if (cycleIndex >= CycleCount || magnite > 2) {
return cycleIndex*1.0 / CycleCount;
}
} while (true);
}
float calJulia(Complex z, int cycleIndex, float sin, float cos) {
Complex c;
c.a = sin;
c.b = cos;
float magnite;
do {
cycleIndex++;
float aa = 2 * z.a * z.b + c.a;
float bb = pow(z.b, 2) - pow(z.a, 2) + c.b;
z.a = aa;
z.b = bb;
magnite = length(float2(z.a, z.b));
if (cycleIndex >= CycleCount || magnite > 2) {
return cycleIndex*1.0 / CycleCount;
}
} while (true);
}
vec4 main(vec2 fragCoord) {//主函数
vec2 pos = fragCoord; // pos.x ~ (0, iResolution.x), pos.y ~ (0, iResolution.y)
float2 viewPortCoor = float2( fragCoord.x/ iResolution.x, fragCoord.y/ iResolution.y);// (0,0) - (1,1) 中心位置为(0.5,0.5)
float scale =1/ (1 + -0.5 * (sin(_Time.y)*0.5 + 0.5));//
//viewPortCoor = (scale) * (viewPortCoor * 2 * 1 - float2(1, 1)) - float2(-0.33,0.04752) ;//(-1,-1) - (1,1) 中心位置为(0,0)
viewPortCoor = scale * (viewPortCoor * 2 * 1 - float2(1, 1)) ;//(-1,-1) - (1,1) 中心位置为(0,0)
Complex vpc;
vpc.a = viewPortCoor.y ;
vpc.b = viewPortCoor.x ;
//float cal = calManDeBoLuo(vpc, 0, sin(_Time.y), cos(_Time.y));//曼德博罗集
float cal = calJulia(vpc, 0, sin(_Time.y/3) , cos(_Time.y / 3) );//茱莉亚集
float colorTime1 = cos(_Time.y)*0.5 + 0.5;
float colorTime2 = sin(_Time.y)*0.5 + 0.5;
float4 color = float4(colorTime1, cal*20.0%1.0, colorTime2, 1);
return color;
}
ENDCG
SubShader{
Pass{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#pragma fragmentoption ARB_precision_hint_fastest
ENDCG
}
}
FallBack Off
}
再贴几张
QQ截图20170831135700.png
QQ截图20170831135357.png
Have Fun !