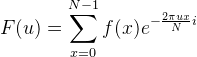傅里叶变换 二维快速傅里叶变换(快速的二维离散傅里叶变换、分治法)
1、一维FFT和二维FFT。
一维DFT公式:
二维DFT公式:
可以看作M行N列的二维数组,先对每行做一维FFT,将结果作为一个新的二维数组。再对新的二维数组每列做一维FFT。而在处理二维IFFT的时候,跟二维FFT差不多,只要在公共方法中控制正负值,来区分是FFT还是IFFT。如果是FFT的话,刚开始的时候,要将double转为Complex复数,如果是IFFT的话,要在结束的时候,将每个值都除以MN。可以模仿文章一维快速傅里叶变换、二维离散傅里叶变换(代码和性能的优化)的写法,相结合的话,就可以很容易得出二维FFT的写法。
2、复数类。
package com.zxj.reptile.utils.number;
public class Complex {
private double real;//实数
private double image;//虚数
public Complex() {
real = 0;
image = 0;
}
public Complex(double real) {
this.real = real;
this.image = 0;
}
public Complex(double real, double image) {
this.real = real;
this.image = image;
}
//加:(a+bi)+(c+di)=(a+c)+(b+d)i
public Complex add(Complex complex) {
double real = complex.getReal();
double image = complex.getImage();
double newReal = this.real + real;
double newImage = this.image + image;
return new Complex(newReal, newImage);
}
//减:(a+bi)-(c+di)=(a-c)+(b-d)i
public Complex sub(Complex complex) {
double real = complex.getReal();
double image = complex.getImage();
double newReal = this.real - real;
double newImage = this.image - image;
return new Complex(newReal, newImage);
}
//乘:(a+bi)(c+di)=(ac-bd)+(bc+ad)i
public Complex mul(Complex complex) {
double real = complex.getReal();
double image = complex.getImage();
double newReal = this.real * real - this.image * image;
double newImage = this.image * real + this.real * image;
return new Complex(newReal, newImage);
}
//乘:a(c+di)=ac+adi
public Complex mul(double multiplier) {
return mul(new Complex(multiplier));
}
//除:(a+bi)/(c+di)=(ac+bd)/(c^2+d^2) +((bc-ad)/(c^2+d^2))i
public Complex div(Complex complex) {
double real = complex.getReal();
double image = complex.getImage();
double denominator = real * real + image * image;
double newReal = (this.real * real + this.image * image) / denominator;
double newImage = (this.image * real - this.real * image) / denominator;
return new Complex(newReal, newImage);
}
public double getReal() {
return real;
}
public void setReal(double real) {
this.real = real;
}
public double getImage() {
return image;
}
public void setImage(double image) {
this.image = image;
}
@Override
public String toString() {
String str = "";
if (real != 0) {
str += real;
} else {
str += "0";
}
if (image < 0) {
str += image + "i";
} else if (image > 0) {
str += "+" + image + "i";
}
return str;
}
//欧拉公式 e^(ix)=cosx+isinx
public static Complex euler(double x) {
double newReal = Math.cos(x);
double newImage = Math.sin(x);
return new Complex(newReal, newImage);
}
/**
* 比较两个复数是否相等,并可以调节小数精度误差
*
* @param a 复数a
* @param b 复数b
*/
public static boolean equals(Complex a, Complex b) {
return NumberUtils.getRound(a.getImage(), 4) == NumberUtils.getRound(b.getImage(), 4) &&
NumberUtils.getRound(a.getReal(), 4) == NumberUtils.getRound(b.getReal(), 4);
}
/**
* 比较两个复数数组是否相等,小数精度误差在6位数
*
* @param a 复数数组a
* @param b 复数数组b
*/
public static boolean equals(Complex[] a, Complex[] b) {
if (a.length != b.length) {
return false;
}
for (int i = 0; i < a.length; i++) {
if (!equals(a[i], b[i])) {
return false;
}
}
return true;
}
/**
* 比较两个二维复数数组是否相等,小数精度误差在6位数
*
* @param a 二维复数数组a
* @param b 二维复数数组b
*/
public static boolean equals(Complex[][] a, Complex[][] b) {
if (a.length != b.length) {
return false;
}
for (int i = 0; i < a.length; i++) {
if (!equals(a[i], b[i])) {
return false;
}
}
return true;
}
/**
* 将复数数组转换为double数组
*
* @param complexArray 复数数组
*/
public static double[] getDoubleArray(Complex[] complexArray) {
int length = complexArray.length;
double[] doubleArray = new double[length];
for (int i = 0; i < length; i++) {
doubleArray[i] = NumberUtils.getRound(complexArray[i].getReal(), 2);
}
return doubleArray;
}
/**
* 将double数组转换为复数数组
*
* @param doubleArray double数组
*/
public static Complex[] getComplexArray(double[] doubleArray) {
int length = doubleArray.length;
Complex[] complexArray = new Complex[length];
for (int i = 0; i < length; i++) {
complexArray[i] = new Complex(doubleArray[i]);
}
return complexArray;
}
/**
* 将二维double数组转换为二维复数数组
*
* @param doubleArray double二维数组
*/
public static Complex[][] getComplexArray(double[][] doubleArray) {
int length = doubleArray.length;
Complex[][] complexArray = new Complex[length][];
for (int i = 0; i < length; i++) {
complexArray[i] = getComplexArray(doubleArray[i]);
}
return complexArray;
}
/**
* 二维复数数组转置
*
* @param a 二维复数数组
*/
public static Complex[][] transform(Complex[][] a) {
int row = a.length;
int column = a[0].length;
Complex[][] result = new Complex[column][row];
for (int i = 0; i < column; i++)
for (int j = 0; j < row; j++)
result[i][j] = a[j][i];
return result;
}
}
3、FourierUtils类。
package com.zxj.reptile.utils.image;
import com.zxj.reptile.utils.number.Complex;
import com.zxj.reptile.utils.number.NumberUtils;
public class FourierUtils {
/**
* 一维离散傅里叶变换DFT
*
* @param array 一维数组
*/
public static Complex[] getDft(double[] array) {
Complex[] complexArray = Complex.getComplexArray(array);
return dftProgress(complexArray, -1);
}
/**
* 一维逆离散傅里叶变换IDFT
*
* @param complexArray 一维复数数组
*/
public static double[] getInverseDft(Complex[] complexArray) {
int length = complexArray.length;
Complex[] resultArray = dftProgress(complexArray, 1);
double[] array = new double[length];
for (int i = 0; i < length; i++) {
array[i] = NumberUtils.getRound(resultArray[i].getReal() / length, 2);
}
return array;
}
/**
* 一维离散傅里叶变换DFT和一维逆离散傅里叶变换IDFT计算过程
*
* @param array 复数数组
* @param minus 正负值,DFT=-1,IDFT=1
*/
private static Complex[] dftProgress(Complex[] array, int minus) {
int length = array.length;
Complex[] complexArray = new Complex[length];
// minus * 2 * PI / N
double flag = minus * 2 * Math.PI / length;
for (int i = 0; i < length; i++) {
Complex sum = new Complex();
for (int j = 0; j < length; j++) {
//array[x] * e^((minus * 2 * PI * k / N)i)
Complex complex = Complex.euler(flag * i * j).mul(array[j]);
sum = complex.add(sum);
}
//累加
complexArray[i] = sum;
}
return complexArray;
}
/**
* 二维离散傅里叶变换DFT
*
* @param arrays 二维数组
*/
public static Complex[][] getDft(double[][] arrays) {
Complex[][] complexArrays = Complex.getComplexArray(arrays);
return dftProgress(complexArrays, -1);
}
/**
* 二维逆离散傅里叶变换IDFT
*
* @param complexArrays 二维复数数组
*/
public static double[][] getInverseDft(Complex[][] complexArrays) {
int row = complexArrays.length;
int column = complexArrays[0].length;
int size = row * column;
complexArrays = dftProgress(complexArrays, 1);
double[][] arrays = new double[row][column];
//每个数
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
arrays[i][j] = NumberUtils.getRound(complexArrays[i][j].getReal() / size, 2);
}
}
return arrays;
}
/**
* 二维离散傅里叶变换DFT和二维逆离散傅里叶变换IDFT处理过程
*
* @param complexArrays 二维复数数组
* @param minus 正负值,DFT=-1,IDFT=1
*/
private static Complex[][] dftProgress(Complex[][] complexArrays, int minus) {
int length = complexArrays.length;
//对每行进行一维DFT
for (int i = 0; i < length; i++) {
complexArrays[i] = dftProgress(complexArrays[i], minus);
}
//倒置,即行和列互换
complexArrays = Complex.transform(complexArrays);
length = complexArrays.length;
//对每行进行一维DFT,实际上是对没倒置前数组的列做一维DFT
for (int i = 0; i < length; i++) {
complexArrays[i] = dftProgress(complexArrays[i], minus);
}
//倒置回来
complexArrays = Complex.transform(complexArrays);
return complexArrays;
}
/**
* 一维快速傅里叶变换FFT 当N不是2次幂时,自动补0
*
* @param array 一维数组
*/
public static Complex[] getFft(double[] array) {
//实际的长度
int length = array.length;
//调节过的长度
int variableLength = (int) NumberUtils.getVariablePow(length, 2);
Complex[] variableArray = new Complex[variableLength];
for (int i = 0; i < variableLength; i++) {
if (i < length) {
variableArray[i] = new Complex(array[i]);
} else {
variableArray[i] = new Complex();
}
}
return fftProgress(variableArray, -1);
}
/**
* 一维逆快速傅里叶变换IFFT 将结果超过realLength的全部移除
*
* @param complexArray 一维复数数组
* @param realLength 返回的数组长度
*/
public static double[] getInverseFft(Complex[] complexArray, int realLength) {
int length = complexArray.length;
Complex[] resultArrays = fftProgress(complexArray, 1);
double[] array = new double[realLength];
//每个数都要除以N
for (int i = 0; i < realLength; i++) {
array[i] = NumberUtils.getRound(resultArrays[i].getReal() / length, 2);
}
return array;
}
/**
* 一维快速傅里叶变换FFT和一维逆快速傅里叶变换IFFT递归过程
*
* @param complexArray 一维复数数组
* @param minus FFT为1,IFFT为-1
*/
private static Complex[] fftProgress(Complex[] complexArray, int minus) {
int length = complexArray.length;
if (length == 2) {
//F(0)=f(0)+f(1),F(1)=f(0)-f(1)
return new Complex[]{
complexArray[0].add(complexArray[1]),
complexArray[0].sub(complexArray[1]),};
} else if (length == 1) {
return complexArray;
}
int middle = length / 2;
//
Complex[] a = new Complex[middle];//a(x)=f(2x)
Complex[] b = new Complex[middle];//b(x)=f(2x+1)
for (int i = 0; i < middle; i++) {
a[i] = complexArray[2 * i];
b[i] = complexArray[2 * i + 1];
}
//
Complex[] complexesA = fftProgress(a, minus);//计算G(k)
Complex[] complexesB = fftProgress(b, minus);//计算P(k)
Complex[] resultArray = new Complex[length];//F(k)
double flag = minus * 2 * Math.PI / length;//2Pi*k/N
for (int i = 0; i < middle; i++) {
//e^(2Pi*k/N)
Complex complex = Complex.euler(flag * i).mul(complexesB[i]);
//F(k)=G(k)+(e^(2Pi*k/N))*P(k)
resultArray[i] = complexesA[i].add(complex);
//F(k+(N/2))=G(k)+(e^(2Pi*(k+(N/2))/N))*P(k+(N/2))
resultArray[i + middle] = complexesA[i].sub(complex);
}
return resultArray;
}
/**
* 二维快速傅里叶变换FFT 当N不是2次幂时,自动补0
*
* @param arrays 二维数组
*/
public static Complex[][] getFft(double[][] arrays) {
//实际的行列
int row = arrays.length;
int column = arrays[0].length;
//调节过的长度
int variableLength = (int) NumberUtils.getVariablePow(row > column ? row : column, 2);
Complex[][] complexArrays = new Complex[variableLength][variableLength];
for (int i = 0; i < variableLength; i++) {
for (int j = 0; j < variableLength; j++) {
if (i < row && j < column) {
complexArrays[i][j] = new Complex(arrays[i][j]);
} else {
complexArrays[i][j] = new Complex();
}
}
}
return fftProgress(complexArrays, -1);
}
/**
* 二维逆快速傅里叶变换IFFT 将结果行列分别超过realRow和realColumn的全部移除
*
* @param complexArrays 二维复数数组
*/
public static double[][] getInverseFft(Complex[][] complexArrays, int realRow, int realColumn) {
int size = complexArrays.length * complexArrays[0].length;
complexArrays = fftProgress(complexArrays, 1);
double[][] arrays = new double[realRow][realColumn];
//每个数
for (int i = 0; i < realRow; i++) {
for (int j = 0; j < realColumn; j++) {
arrays[i][j] = NumberUtils.getRound(complexArrays[i][j].getReal() / size, 2);
}
}
return arrays;
}
/**
* 二维快速傅里叶变换DFT和二维逆快速傅里叶变换IDFT处理过程
*
* @param complexArrays 二维复数数组
* @param minus 正负值,DFT=-1,IDFT=1
*/
private static Complex[][] fftProgress(Complex[][] complexArrays, int minus) {
int length = complexArrays.length;
//对每行进行一维DFT
for (int i = 0; i < length; i++) {
complexArrays[i] = fftProgress(complexArrays[i], minus);
}
//倒置,即行和列互换
complexArrays = Complex.transform(complexArrays);
length = complexArrays.length;
//对每行进行一维DFT,实际上是对没倒置前数组的列做一维DFT
for (int i = 0; i < length; i++) {
complexArrays[i] = fftProgress(complexArrays[i], minus);
}
//倒置回来
complexArrays = Complex.transform(complexArrays);
return complexArrays;
}
}4、工具方法。
/**
* 随机生成二维数组
*
* @param row 行数
* @param column 列数
* @param minValue 最小值(包括)
* @param maxValue 最大值(包括)
*/
public static double[][] getRandom(int row, int column, int minValue, int maxValue) {
int range = maxValue - minValue + 1;
double[][] arrays = new double[row][column];
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
arrays[i][j] = (int) (Math.random() * range) + minValue;
}
}
return arrays;
}5、主流程。
public class FourierTest {
public static void main(String[] args) {
System.out.println("------开始------");
testDft(128, 128);//二维离散傅里叶变换
System.out.println("------结束------");
}
private static void testDft(int row, int column) {
long time;
System.out.println("原数据: ");
double[][] arrays = ArrayUtils.getRandom(row, column, 0, 255);
System.out.println(String.format("大小为%d行%d列", row, column));
System.out.println();
//
System.out.println("二维离散傅里叶变换DFT: ");
time = System.currentTimeMillis();
Complex[][] dftArrays = FourierUtils.getDft(arrays);
System.out.println("花费时间 :" + (System.currentTimeMillis() - time));
System.out.println();
//
System.out.println("二维逆离散傅里叶变换IDFT: ");
time = System.currentTimeMillis();
double[][] inverseDftArrays = FourierUtils.getInverseDft(dftArrays);
System.out.println("花费时间 :" + (System.currentTimeMillis() - time));
if (ArrayUtils.equals(arrays, inverseDftArrays)) {
System.out.println("DFT变换成功");
} else {
System.out.println("DFT变换失败");
}
System.out.println();
//
System.out.println("二维快速傅里叶变换FFT: ");
time = System.currentTimeMillis();
Complex[][] fftArrays = FourierUtils.getFft(arrays);
System.out.println("花费时间 :" + (System.currentTimeMillis() - time));
System.out.println();
//
System.out.println("二维逆快速傅里叶变换IFFT: ");
time = System.currentTimeMillis();
double[][] inverseFftArrays = FourierUtils.getInverseFft(fftArrays, row, column);
System.out.println("花费时间 :" + (System.currentTimeMillis() - time));
if (ArrayUtils.equals(arrays, inverseFftArrays)) {
System.out.println("FFT变换成功");
} else {
System.out.println("FFT变换失败");
}
System.out.println();
}
}6、测试结果。设置行列大小都为128的时候,发现二维DFT和二维FFT差距还是很明显的,随着行列的增大,差距只会越来越大。
7测试结果。设置行为800,列为900。行和列不仅不相等,还都不是2的幂。还要将DFT的代码注释了,不然跑不动。差不多照片的大小就怎么大了,时间花费了4s多,但是暂时还能接受吧。