堆排序的思路以及代码的实现

关于堆的一些知识点回顾

1. 堆是一个完全二叉树
2. 完全二叉树即是：若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。
3. 堆满足两个性质: 堆的每一个父节点数值都大于（或小于）其子节点，堆的每个左子树和右子树也是一个堆。
4. 堆分为最小堆和最大堆。最大堆就是每个父节点的数值要大于孩子节点，最小堆就是每个父节点的数值要小于孩子节点。排序要求从小到大的话，我们需要建立最大堆，反之建立最小堆。
5. 堆的存储一般用数组来实现。假如父节点的数组下标为i的话，那么其左右节点的下标分别为：(2*i+1)和 (2*i+2)。如果孩子节点的下标为j的话，那么其父节点的下标为(j-1)/2。
6. 完全二叉树中，假如有n个元素，那么在堆中最后一个父节点位置为(n/2-1)。

---

算法思想

1. 建立堆
2. 调整堆

3. 交换堆顶元素和堆的最后一个元素

   假如现在有一个数组a[8]={100,33,3,7,11,6,8,5};首先我们要建立完全二叉树。
   如下图所示：

然后根据各个父节点，进行一个划分。如图所示：

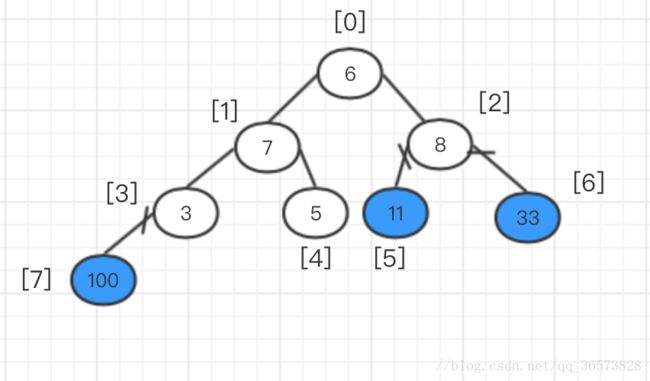
该算法的就是将各个父节点与其自己的孩子结点进行对比，然后交换的过程。根据例子，建立一个最大堆，要求每一个父节点的数值是大于孩子节点的。顺序是从最后一个父节点开始（从左至右，从下至上）。所以第一个父节点是数组下标为3的7,黄色区域中的父节点与孩子节点对比后，发现父节点已经大于孩子节点了，所以不用进行交换了。接下来的顺序就是紫色框中的二叉树，就是数组下标为2的数字3，以数字3为父节点，对比它的孩子节点，从左到右，发现右孩子的数值比父节点大，那么将右节点和父节点进行数值交换。交换后的堆如图所示：

交换结束后，再看蓝色框中的二叉树，就是以数组下标为1的数字33，以33为父节点，看它的孩子节点是否大于父节点，结果发现不大于，则不用交换。此时这个完全二叉树已经是一个堆。
接下来可以讲堆顶元素和堆的最后一个元素进行互换，然后再降最后一个元素至于完全二叉树外。

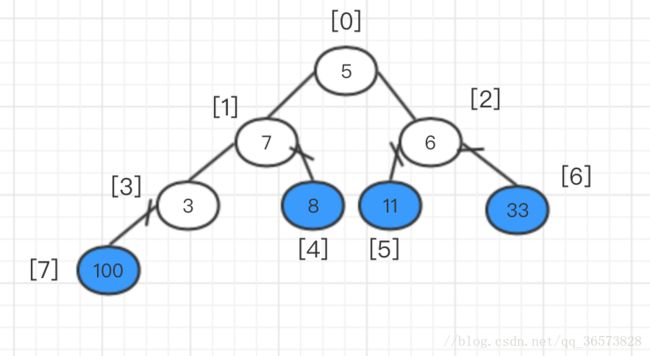
此时完全二叉树中，除去100这个元素之后，这个完全二叉树已经不满足堆的性质，所以要进行调整，此时的每次调整要从根节点（和创建堆不一样）开始进行调整，而且父节点和孩子节点交换后，要追踪到交换的孩子节点上（我用浅蓝色标志的部分）。

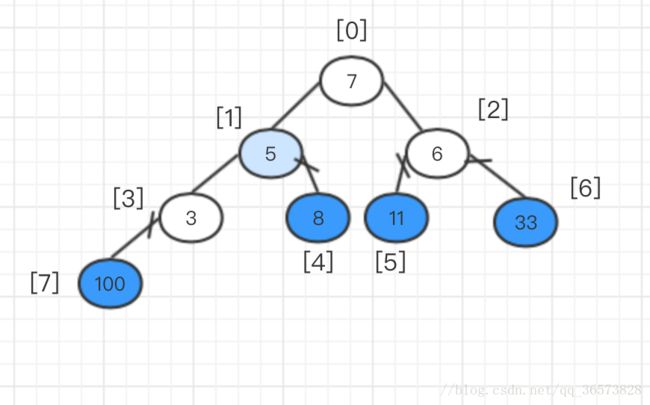
此时33和5交换了位置，那么就要从5为父节点，开始往下再和孩子节点进行比较，此时发现孩子节点和父节点中最大为11，那么将11和父节点（即数字5）互换位置。

此时堆已经调整好，再将堆顶元素和堆的最后一个元素互换，即将33和3互换，然后再降33至于完全二叉树外。

此时再进行堆的调整，从根开始。

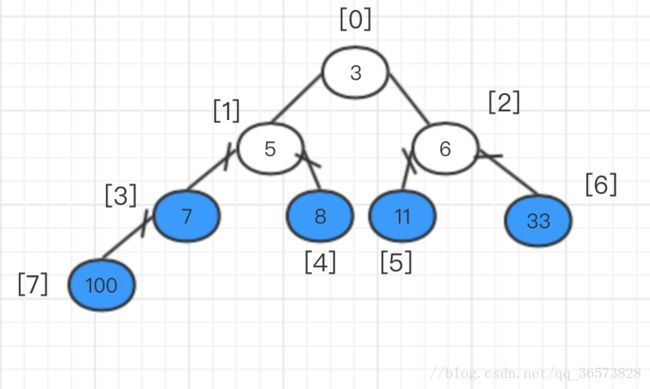
此时调整完堆后，再将堆顶元素和最后一个元素互换位置，即将11和6互换，再将11至于完全二叉树外。

此时再进行完全二叉树的调整，即就是白色填充的元素进行调整。从根开始，按照上面的方法。

此时又是一个调整好的堆，将堆顶元素和最后一个元素互换。

再进行完全二叉树的调整

此时再进行堆顶元素和最后一个元素的互换

再进行完全二叉树的调整

最后进行堆顶元素的互换：

最后一次调整：

最后一次堆顶元素交换：

此时数组已经是一个有序数组，是一个生序数组，用for循环输出即可。

---

代码实现（C语言）

#include

void swap(int *a, int *b)
{
    int p;
    p = *a;
    *a = *b;
    *b = p;
}

void adjustheap(int *arr, int i, int len)
{
    int j = i*2+1;
    while(j < len)
    {
        if(j+11]) //建立大堆,若左孩子小于右孩子,将j取值为右孩子的下标,右孩子再与父结点比较
        {
            j++;
        }
        //将左右孩子中，数值最大的与父结点进行比较,若孩子结点比父结点小,说明父结点的数值比左右孩子都大,不需要交换
        if(arr[i] > arr[j])
        {
            break;//说明该父结点和其孩子结点调整结束，退出循环，从下一个父结点调整
        }
        swap(&arr[i], &arr[j]);
        //交换之后还要考虑该目前j结点与自己的孩子结点的数值比较，还要进行调整,将i当前结点换成j结点所在位置
        i = j;
        j = 2*i+1;
    }
}

void makeheap(int *arr, int n)
{
    int i;
    for(i=n/2-1; i>=0; i--)//要从最后一个父节点开始调整堆
    {
        adjustheap(arr, i, n);
    }
}

void heapsort(int *arr, int len)
{
    int i = 0;
    makeheap(arr, len);
    //每次排出最大的一个元素之后，将该元素排除在堆外,调整堆后交换堆顶元素和堆的最后一个元素
    for(i=len-1; i>=0; i--)//所以要从元素最后一个开始
    {
        swap(&arr[i], &arr[0]);
        /*交换好堆后,重新调整堆*/
        adjustheap(arr, 0, i);      
    }
}

int main()
{
    int a[8]={100,33,3,7,11,6,8,5};
    int n = 8;
    heapsort(a, n);
    for(int i=0; i<8; i++)
    {
        printf("%d ",a[i]);
    }
    printf("\n");
    return 0;
}