第十三周项目四
/*
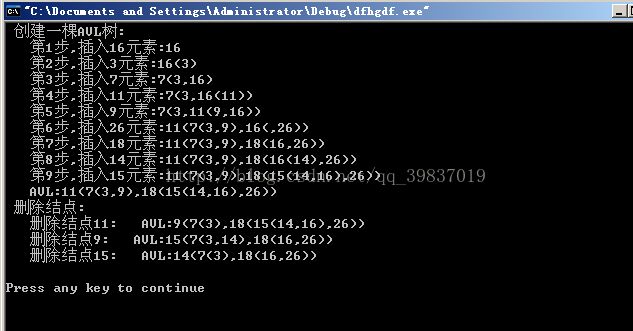
二、测试结果截图如下:
*Copyright (c)2017,烟台大学计算机与控制工程学院
*All rights reservrd.
*作者:张思琦
*完成时间:2017年12月7日
*版本号:v1.0
*问题描述:运行并本周视频中所讲过的算法,观察结果并领会算法。
认真阅读并验证平衡二叉树相关算法。
(1)由整数序列{43,52,75,24,10,38,67,55,63,60}构造AVL树;
(2)输出用括号法表示的AVL树;
(3)查找关键字55;
(4)分别删除43和55,输出删除后用括号法表示的二叉排序树。
一、代码如下:
- #include
- typedef int KeyType; //定义关键字类型
- typedef char InfoType;
- typedef struct node //记录类型
- {
- KeyType key; //关键字项
- int bf; //平衡因子
- InfoType data; //其他数据域
- struct node *lchild,*rchild; //左右孩子指针
- } BSTNode;
- void LeftProcess(BSTNode *&p,int &taller)
- //对以指针p所指结点为根的二叉树作左平衡旋转处理,本算法结束时,指针p指向新的根结点
- {
- BSTNode *p1,*p2;
- if (p->bf==0) //原本左、右子树等高,现因左子树增高而使树增高
- {
- p->bf=1;
- taller=1;
- }
- else if (p->bf==-1) //原本右子树比左子树高,现左、右子树等高
- {
- p->bf=0;
- taller=0;
- }
- else //原本左子树比右子树高,需作左子树的平衡处理
- {
- p1=p->lchild; //p指向*p的左子树根结点
- if (p1->bf==1) //新结点插入在*b的左孩子的左子树上,要作LL调整
- {
- p->lchild=p1->rchild;
- p1->rchild=p;
- p->bf=p1->bf=0;
- p=p1;
- }
- else if (p1->bf==-1) //新结点插入在*b的左孩子的右子树上,要作LR调整
- {
- p2=p1->rchild;
- p1->rchild=p2->lchild;
- p2->lchild=p1;
- p->lchild=p2->rchild;
- p2->rchild=p;
- if (p2->bf==0) //新结点插在*p2处作为叶子结点的情况
- p->bf=p1->bf=0;
- else if (p2->bf==1) //新结点插在*p2的左子树上的情况
- {
- p1->bf=0;
- p->bf=-1;
- }
- else //新结点插在*p2的右子树上的情况
- {
- p1->bf=1;
- p->bf=0;
- }
- p=p2;
- p->bf=0; //仍将p指向新的根结点,并置其bf值为0
- }
- taller=0;
- }
- }
- void RightProcess(BSTNode *&p,int &taller)
- //对以指针p所指结点为根的二叉树作右平衡旋转处理,本算法结束时,指针p指向新的根结点
- {
- BSTNode *p1,*p2;
- if (p->bf==0) //原本左、右子树等高,现因右子树增高而使树增高
- {
- p->bf=-1;
- taller=1;
- }
- else if (p->bf==1) //原本左子树比右子树高,现左、右子树等高
- {
- p->bf=0;
- taller=0;
- }
- else //原本右子树比左子树高,需作右子树的平衡处理
- {
- p1=p->rchild; //p指向*p的右子树根结点
- if (p1->bf==-1) //新结点插入在*b的右孩子的右子树上,要作RR调整
- {
- p->rchild=p1->lchild;
- p1->lchild=p;
- p->bf=p1->bf=0;
- p=p1;
- }
- else if (p1->bf==1) //新结点插入在*p的右孩子的左子树上,要作RL调整
- {
- p2=p1->lchild;
- p1->lchild=p2->rchild;
- p2->rchild=p1;
- p->rchild=p2->lchild;
- p2->lchild=p;
- if (p2->bf==0) //新结点插在*p2处作为叶子结点的情况
- p->bf=p1->bf=0;
- else if (p2->bf==-1) //新结点插在*p2的右子树上的情况
- {
- p1->bf=0;
- p->bf=1;
- }
- else //新结点插在*p2的左子树上的情况
- {
- p1->bf=-1;
- p->bf=0;
- }
- p=p2;
- p->bf=0; //仍将p指向新的根结点,并置其bf值为0
- }
- taller=0;
- }
- }
- int InsertAVL(BSTNode *&b,KeyType e,int &taller)
- /*若在平衡的二叉排序树b中不存在和e有相同关键字的结点,则插入一个
- 数据元素为e的新结点,并返回1,否则返回0。若因插入而使二叉排序树
- 失去平衡,则作平衡旋转处理,布尔变量taller反映b长高与否*/
- {
- if(b==NULL) //原为空树,插入新结点,树“长高”,置taller为1
- {
- b=(BSTNode *)malloc(sizeof(BSTNode));
- b->key=e;
- b->lchild=b->rchild=NULL;
- b->bf=0;
- taller=1;
- }
- else
- {
- if (e==b->key) //树中已存在和e有相同关键字的结点则不再插入
- {
- taller=0;
- return 0;
- }
- if (e
key) //应继续在*b的左子树中进行搜索 - {
- if ((InsertAVL(b->lchild,e,taller))==0) //未插入
- return 0;
- if (taller==1) //已插入到*b的左子树中且左子树“长高”
- LeftProcess(b,taller);
- }
- else //应继续在*b的右子树中进行搜索
- {
- if ((InsertAVL(b->rchild,e,taller))==0) //未插入
- return 0;
- if (taller==1) //已插入到b的右子树且右子树“长高”
- RightProcess(b,taller);
- }
- }
- return 1;
- }
- void DispBSTree(BSTNode *b) //以括号表示法输出AVL
- {
- if (b!=NULL)
- {
- printf("%d",b->key);
- if (b->lchild!=NULL || b->rchild!=NULL)
- {
- printf("(");
- DispBSTree(b->lchild);
- if (b->rchild!=NULL) printf(",");
- DispBSTree(b->rchild);
- printf(")");
- }
- }
- }
- void LeftProcess1(BSTNode *&p,int &taller) //在删除结点时进行左处理
- {
- BSTNode *p1,*p2;
- if (p->bf==1)
- {
- p->bf=0;
- taller=1;
- }
- else if (p->bf==0)
- {
- p->bf=-1;
- taller=0;
- }
- else //p->bf=-1
- {
- p1=p->rchild;
- if (p1->bf==0) //需作RR调整
- {
- p->rchild=p1->lchild;
- p1->lchild=p;
- p1->bf=1;
- p->bf=-1;
- p=p1;
- taller=0;
- }
- else if (p1->bf==-1) //需作RR调整
- {
- p->rchild=p1->lchild;
- p1->lchild=p;
- p->bf=p1->bf=0;
- p=p1;
- taller=1;
- }
- else //需作RL调整
- {
- p2=p1->lchild;
- p1->lchild=p2->rchild;
- p2->rchild=p1;
- p->rchild=p2->lchild;
- p2->lchild=p;
- if (p2->bf==0)
- {
- p->bf=0;
- p1->bf=0;
- }
- else if (p2->bf==-1)
- {
- p->bf=1;
- p1->bf=0;
- }
- else
- {
- p->bf=0;
- p1->bf=-1;
- }
- p2->bf=0;
- p=p2;
- taller=1;
- }
- }
- }
- void RightProcess1(BSTNode *&p,int &taller) //在删除结点时进行右处理
- {
- BSTNode *p1,*p2;
- if (p->bf==-1)
- {
- p->bf=0;
- taller=-1;
- }
- else if (p->bf==0)
- {
- p->bf=1;
- taller=0;
- }
- else //p->bf=1
- {
- p1=p->lchild;
- if (p1->bf==0) //需作LL调整
- {
- p->lchild=p1->rchild;
- p1->rchild=p;
- p1->bf=-1;
- p->bf=1;
- p=p1;
- taller=0;
- }
- else if (p1->bf==1) //需作LL调整
- {
- p->lchild=p1->rchild;
- p1->rchild=p;
- p->bf=p1->bf=0;
- p=p1;
- taller=1;
- }
- else //需作LR调整
- {
- p2=p1->rchild;
- p1->rchild=p2->lchild;
- p2->lchild=p1;
- p->lchild=p2->rchild;
- p2->rchild=p;
- if (p2->bf==0)
- {
- p->bf=0;
- p1->bf=0;
- }
- else if (p2->bf==1)
- {
- p->bf=-1;
- p1->bf=0;
- }
- else
- {
- p->bf=0;
- p1->bf=1;
- }
- p2->bf=0;
- p=p2;
- taller=1;
- }
- }
- }
- void Delete2(BSTNode *q,BSTNode *&r,int &taller)
- //由DeleteAVL()调用,用于处理被删结点左右子树均不空的情况
- {
- if (r->rchild==NULL)
- {
- q->key=r->key;
- q=r;
- r=r->lchild;
- free(q);
- taller=1;
- }
- else
- {
- Delete2(q,r->rchild,taller);
- if (taller==1)
- RightProcess1(r,taller);
- }
- }
- int DeleteAVL(BSTNode *&p,KeyType x,int &taller) //在AVL树p中删除关键字为x的结点
- {
- int k;
- BSTNode *q;
- if (p==NULL)
- return 0;
- else if (x
key) - {
- k=DeleteAVL(p->lchild,x,taller);
- if (taller==1)
- LeftProcess1(p,taller);
- return k;
- }
- else if (x>p->key)
- {
- k=DeleteAVL(p->rchild,x,taller);
- if (taller==1)
- RightProcess1(p,taller);
- return k;
- }
- else //找到了关键字为x的结点,由p指向它
- {
- q=p;
- if (p->rchild==NULL) //被删结点右子树为空
- {
- p=p->lchild;
- free(q);
- taller=1;
- }
- else if (p->lchild==NULL) //被删结点左子树为空
- {
- p=p->rchild;
- free(q);
- taller=1;
- }
- else //被删结点左右子树均不空
- {
- Delete2(q,q->lchild,taller);
- if (taller==1)
- LeftProcess1(q,taller);
- p=q;
- }
- return 1;
- }
- }
- int main()
- {
- BSTNode *b=NULL;
- int i,j,k;
- KeyType a[]= {16,3,7,11,9,26,18,14,15},n=9; //例10.5
- printf(" 创建一棵AVL树:\n");
- for(i=0; i
- {
- printf(" 第%d步,插入%d元素:",i+1,a[i]);
- InsertAVL(b,a[i],j);
- DispBSTree(b);
- printf("\n");
- }
- printf(" AVL:");
- DispBSTree(b);
- printf("\n");
- printf(" 删除结点:\n"); //例10.6
- k=11;
- printf(" 删除结点%d:",k);
- DeleteAVL(b,k,j);
- printf(" AVL:");
- DispBSTree(b);
- printf("\n");
- k=9;
- printf(" 删除结点%d:",k);
- DeleteAVL(b,k,j);
- printf(" AVL:");
- DispBSTree(b);
- printf("\n");
- k=15;
- printf(" 删除结点%d:",k);
- DeleteAVL(b,k,j);
- printf(" AVL:");
- DispBSTree(b);
- printf("\n\n");
- return 0;
- }
#include
#include
typedef int KeyType; //定义关键字类型
typedef char InfoType;
typedef struct node //记录类型
{
KeyType key; //关键字项
int bf; //平衡因子
InfoType data; //其他数据域
struct node *lchild,*rchild; //左右孩子指针
} BSTNode;
void LeftProcess(BSTNode *&p,int &taller)
//对以指针p所指结点为根的二叉树作左平衡旋转处理,本算法结束时,指针p指向新的根结点
{
BSTNode *p1,*p2;
if (p->bf==0) //原本左、右子树等高,现因左子树增高而使树增高
{
p->bf=1;
taller=1;
}
else if (p->bf==-1) //原本右子树比左子树高,现左、右子树等高
{
p->bf=0;
taller=0;
}
else //原本左子树比右子树高,需作左子树的平衡处理
{
p1=p->lchild; //p指向*p的左子树根结点
if (p1->bf==1) //新结点插入在*b的左孩子的左子树上,要作LL调整
{
p->lchild=p1->rchild;
p1->rchild=p;
p->bf=p1->bf=0;
p=p1;
}
else if (p1->bf==-1) //新结点插入在*b的左孩子的右子树上,要作LR调整
{
p2=p1->rchild;
p1->rchild=p2->lchild;
p2->lchild=p1;
p->lchild=p2->rchild;
p2->rchild=p;
if (p2->bf==0) //新结点插在*p2处作为叶子结点的情况
p->bf=p1->bf=0;
else if (p2->bf==1) //新结点插在*p2的左子树上的情况
{
p1->bf=0;
p->bf=-1;
}
else //新结点插在*p2的右子树上的情况
{
p1->bf=1;
p->bf=0;
}
p=p2;
p->bf=0; //仍将p指向新的根结点,并置其bf值为0
}
taller=0;
}
}
void RightProcess(BSTNode *&p,int &taller)
//对以指针p所指结点为根的二叉树作右平衡旋转处理,本算法结束时,指针p指向新的根结点
{
BSTNode *p1,*p2;
if (p->bf==0) //原本左、右子树等高,现因右子树增高而使树增高
{
p->bf=-1;
taller=1;
}
else if (p->bf==1) //原本左子树比右子树高,现左、右子树等高
{
p->bf=0;
taller=0;
}
else //原本右子树比左子树高,需作右子树的平衡处理
{
p1=p->rchild; //p指向*p的右子树根结点
if (p1->bf==-1) //新结点插入在*b的右孩子的右子树上,要作RR调整
{
p->rchild=p1->lchild;
p1->lchild=p;
p->bf=p1->bf=0;
p=p1;
}
else if (p1->bf==1) //新结点插入在*p的右孩子的左子树上,要作RL调整
{
p2=p1->lchild;
p1->lchild=p2->rchild;
p2->rchild=p1;
p->rchild=p2->lchild;
p2->lchild=p;
if (p2->bf==0) //新结点插在*p2处作为叶子结点的情况
p->bf=p1->bf=0;
else if (p2->bf==-1) //新结点插在*p2的右子树上的情况
{
p1->bf=0;
p->bf=1;
}
else //新结点插在*p2的左子树上的情况
{
p1->bf=-1;
p->bf=0;
}
p=p2;
p->bf=0; //仍将p指向新的根结点,并置其bf值为0
}
taller=0;
}
}
int InsertAVL(BSTNode *&b,KeyType e,int &taller)
/*若在平衡的二叉排序树b中不存在和e有相同关键字的结点,则插入一个
数据元素为e的新结点,并返回1,否则返回0。若因插入而使二叉排序树
失去平衡,则作平衡旋转处理,布尔变量taller反映b长高与否*/
{
if(b==NULL) //原为空树,插入新结点,树“长高”,置taller为1
{
b=(BSTNode *)malloc(sizeof(BSTNode));
b->key=e;
b->lchild=b->rchild=NULL;
b->bf=0;
taller=1;
}
else
{
if (e==b->key) //树中已存在和e有相同关键字的结点则不再插入
{
taller=0;
return 0;
}
if (ekey) //应继续在*b的左子树中进行搜索
{
if ((InsertAVL(b->lchild,e,taller))==0) //未插入
return 0;
if (taller==1) //已插入到*b的左子树中且左子树“长高”
LeftProcess(b,taller);
}
else //应继续在*b的右子树中进行搜索
{
if ((InsertAVL(b->rchild,e,taller))==0) //未插入
return 0;
if (taller==1) //已插入到b的右子树且右子树“长高”
RightProcess(b,taller);
}
}
return 1;
}
void DispBSTree(BSTNode *b) //以括号表示法输出AVL
{
if (b!=NULL)
{
printf("%d",b->key);
if (b->lchild!=NULL || b->rchild!=NULL)
{
printf("(");
DispBSTree(b->lchild);
if (b->rchild!=NULL) printf(",");
DispBSTree(b->rchild);
printf(")");
}
}
}
void LeftProcess1(BSTNode *&p,int &taller) //在删除结点时进行左处理
{
BSTNode *p1,*p2;
if (p->bf==1)
{
p->bf=0;
taller=1;
}
else if (p->bf==0)
{
p->bf=-1;
taller=0;
}
else //p->bf=-1
{
p1=p->rchild;
if (p1->bf==0) //需作RR调整
{
p->rchild=p1->lchild;
p1->lchild=p;
p1->bf=1;
p->bf=-1;
p=p1;
taller=0;
}
else if (p1->bf==-1) //需作RR调整
{
p->rchild=p1->lchild;
p1->lchild=p;
p->bf=p1->bf=0;
p=p1;
taller=1;
}
else //需作RL调整
{
p2=p1->lchild;
p1->lchild=p2->rchild;
p2->rchild=p1;
p->rchild=p2->lchild;
p2->lchild=p;
if (p2->bf==0)
{
p->bf=0;
p1->bf=0;
}
else if (p2->bf==-1)
{
p->bf=1;
p1->bf=0;
}
else
{
p->bf=0;
p1->bf=-1;
}
p2->bf=0;
p=p2;
taller=1;
}
}
}
void RightProcess1(BSTNode *&p,int &taller) //在删除结点时进行右处理
{
BSTNode *p1,*p2;
if (p->bf==-1)
{
p->bf=0;
taller=-1;
}
else if (p->bf==0)
{
p->bf=1;
taller=0;
}
else //p->bf=1
{
p1=p->lchild;
if (p1->bf==0) //需作LL调整
{
p->lchild=p1->rchild;
p1->rchild=p;
p1->bf=-1;
p->bf=1;
p=p1;
taller=0;
}
else if (p1->bf==1) //需作LL调整
{
p->lchild=p1->rchild;
p1->rchild=p;
p->bf=p1->bf=0;
p=p1;
taller=1;
}
else //需作LR调整
{
p2=p1->rchild;
p1->rchild=p2->lchild;
p2->lchild=p1;
p->lchild=p2->rchild;
p2->rchild=p;
if (p2->bf==0)
{
p->bf=0;
p1->bf=0;
}
else if (p2->bf==1)
{
p->bf=-1;
p1->bf=0;
}
else
{
p->bf=0;
p1->bf=1;
}
p2->bf=0;
p=p2;
taller=1;
}
}
}
void Delete2(BSTNode *q,BSTNode *&r,int &taller)
//由DeleteAVL()调用,用于处理被删结点左右子树均不空的情况
{
if (r->rchild==NULL)
{
q->key=r->key;
q=r;
r=r->lchild;
free(q);
taller=1;
}
else
{
Delete2(q,r->rchild,taller);
if (taller==1)
RightProcess1(r,taller);
}
}
int DeleteAVL(BSTNode *&p,KeyType x,int &taller) //在AVL树p中删除关键字为x的结点
{
int k;
BSTNode *q;
if (p==NULL)
return 0;
else if (xkey)
{
k=DeleteAVL(p->lchild,x,taller);
if (taller==1)
LeftProcess1(p,taller);
return k;
}
else if (x>p->key)
{
k=DeleteAVL(p->rchild,x,taller);
if (taller==1)
RightProcess1(p,taller);
return k;
}
else //找到了关键字为x的结点,由p指向它
{
q=p;
if (p->rchild==NULL) //被删结点右子树为空
{
p=p->lchild;
free(q);
taller=1;
}
else if (p->lchild==NULL) //被删结点左子树为空
{
p=p->rchild;
free(q);
taller=1;
}
else //被删结点左右子树均不空
{
Delete2(q,q->lchild,taller);
if (taller==1)
LeftProcess1(q,taller);
p=q;
}
return 1;
}
}
int main()
{
BSTNode *b=NULL;
int i,j,k;
KeyType a[]= {16,3,7,11,9,26,18,14,15},n=9; //例10.5
printf(" 创建一棵AVL树:\n");
for(i=0; i 二、测试结果截图如下: