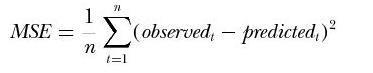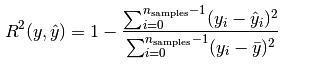回归模型的评估指标
回归模型评估有三种方法,分别是:平均绝对值误差、均方误差和R平方值,如表1所示:
| 指标 | 描述 | metrics方法 |
|---|---|---|
| Mean Absolute Error(MAE) | 平均绝对误差 | from sklearn.metrics import mean_absolute_error |
| Mean Square Error(MSE) | 平均方差 | from sklearn.metrics import mean_squared_error |
| R-Squared | R平方值 | from sklearn.metrics import r2_score |
7.8.1 平均绝对误差
平均绝对误差(MAE)就是指预测值与真实值之间平均相差多大,公式如下:
图1 平均绝对误差(MAE)
其中,fi是预测值,yi是真实值,ei=|fi-yi|即是绝对误差。
sklearn库的metrics模块提供了mean_absolute_error方法,用来评估回归模型,首先建立数据集和线性回归模型对测试集数据进行预测,示例代码:
# 创建数据集,其中矩阵X表示特征值,向量y表示所属类目标记值
import numpy as np
X=np.random.random((10,5))
y=np.random.randn(10,1)
# 数据切分为训练集和测试集
from sklearn.cross_validation import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
# 利用线性回归模型对数据进行拟合
from sklearn.linear_model import LinearRegression
lr=LinearRegression(normalize=True)
lr.fit(X_train,y_train)
# 对测试集数据预测
y_pred = lr.predict(X_test)
print(y_pred)
print(y_test)
运行结果:
[[-1.34421249]
[-0.07903063]
[-1.56484151]]
[[-0.3252582 ]
[-1.31381548]
[ 0.00690077]]
然后利用引入平均绝对误差方法对模型进行评估,示例代码:
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred)
运行结果:
1.275160473519662
7.8.2 平均方差
均方误差是指参数估计值与参数真值之差平方的期望值,记为MSE。MSE是衡量平均误差的一种较方便的方法,MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。均方误差的公式如下:
图6 均方误差
sklearn库的metrics模块提供了mean_squared_error方法,用来对回归模型进行均方误差评估,示例代码:
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, y_pred)
运行结果:
1.6777784223212659
7.8.3 R平方值
它是表征回归方程在多大程度上解释了因变量的变化,或者说方程对观测值的拟合程度如何。其公式如图7所示:
图7 R平均值
sklearn库的metrics模块提供了r2_score方法,用来对回归模型进行R平方值评估,示例代码:
from sklearn.metrics import r2_score
r2_score(y_test, y_pred)
运行结果:
-4.3321743235578118
7.:8.4 交叉验证(Cross-Validation)
交叉验证,有的时候也称作循环估计(Rotation Estimation),是一种统计学上将数据样本切割成较小子集的实用方法,该理论是由Seymour Geisser提出的。在给定的建模样本中,拿出大部分样本进行建模型,留小部分样本用刚建立的模型进行预报,并求这小部分样本的预报误差,记录它们的平方加和。这个过程一直进行,直到所有的样本都被预报了一次而且仅被预报一次。把每个样本的预报误差平方加和,称为PRESS(predicted Error Sum of Squares)。
交叉验证的基本思想是把在某种意义下将原始数据(dataset)进行分组,一部分做为训练集(train set),另一部分做为验证集(validation set or test set)。首先用训练集对分类器进行训练,再利用验证集来测试训练得到的模型(model),以此来做为评价分类器的性能指标。
无论分类还是回归模型,都可以利用交叉验证,进行模型评估,示例代码:
from sklearn.cross_validation import cross_val_score
print(cross_val_score(knn, X_train, y_train, cv=4))
print(cross_cal_score(lr, X, y, cv=2))