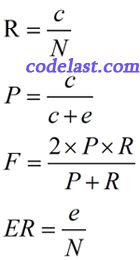中文分词的评估及实现

这篇文章理论部分来自

https://www.codelast.com/%E5%8E%9F%E5%88%9B%E4%B8%AD%E6%96%87%E5%88%86%E8%AF%8D%E5%99%A8%E5%88%86%E8%AF%8D%E6%95%88%E6%9E%9C%E7%9A%84%E8%AF%84%E6%B5%8B%E6%96%B9%E6%B3%95/

实现是我自己写的。

实现在最下面：

【2】评价指标
精度（Precision）、召回率（Recall）、F值（F-mesure）是用于评价一个信息检索系统的质量的3个主要指标，以下分别简记为P，R和F。同时，还可以把错误率（Error Rate）作为分词效果的评价标准之一（以下简记为ER）。
直观地说，精度表明了分词器分词的准确程度；召回率也可认为是“查全率”，表明了分词器切分正确的词有多么全；F值综合反映整体的指标；错误率表明了分词器分词的错误程度。
P、R、F越大越好，ER越小越好。一个完美的分词器的P、R、F值均为1，ER值为0。
通常，召回率和精度这两个指标会相互制约。

 

例如，还是拿上面那句话作为例子：“科学技术是第一生产力”（黄金标准为“科学技术 是 第一 生产力”），假设有一个分词器很极端，把几乎所有前后相连的词的组合都作为分词结果，就像这个样子：“科学 技术 科学技术 是 是第一 第一生产力 生产力”，那么毫无疑问，它切分正确的词已经覆盖了黄金标准中的所有词，即它的召回率（Recall）很高。但是由于它分错了很多词，因此，它的精度（Precision）很低。

因此，召回率和精度这二者有一个平衡点，我们希望它们都是越大越好，但通常不容易做到都大。

为了陈述上述指标的计算方法，先定义如下数据：
N ：黄金标准分割的单词数
e ：分词器错误标注的单词数
c ：分词器正确标注的单词数

则以上各指标的计算公式如下：

【3】正确及错误标注的计数算法

 

如上所述，我们要先计算出e和c，才能计算出各指标值。 e 和 c 是按如下算法来统计的：

在“黄金标准”和“待评测的结果”中，理论上，除了分词后添加的空格之外，它们所有的文字都是相同的；唯一的不同就在于那些有差异的分词结果的位置上。例如，“计算机 是个 好东西”（黄金标准）与“计算机 是 个 好东西”（待评测的结果）的差异就在于“是个”与“是 个”的差异，其余分词结果都是相同的。因此，只需要找到这种差异的个数，就可以统计出分词器正确标注了多少个词、错误标注了多少个词。
 

以下面的分词结果为例：

“计算机 总是 有问题”——黄金标准

“计算机 总 是 有问题”——待评测的结果
 

给分出来的每个词都做位置的标记（位置从1开始）：

(1,4)，(4,6)，(6,9) ——黄金标准

(1,4)，(4,5)，(5,6)，(6,9) ——待评测的结果
 

那么我们会发现，(1,4)和(6,9)这两个词是相同的（即“计算机”和“有问题”），而差异在于(4,6)和(4,5)，(5,6)（即“总是”和“总 是”），因此，我们只需要比较这两个标注结果中的差异数，就可以知道分词器正确、错误地标注了多少个单词。在此例中，正确的标注的单词数为2，错误标注的单词数为2。
 

需要说明的是：在此例中，也可以认为错误标注的单词数为1（即“总是”与“总 是”的差异），按照最大错误数来算会使错误率升高（在分词精度很差的情况下，可能会导致ER>100%），不过，在所有分词器都使用同一标准来评测的情况下，也就会很公平，并不会影响到最终的结论。

下面给一个简单的java实现：

package com.outsider.model.metric;

import java.util.ArrayList;
import java.util.List;

/**
 * 分词评估
 * @author outsider
 * 比如 
 * 	黄金标准:计算机 总是 有问题
 *	分词结果: 计算机 总 是 有问题
 *	对黄金标准中和分词器中的的每一个词做标注
 *	黄金标准:(0,2),(3,4),(5,7)
 *	分词器:(0,2),(3),(4),(5,7)
 *	对比发现分词器中标注正确的由2个，而标注错误的可以认为是1个，也可以认为是2个
 *	在下面的评估算法中认为如果预测标注错误的将一个词标记成n个，那么错误标注也是n个，而不是1个
 *	如果预测结果错误的将多个词粘在一起，那么标注错错误认为是1个
 *
 */
public class SegmenterEvaluation {
	/**
	 * 召回率：查全率，越大越好
	 */
	private double recallScore;
	/**
	 * 精度：准确率，越大越好
	 */
	private double precisionScore;
	/**
	 * f得分：综合评估，越大越好
	 */
	private double fMeasureScore;
	/**
	 * 错误率：越小越好
	 */
	private double errorRate;
	public void score(String[] right, String[] predict) {
		int rightCount = rightCount(right, predict);
		this.recallScore = rightCount*1.0 / right.length;
		this.precisionScore = rightCount*1.0 / predict.length;
		this.fMeasureScore = (2*precisionScore*recallScore) / (precisionScore + recallScore);
		this.errorRate = (predict.length -rightCount*1.0) / right.length;
	}
	
	public void printScore() {
		System.out.println("召回率:"+this.recallScore+",精准率:"+this.precisionScore+",F值:"+this.fMeasureScore+",错误率:"+this.errorRate);
	}
	
	/**
	 * 统计分词结果中正确的个数
	 * @param right 正确的分词结果
	 * @param predict 预测的分词结果
	 * @return
	 */
	public int rightCount(String[] right, String[] predict) {
		List rightNodes = buildNodes(right);
		List predictNodes = buildNodes(predict);
		//统计标注正确的个数
		int count = 0;
		for(int i = 0; i < predictNodes.size(); i++) {
			if(rightNodes.contains(predictNodes.get(i))) {
				count++;
			}
		}
		return count;
	}
	
	public List buildNodes(String[] words){
		List nodes = new ArrayList<>();
		int last = 0;
		for(int i = 0; i < words.length; i++) {
			WordNode node = new WordNode(last, last + words[i].length() - 1);
			nodes.add(node);
			last = node.end + 1;
			
		}
		return nodes;
	}
	
	
	/**
	 * 描述一个词在一个分词结果集中的位置
	 * @author outsider
	 *
	 */
	public static class WordNode{
		//开始位置和结尾位置都包括
		public int start;//词的开始位置
		public int end;//词的结尾位置
		
		public WordNode(int start, int end) {
			super();
			this.start = start;
			this.end = end;
		}

		@Override
		public boolean equals(Object obj) {
			WordNode node = (WordNode) obj;
			if(this.start == node.start && this.end == node.end)
				return true;
			return false;
		}
		
		@Override
		public String toString() {
			return "("+start+","+end+")";
		}
	}


	public double getRecallScore() {
		return recallScore;
	}
	public double getPrecisionScore() {
		return precisionScore;
	}
	public double getfMeasureScore() {
		return fMeasureScore;
	}
	public double getErrorRate() {
		return errorRate;
	}
    public static void main(String[] args) {
		String[] right = new String[] {"计算机","总是","出问题"};
		String[] predict = new String[] {"计算机","总","是","出问题"};
		SegmenterEvaluation evaluation = new SegmenterEvaluation();
		evaluation.score(right, predict);
		evaluation.printScore();
	}
	
}