dijkstra+Floyd图论算法的校内应急路线规划Matlab+Haskell打开方式
学习过图论相关算法,闲着技痒,根据校区的地形图,对校内的区域路网进行规划,设计,建模,建立描述某大学校区的加权无向图,主要提供dijkstra+Floyd图论算法的校内应急路线规划Matlab+Haskell打开方式.
我的校区的图形分布,和某校区的路线,根据不同地区的学生活动区域,就近分组,对地图进行适当的简化,分组情况如下:
1,2,3公寓;4+11公寓;3餐厅+9公寓;4餐厅+8公寓;13公寓;5餐+7公寓+保卫办+快递站+交通楼;5,6公寓+1餐;大虾;图书馆;二教;致远超市;一教;三教前路口;逸夫楼+管理学院;路口1;路口2;体育馆;篮球场入口;体育入口;东门;西门;南门;北门;能源动力大楼+工训中心+工厂;工程小院;路口三+交通楼;计算机中心
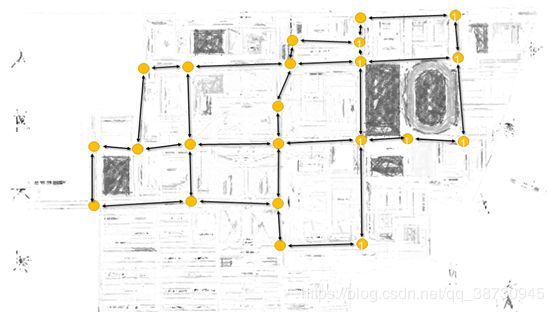
图1-1
首先,搜集资料,得到某校区的卫星地图的绿化地图,利用计算机软件Matlab等对原图像进行图像处理,如图1-1所示,分组完毕,得到真正的交通路线,就近选择交通路口作为节点,链接重要交通地形的节点。
以上图为例子,本文可以根据原图像得到初步的地图分布,结合相关数据,不难得到某校区地形的基本路线图。
根据基本路线图,可以建立图论相关简化模型,然后
1.4 建立校园地理特征的图论模型
针对最常见的学生活动路线进行分析,把最关键的交通路口作为结点,建立关键的工作节点,链接不同的节点,根据校区内复杂的交通路网,对真实问题中复杂的交通路网进行数学语言的简化描述,根据百度地图测量节点之间的实际距离,以米为单位标注为图中节点之间的权重,可以得到加权无向图,如下所示:

图1-3
路网说明,上面把某校区的实际区域分布抽象为37个没有空间面积的质点,质点之间的数字代表质点之间的距离(单位为米)。其中注释比较重要的几个地点,
1 西门;
15 大北门
21 小北门
35 东门
36 南门
注:因为小南门一般不通车,或者学生很少路过,车流量,人流量非常小,故忽略此地。同样的道理,校内有一些区域的地形会予以忽略。
图1-3是一个加权有向图
D = ( V , A ) D=(V,A) D=(V,A)
其中, V = V 1 , V 2 , . . . , V 3 7 V= {V_1,V_2,...,V_37} V=V1,V2,...,V37
A = ( V 1 , V 3 ) , ( V 1 , V 4 ) , . . . . . . , ( V 1 2 , V 3 7 ) , ( V 5 , V 3 7 ) , ( V 9 , V 3 7 ) A={(V_1,V_3),(V_1,V_4),......,(V_12,V_37),(V_5,V_37),(V_9,V_37)} A=(V1,V3),(V1,V4),......,(V12,V37),(V5,V37),(V9,V37)
在图与网络分析的应用中,将面临一个问题——如何分析、计算一个较大型的网络,这当然需借助快速的计算工具——计算机。那么,如何将一个图表示在计算机中,或者,如何在计算机中存储一个图呢?现在已有很多存储的方法,但最基本的方法就是采用矩阵来表示一个图,图的矩阵表示也根据所关心的问题不同而有——邻接矩阵、关联矩阵、权矩阵等。
根据Matlab处理矩阵的特性,把图形存储为三种格式:
一 ,邻接矩阵
邻接矩阵——对于图 D = ( V , A ) D=(V,A) D=(V,A), ∣ V ∣ = n |V|=n ∣V∣=n, ∣ E ∣ = m |E|=m ∣E∣=m
有 m ∗ n m*n m∗n 阶方阵 A = ( a i j ) A=(a_{ij}) A=(aij)
其中:
a i j = { k 当 且 仅 当 i j 有 边 0 a_{ij}=\left\{ \begin{aligned} k & 当且仅当ij有边\\ 0 \end{aligned} \right. aij={k0当且仅当ij有边
二 ,关联矩阵
关联矩阵——对于图 D = ( V , A ) D=(V,A) D=(V,A), ∣ V ∣ = n |V|=n ∣V∣=n, ∣ E ∣ = m |E|=m ∣E∣=m
有 m ∗ n m*n m∗n 阶方阵 A = ( a i j ) A=(a_{ij}) A=(aij)
其中:
a i j = { 1 当 且 仅 当 点 v i 是 e j 边 的 两 个 端 点 2 当 且 仅 当 点 v i 是 e j 边 的 一 个 端 点 0 a_{ij}=\left\{ \begin{array}{rcl} 1 & 当且仅当点v_i是e_j边的两个端点\\ 2 & 当且仅当点v_i是e_j边的一个端点\\ 0 \end{array} \right. aij=⎩⎨⎧120当且仅当点vi是ej边的两个端点当且仅当点vi是ej边的一个端点三 ,权矩阵
1.4 模型假设
为了有效的刻画分块区域之间的距离,分析当前交通分布的路网现况下,保卫办的工作人员到每个地区
1 不考虑各个区域的实际尺寸,简化为点进行处理
2 把每个建筑物正门作为建筑的位置,以两个建筑物的前门的距离作为点之间的权重值。
3 不考虑突发性赛车或者校区内施工等意外或者事故导致的“道路不同的现象”。
4 暂时不考虑人口,上课路线,交通状况,人流分布,或者特殊的社会活动等因素,仅仅从校区内路网交通现况进行考虑。
基于dijstra算法最短路问题的道路分析
得到任意两点之间最短路程,为警备人员在最短时间到达现场提供最短路线规划,模型求解和调度实例
因为Dijkstra算法是典型的“单源最短路”问题,而需要在任意两点得到最短路的话,需要比较当出现中继点的时候,是否出现经过中继点的时候能比两点直接相连更加近,如果能,则更新距离矩阵,得到最终答案,记录路线,这样一次计算,可以得到图论中任意两点的最短距离路线的优化结果!
举例说明一下,假设一天,小北门的变压站火灾爆炸(真事-_-#),保卫办大哥必须及时保证学生的安全,在最短的时间感到小北门去,从37保卫办需要紧急去往21小北门去救援,对应在matlab的代码是
[distance,path] = Dijk(W,37,21)
瞬间,Matlab给出路线规划是path = 37 9 8 16 15 21。即,需要从保卫办出发,经过五餐,四餐,
需要驾车行走的最短总距离是:distance = 742。
2.3 计算结果和模型分析
dijkstra算法矩阵,用法看注释
function [ distance path] = Dijk( W,st,e )
%DIJK Summary of this function goes here
% W 权值矩阵 st 搜索的起点 e 搜索的终点
n=length(W);%节点数
D = W(st,:);
visit= ones(1,n); visit(st)=0;
parent = zeros(1,n);%记录每个节点的上一个节点
path =[];
for i=1:n-1
temp = [];
%从起点出发,找最短距离的下一个点,每次不会重复原来的轨迹,设置visit判断节点是否访问
for j=1:n
if visit(j)
temp =[temp D(j)];
else
temp =[temp inf];
end
end
[value,index] = min(temp);
visit(index) = 0;
%更新 如果经过index节点,从起点到每个节点的路径长度更小,则更新,记录前趋节点,方便后面回溯循迹
for k=1:n
if D(k)>D(index)+W(index,k)
D(k) = D(index)+W(index,k);
parent(k) = index;
end
end
end
distance = D(e);%最短距离
%回溯法 从尾部往前寻找搜索路径
t = e;
while t~=st && t>0
path =[t,path];
p=parent(t);t=p;
end
path =[st,path];%最短路径
end
举例说明Dijkstra算法用法:
假设目标是从37保卫办到21小北门,用Dijkstra算法计算出的最小距离和路线的Maltab命令是:
[distance,path] = Dijk(W,37,21),其中37可以换成任意的起点,21可以换成任意的终点数字,可以得到任意两点的最短距离和最优路线。
可以得到:
distance =
742
path =
37 9 8 16 15 21
计算结果表明算法计算结果和真实情况吻合,的确具有一定的科学性,并且我们随时可以根据道路的拥堵情况修改W道路权值矩阵的值,是最终结果满足改进后的情况
比如,今天大北门施工,小北门(21)和大北门(15)之间的权重可以设为Inf,
运行相同的代码[distance,path] = Dijk(W,37,21),
能得到新的结论如下:
distance =
767
path =
37 9 8 16 15 22 21
不但发现,程序的鲁棒性良好,而且容易根据现实情况进行改进。
本次为了简单起见,道路之间的权重只是节点之间的物理长度,还可以根据实际的情况,根据交通拥堵情况,或者节点之间的人流量,节点的火爆程度,出现意外导致节点之间交通不便等情况,适当地调整节点,从而得到更加精准的道路规划。
两者对应的实际路线图如下:白色两条线就是根据Dijistra算法得到的最优路线。
Floyd算法
function [D,path]=floyd(w)
%D R a
n=size(w,1);
%设初值
D=w;
path=zeros(n);
for i=1:n
for j=1:n
if D(i,j)~=inf
path(i,j)=j;
end
end
end
%迭代,更新D path
for k=1:n
for i=1:n
for j=1:n
if D(i,k)+D(k,j)
根据上述矩阵,我们很容易得到任意两点之间的最短距离和对应的路径。
同样的,举个例子,同样假设目标路径从37保卫办到21小北门,
查看D[37][21]=767,即两点之间发现最短距离和Dijkstra算法计算结果相同,均为767米。
再观察Path矩阵,
首先,
Path[37][21]=9,
Path[9][21]=8,
Path[8][21]=16,
Path[16][21]=15,
Path[15][21]=22,
Path[22][21]=21
也就是说,从37保卫办到21小北门的最短路径是
7->9->8->16->15->22->21
不出意外,果然和前面用Dijkstra算法计算出的最小距离和路线一摸一样,但是,这个方法的好处是,保卫办每个不需要每次都用Matlab等编程语言进行计算,可以随身或者在手机保存这两张矩阵,需要用到的情况下查表得到最优路线,免去重复计算,通过一次性的计算的结果得到某大学校区的任意两点之间的最短距离和路线规划。
展望和未来畅想
因为交通路网建立的过程中,没有考虑到每个公寓的居住人口,可以加入居住人口和日常出行,精确规划交通。
同时,因为每一个公寓的学生都是同一批年纪,可以加入他们的课程表信息,得到每日的人流量数据,得到学生交通流量的时间高峰和人流量高峰地段------校园宣传或者小广告派发能做到更加精准高效。
可以通过统计的方法,得到校区内的“事故高发区域”,认为设置权重,进一步对问题进行更精确的仿真,更符合真实情况的算法结论。
关于算法方面的优化,可以尝试运用神经网等现代算法对问题进行路线优化,模拟,从而得到对现实情况更加精准的仿真。
基于原问题模型假设的简化程度过高,还可以对问题进行进一步放宽假设,加强对现实情况的刻画程度,使预估效果更好,比如不把建筑区域抽象为质点,而是把建筑的面积和建筑之间的关系都考虑在一起。
除了考虑现有的汽车巡航路线,还可以考虑行人路线的道路规划,因为行人走的小路的最佳路线规划和汽车不一样,理应把校区内的路网分布更加复杂地设置为人行道排布的路网,从而得到针对行人的最短路线规划。
还能考虑校区内餐厅,快递,购物场所运动场所的的位置,考虑多目标规划下的最优路线规划,道路巡航规划。
推广意义
上述想法,只要在校内的路网能够加以实现,说明其他的路网全部都能采用相同的方法。
当进行城市交通路网规划的时候,可以根据车主的导航和日常统计大数据,实时反馈正常城市交通的轨道途径,为以后的交通出行规划做出更科学,更加合理的规划,建立更加合理的科学的城市交通规划实时调控机制。
通过社会调查和统计的方法,可以得到路网交通每日的人流量数据,得到学生交通流量的时间高峰和人流量高峰地段------校园宣传或者小广告派发能做到更加精准高效。
本问题的算法,很容易能够转移到其他编程语言去实现,比如在服务器上调用百度地图的API,根据Javascript改写的Dijkstra算法进行计算,不难得到任何地区想要求解的两点之间的道路规划。再有甚至,可以挂接在网站服务器上面,建立一个实时的Web应用,方便任何访问此网站的人员使用。
Floyd算法就更有推广价值了,只要以此计算得到D矩阵和Path矩阵,就能把矩阵打印出来,每次需要得到路线的时候就查表分析,短时间内计算出结果,摆脱对计算机和网络的依赖,轻松得到想要的结果。
最近在学习张淞的Haskell ,就拿函数式编程为例试试看:
import Data.List (transpose,minimumBy)
import Data.Ord (comparing)
type Distance = Double
type Name = String
type Direction = String
type Weight = (Distance, Direction)
zipD :: [Name] -> [[String]]
zipD ns = [[(start++"->"++des)| des <- ns ]|start <- ns]
zipW :: [[Distance]] -> [Name] -> [[Weight]]
zipW ds ns = [zip d n | (d, n) <- zip ds (zipD ns)]
tuplePlus :: Weight -> Weight -> Weight
tuplePlus (d1,n1) (d2,n2) = (d1+d2,n1++destination)
where (from,destination) = break (=='-') n2
type RouteMap = [[Weight]]
step ::RouteMap -> RouteMap -> RouteMap
step a b = [[minimumBy (comparing fst) $ zipWith tuplePlus ar bc | bc <- transpose b]|ar<-a]
infixl 5 |*|
(|*|) :: Num a => [[a]] -> [[a]] -> [[a]]
(|*|) a b = [[ sum $ zipWith (*) ar bc | bc <- transpose b ] | ar <- a]
iteration :: Int -> (a -> a) -> a -> a
iteration 0 f x = x
iteration n f x = iteration (n-1) f (f x)
steps :: Int -> RouteMap -> RouteMap
steps n route = iteration n (step route) route
fix f x = if dss == dss' then x else fix f x'
where
x' = f x
dss = [fst $ unzip ds|ds<-x']
dss' = [fst $ unzip ds|ds<-x ]
path :: [[Distance]] -> [Name] -> RouteMap
path dis ns = fix (step route) route
where route = zipW dis ns
infinity :: Fractional a => a
infinity = 1/0
i = infinity
graph:: [[Distance]]
graph=[[0,148,174,86,i,i,i,i,i,i,i,i,i,i,1144,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,317,i,i],[148,0,i,i,88,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[174,88,0,90,i,i,54,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[86,i,90,0,141,i,i,i,138,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,141,0,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,136,i],
[i,i,i,i,i,0,106,73,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,54,i,i,106,0,i,111,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,i,i,73,i,0,125,i,i,i,i,i,i,225,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,138,i,i,111,125,0,i,61,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,157,i],
[i,i,i,i,i,i,i,i,i,0,171,i,i,i,i,i,68,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,61,171,0,160,i,121,i,i,i,167,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,160,0,98,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,94,i],
[i,i,i,i,i,i,i,i,i,i,i,98,0,76,i,i,i,i,i,87,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,121,i,76,0,i,i,i,i,79,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[1144,i,i,i,i,i,i,i,i,i,i,i,i,i,0,56,i,i,i,i,i,156,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,225,i,i,i,i,i,i,56,0,85,i,i,i,i,i,207,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,68,i,i,i,i,i,85,0,96,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,167,i,i,i,i,i,96,0,64,i,i,i,i,147,147,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,79,i,i,i,64,0,83,i,i,i,i,i,192,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,87,i,i,i,i,i,83,0,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,113,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,207,i,i,i,i,0,48,i,i,i,i,i,i,i,i,i,i,251,i,785,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,156,i,i,i,i,i,48,0,58,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,58,0,288,245,i,i,i,92,i,i,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,147,i,i,i,i,288,0,48,i,i,i,i,i,i,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,245,48,0,92,i,i,i,119,i,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,192,i,i,i,i,i,92,0,88,i,i,i,138,i,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,88,0,75,i,i,i,116,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,75,0,i,i,i,i,i,i,i,199,i,68],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,92,i,i,i,i,i,0,213,i,i,i,156,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,119,i,i,i,213,0,115,i,i,i,137,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,138,i,i,i,115,0,74,i,i,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,116,i,i,i,74,0,i,i,i,i,i,70],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,251,i,i,i,i,i,i,i,i,i,i,i,0,120,i,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,156,i,i,i,120,0,190,i,i,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,785,i,i,i,i,i,i,i,i,137,i,i,i,190,0,1049,i,i],
[1317,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,113,i,i,i,i,i,i,i,199,i,i,i,i,i,i,1049,0,i,i],
[i,i,i,i,136,i,i,i,157,i,i,94,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,0,i],
[i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,i,68,i,i,i,70,i,i,i,i,i,0]]
names = ["A","B","C","D","E","F","G","H","I","J","K","L","M","N","O","P","Q","R","S","T","U","V","W","X","Y","Z","AA","AB","AC","AD","AE","AF","AG","AH","AI","AJ","AK","AL"]
PS:
想尝试跑跑看的人可以粘贴这个权值矩阵,没心情可以不看,这个没什么技术难度,就是太大了。
W=[0 148 174 86 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 1144 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 1317 Inf Inf
148 0 Inf Inf 88 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
174 88 0 90 Inf Inf 54 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
86 Inf 90 0 141 Inf Inf Inf 138 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf 141 0 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 136 Inf
Inf Inf Inf Inf Inf 0 106 73 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf 54 Inf Inf 106 0 Inf 111 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf 73 Inf 0 125 Inf Inf Inf Inf Inf Inf 225 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf 138 Inf Inf 111 125 0 Inf 61 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 157 Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf 0 171 Inf Inf Inf Inf Inf 68 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf 61 171 0 160 Inf 121 Inf Inf Inf 167 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 160 0 98 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 94 Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 98 0 76 Inf Inf Inf Inf Inf 87 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 121 Inf 76 0 Inf Inf Inf Inf 79 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
1144 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 0 56 Inf Inf Inf Inf Inf 156 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf 225 Inf Inf Inf Inf Inf Inf 56 0 85 Inf Inf Inf Inf Inf 207 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf 68 Inf Inf Inf Inf Inf 85 0 96 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 167 Inf Inf Inf Inf Inf 96 0 64 Inf Inf Inf Inf 147 147 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 79 Inf Inf Inf 64 0 83 Inf Inf Inf Inf Inf 192 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 87 Inf Inf Inf Inf Inf 83 0 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 113 Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 207 Inf Inf Inf Inf 0 48 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 251 Inf 785 Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 156 Inf Inf Inf Inf Inf 48 0 58 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 58 0 288 245 Inf Inf Inf 92 Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 147 Inf Inf Inf Inf 288 0 48 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 245 48 0 92 Inf Inf Inf 119 Inf Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 192 Inf Inf Inf Inf Inf 92 0 88 Inf Inf Inf 138 Inf Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 88 0 75 Inf Inf Inf 116 Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 75 0 Inf Inf Inf Inf Inf Inf Inf 199 Inf 68
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 92 Inf Inf Inf Inf Inf 0 213 Inf Inf Inf 156 Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 119 Inf Inf Inf 213 0 115 Inf Inf Inf 137 Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 138 Inf Inf Inf 115 0 74 Inf Inf Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 116 Inf Inf Inf 74 0 Inf Inf Inf Inf Inf 70
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 251 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 0 120 Inf Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 156 Inf Inf Inf 120 0 190 Inf Inf Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 785 Inf Inf Inf Inf Inf Inf Inf Inf 137 Inf Inf Inf 190 0 1049 Inf Inf
1317 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 113 Inf Inf Inf Inf Inf Inf Inf 199 Inf Inf Inf Inf Inf Inf 1049 0 Inf Inf
Inf Inf Inf Inf 136 Inf Inf Inf 157 Inf Inf 94 Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 0 Inf
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf 68 Inf Inf Inf 70 Inf Inf Inf Inf Inf 0];