Generative Adversarial Networks（生成对抗网络GAN，DCGAN）

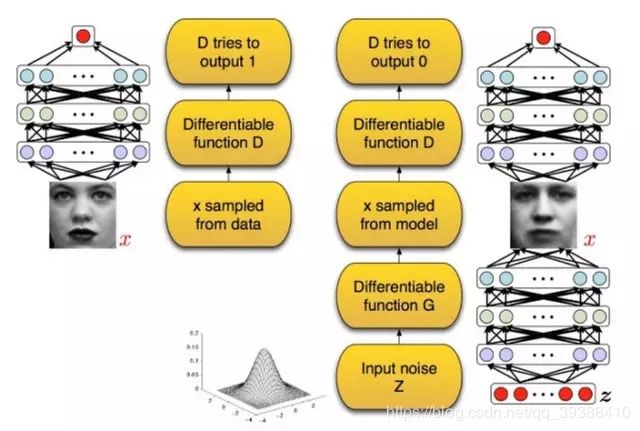
Generative Adversarial Networks
GAN的想法很简单，一言以蔽之：以假乱真。

（同样能做到相同效果的生成式模型有变分自编码等，而生成式模型的有点主要在于1.它能够有效的表征高维数据分布2.能够强化学习的辅助手段，更有效的表征state状态3.适用与半监督模型，即在无标签数据中也能训练模型给出输出。）
（GAN相比其他生成式模型的优点在于限制少、性能高。如不需要mcmc的适用分布，不需要VAE的变分界限。）

Generative（生成）：GAN实际上可以看作是一个生成数据的工具。目标就是通过学习让自身生成更加真实的数据。
Adversarial （对抗）：既然能够以假乱真，对抗的自然就是识别真假的警察了。

变分自编码VAE中有Encoder和Decoder，而GAN 也主要包括了两个部分：

• 生成器（Generator ）：生成器努力使生成的图像更加真实，以骗过判别器。
• 判别器（Discriminator） ：判别器则需要努力对图片进行真假判别，以识别出真假。

在整个训练过程中，捕获数据分布的生成器G和估计概率的判别器D通过这种不断地对抗最后达到一个动态平衡：即生成器生成的图像十分的接近真实图像的分布，从而造成判别器识别不出真假图像只能瞎猜（判断图片真假为0.5的抛硬币预测），达到以假乱真的目的。真实训练模型如下：

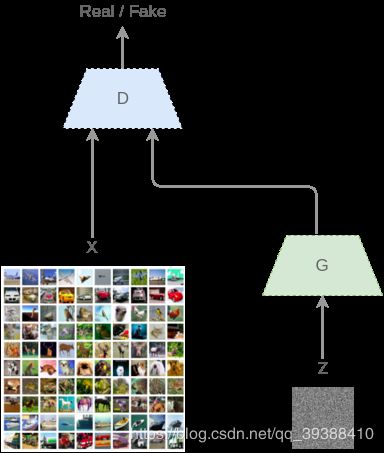
输入一个初始噪声z，然后通过生成器G得到一个伪造的数据G(z)。然后从真实数据集中取一部分即是真实的数据x，将两者混合后丢到判别器D，由判别器做这些图像是真（1）或假（0）的二分类，得到概率D(x)，最后计算出loss并回传。根据交叉熵损失此时的损失价值函数 V(D,G) 应该是：

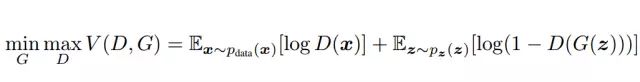
其中真实数据的x服从$P_{data}$分布，$P_z(z)$是噪声z的分布。G(z) 将z映射到数据空间去拟合真实图像的分布，而D(x)得到真实数据的概率。为了更好的学习到生成器在数据 x 上的分布P，训练时自然使D判断x是从P中取出的期望E最大化，同时最小化伪造的概率 $log(1-D(G(z)))$ 而训练了 G。

但但但！！是什么时候 D 能使 V(D,G) 取最大值？G 能 V(D,G) 取最小值？最优化的点在哪里？P的先验分布是什么？而D和V又是什么样子的函数或者网络？应该如何去学习？一定能收敛吗？

参拜原文： https://arxiv.org/pdf/1406.2661.pdf
原文用了大量的数学推导证明了：

• 最优生成器G值存在唯一解，且该唯一解满足 $P_G=P_{data}$ ,即生成的图像分布和原数据的分布近似的时候。即使用来判别两者分布相近的KL散度的参数 $\theta$ 最优即可。（JS散度优化了KL的不对称性，效果更好了）
• 最优判别器D满足条件，$D(x)=P_{data}/(P_{data}+P_G)$时，V（D，G）可取唯一的极大值。结合最优G的分布近似条件，可得此时值为50%，意味着分类器已经完全被迷惑了。
• P的先验分布并不需要知道，目标是使G逼近D就可以了。
• 只要有足够的训练数据和正确的环境，训练过程一定会收敛到最优。
• 能用SGD求解。
• 由x和z的分布都不知道，也就不能直接求出V的两个期望E，所以对于这种不知道的隐变量分布，老方法：采样吧！所以整个V可以近似变为：

$$V=\frac{1}{m}\sum _{i=1}^{m}logD(x^i)+\frac{1}{m}\sum _{i=1}^{m}log(1-D(G(z^i)))$$

实际训练使用梯度下降法，对D和G交替做优化，步骤为：

• 从随机噪声分布$P_z$中选出一些样本{$z^{(1)},z^{(2)},...z^{(m)}$}。
• 从训练数据x中选出同样m个的真实样本{$x^{(1)},x^{(2)},...x^{(m)}$}。
• 设判别器D的参数为 ${\theta }_d$，求出V关于参数的梯度，对${\theta }_d$更新时加上该梯度
• 设生成器G的参数为 ${\theta }_g$，同样求出V关于参数的梯度，对${\theta }_g$更新时减去该梯度

损失函数的变种

• LSGAN 将生成样本和真是样本分别编码为 a=-1，b=c=1，并使用平方误差代替了 GAN 的逻辑损失 。这样可以解决一部分训练不稳定和生成图像质量差的问题，但平方误差对离群点的过度惩罚，可能会导致过度模仿真实样本，降低生成结果的多样性。
• f-GAN用了不同的一组散度来衡量真假差（卡方散度，KL，逆KL，JS等等）

DCGAN
Deep Convolutional Generative Adversarial Networks，即深度卷积生成对抗网络。它利用了GAN的思想，专门用来“伪造”图像。判别器D是一个卷积网络，将输入的混合图片变成卷积特征然后通过 Logistic 函数，就得到了表示图像真或假的概率表示。而生成器G的卷积如下图所示：

生成器G的输入是一个为100 维的噪声向量z 。首先通过一个全连接层reshape为4x4x1024的向量，然后再使用几层转置卷积Deconv层做上采样，并且逐渐减少通道数，最后得到的输出64x64x3的“伪造”图片。

反卷积（Deconvolution）
反卷积也称转置卷积，实际上叫转置卷积会更加的合理。它的目的是将一个特征向量不断的放大变成所需要的尺寸，如把100维的噪声向量变成64x64x3大小的图片。

对于普通卷积操作如上图，那么记输入矩阵x为4X4的16维向量，而y是2X2共4维的输出向量，那么其实从 16维到4维的 卷积运算可表示为y = Cx，其中的C为4X16的矩阵如下：

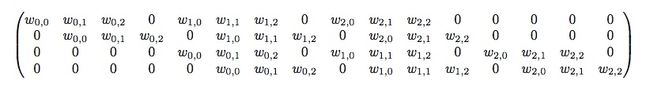
那么如果想要将图像放大，即需要从4维到16维，根据矩阵乘法，其实就只需要左乘$C^T$即可，这也就是转置卷积。
而直观上的理解，在乘$C^T$的时候w的对应位置同样会有大量的0，于是需要在周遭加入0的填充。

另外当stride不为1的时候，转置卷积的卷积核需要变成一个带“洞”的卷积，即微步卷积（fractional stride convolution）。为了完成步长为2，所以必须要带洞的原因是为了使卷积核以更小的步伐移动，以便使计算次数变多，反卷积得到的图也就越大（步长越大，卷积后会越小，反卷积需要越大）。

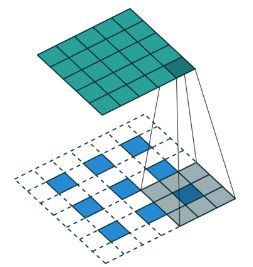
另外DCGAN与普通GAN不同的思想就是：在它的卷积中是直接用带步长的卷积代替池化，使用BN帮助收敛，G用ReLU（最后一层是tanh，以便图像的像素变成255之内），D用Leaky ReLU，优化函数是Adam。其他的与GAN一致，tf实现的关键代码如下：

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import os

#判别器D
X = tf.placeholder(tf.float32, shape=[None, 784])

D_W1 = tf.Variable(variable_init([784, 128]))
D_b1 = tf.Variable(tf.zeros(shape=[128]))
D_W2 = tf.Variable(variable_init([128, 1]))
D_b2 = tf.Variable(tf.zeros(shape=[1]))
theta_D = [D_W1, D_W2, D_b1, D_b2]

#生成器G
Z = tf.placeholder(tf.float32, shape=[None, 100])#100维的噪声向量

G_W1 = tf.Variable(variable_init([100, 128]))
G_b1 = tf.Variable(tf.zeros(shape=[128]))
G_W2 = tf.Variable(variable_init([128, 784]))
G_b2 = tf.Variable(tf.zeros(shape=[784]))
theta_G = [G_W1, G_W2, G_b1, G_b2]

def generator(z):#生成器
    #第一层先计算 y=z*G_W1+G_b1,然后投入激活函数计算G_h1=ReLU（y）,G_h1 为第二次层神经网络的输出激活值
    G_h1 = tf.nn.relu(tf.matmul(z, G_W1) + G_b1)
    
    #以下两个语句计算第二层传播到第三层的激活结果，第三层的激活结果是含有784个元素的向量，该向量转化28×28就可以表示图像
    G_log_prob = tf.matmul(G_h1, G_W2) + G_b2
    G_prob = tf.nn.sigmoid(G_log_prob)
    return G_prob
  
def discriminator(x):#判别器
    #计算D_h1=ReLU（x*D_W1+D_b1）,该层的输入为含784个元素的向量
    D_h1 = tf.nn.relu(tf.matmul(x, D_W1) + D_b1)
    
    #判别输入的图像到底是真（=1）还是假（=0）
    D_logit = tf.matmul(D_h1, D_W2) + D_b2
    D_prob = tf.nn.sigmoid(D_logit)
    
    return D_prob, D_logit

#损失函数：
G_sample = generator(Z)#噪音z
D_real, D_logit_real = discriminator(X)#分别判断其真伪
D_fake, D_logit_fake = discriminator(G_sample)

D_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit_real, labels=tf.ones_like(D_logit_real)))
D_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit_fake, labels=tf.zeros_like(D_logit_fake)))
D_loss = D_loss_real + D_loss_fake#加和两部分
G_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit_fake, labels=tf.ones_like(D_logit_fake)))

D_solver = tf.train.AdamOptimizer().minimize(D_loss, var_list=theta_D)
G_solver = tf.train.AdamOptimizer().minimize(G_loss, var_list=theta_G)

另外用keras的搭建也很直观，尝试完成和VAE一样生成MINIST的手写数字也很成功。

#生成模型
def generator_model():
    model = Sequential()
    model.add(Dense(input_dim=100, output_dim=1024))
    model.add(Activation('tanh'))
    model.add(Dense(128*7*7))
    model.add(BatchNormalization())
    model.add(Activation('tanh'))
    model.add(Reshape((7, 7, 128), input_shape=(128*7*7,)))
    model.add(UpSampling2D(size=(2, 2)))#上采样
    model.add(Conv2D(64, (5, 5), padding='same'))
    model.add(Activation('tanh'))
    model.add(UpSampling2D(size=(2, 2)))
    model.add(Conv2D(1, (5, 5), padding='same'))
    model.add(Activation('tanh'))
    return model

#判别模型
def discriminator_model():
    model = Sequential()
    model.add(
            Conv2D(64, (5, 5),
            padding='same',
            input_shape=(28, 28, 1))
            )
    model.add(Activation('tanh'))
    model.add(MaxPooling2D(pool_size=(2, 2)))
    model.add(Conv2D(128, (5, 5)))
    model.add(Activation('tanh'))
    model.add(MaxPooling2D(pool_size=(2, 2)))
    model.add(Flatten())
    model.add(Dense(1024))
    model.add(Activation('tanh'))
    model.add(Dense(1))
    model.add(Activation('sigmoid'))#Sigmoid输入类别
    return model

完整的细节源代码逐行中文注释：https://github.com/nakaizura/Source-Code-Notebook/tree/master/DCGAN

其中训练过程如下：

可以看到从一个噪音的初始值不断的生成了更好的“伪造”图片。

GAN训练的模式崩溃问题(Mode Collapse)
对于生成模型很重要的两点是：生成器所生成样本的质量和样本多样性。
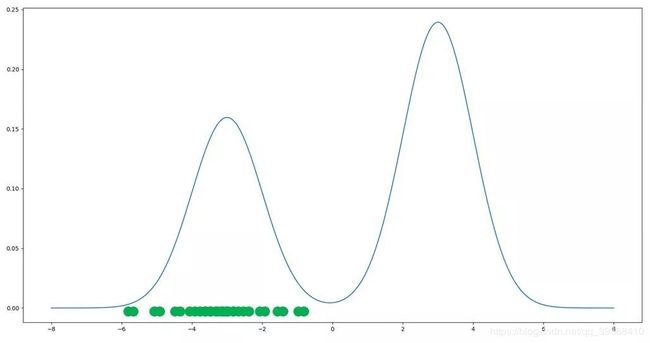
根据数据的流形分布定律，自然界中同一类别的高维数据，往往集中在某个低维流形附近，所以生成器最理想的情况是：将输入的噪声都映射到训练数据所在的流形上，并且与训练数据的概率分布对应。但是如下图，原本应该只生成绿色的点（即符合在两个分布峰下的数据分布），却产生了一些质量不高的红色样本点。

但出现少部分红色的点也在模型训练的可接受范围内，只要样本的整体质量不错就可以了。而关于另一个点–样本的多样性，即模式崩溃问题，生成器所产生样本大量重复类似，基本上只聚集在了一个峰之下。（好比生成手写数字只能够很好的生成数字“1”，但是不能生成其他的任何数字）

这种问题的产生要归功于 GAN的参数优化问题并不是一个凸优化问题，存在许多局部纳什均衡状态，所以如果GAN进入某个纳什均衡状态，即使损失函数表现为收敛，它仍然不是我们想要的结果。那么解决方案只有：

那么如何使生成器能够“及时发现问题”，自动调整权值，将生成样本分散到整个训练数据的流形上呢？改变目标函数。
判别器的目标函数仍然为$${\theta }_D=argmaxf({\theta }_G,{\theta }_D)$$但改变生成器的目标函数，其中K为梯度下降连续更新K次。$${\theta }_G=argminf({\theta }_G,{\theta }_D^K({\theta }_G,{\theta }_D))$$
即生成器在更新时，不仅仅考虑当前生成器的状态，还会额外考虑以当前状态为起始点，判别器更新K次后的状态，综合两个信息做出最优解，从而避免了短视行为。

DRAGAN
DRAGAN是另一种解决模式崩溃的方法，以上通过更改损失函数，但明显提高了计算量。不过观察得知，如果GAN一旦出现模式崩溃问题，判别器在训练样本附近更新参数时，其梯度值非常大，故DRAGAN的解决方法是：对判别器，在训练样本附近施加梯度惩罚项。

$$E_{x\sim p_{data},ϵ\sim N_d(0,cI)}[||{▽}_{x}D(x+ϵ)||-1{]}^2$$
这种方式试图在训练样本附近构建线性函数，因为线性函数为凸函数具有全局最优解。

MADGAN
既然单个生成器会造成模式崩溃问题，那么就构造多个生成器吧。即在MADGAN（multi-agent diverse）中，用k个初始值不同的生成器和1个判别器来解决问题，其中判别器的输出softmax需要变成k+1维，即前k维是判断样本来自于那个生成器，k+1是标签，标记是否从第i个生成器获得。判别器的目标函数为交叉熵：
$$ma{x}_{{\theta }_d}{E}_{x\sim P_{data}}log[D_{k+1}(x)]+\sum _{i=1}^k{E}_{x_i\sim p_{g_i}}log[D_i(x_i)]$$
直观上会使x尽量靠近某个生成器，而不是其他生成器。而生成器的目标函数为：
$$mi{n}_{{\theta }_{g_i}}{E}_{x\sim P_x}log[1-D_{k+1}(G_i(z))]$$
不同的生成器相互排斥以产生不一样的样本。

训练技巧
GAN两大问题：难收敛，模式崩溃。

• Feature matching：最小化判别器出来的特征和真实的特征，而不是预测出标签
• 标签平滑：把1变成0.8-1的随机数
• 谱归一化：对每一层都加入Lipschitz约束

GAN系列总结
关于损失函数的度量问题,LSGAN,f-GAN
模式崩溃问题,DRAGAN,MADGAN
收敛不稳定问题,WGAN,WGAN-GP
对偶学习，源域迁移问题,CycleGAN
条件控制问题,cGAN,IcGAN
图像质量（分辨率）提升,SAGAN,CoGAN
生成的准确性与多样性,IS,FID