强化学习（Policy Gradient，Actor Critic）

强化学习是通过奖惩的反馈来不断学习的，在Q-Learning，Sarsa和DQN中，都是学习到了价值函数或对价值函数的近似，然后根据价值来选择策略（如选择最大价值的动作），所以这一类也被称为Value Based Model。但是这种处理方式有几处瓶颈：

• 处理连续动作效果差。对于高维度或连续状态空间，使用Value Based通过得到价值函数再制定策略，需要比较所有action的价值大小，此时选出最大价值行为会十分艰难。
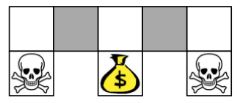
• 受制环境而无法最优。空间观测局限，无法准备的描述场景。如上图想要获得金币、躲避骷髅，但是仔细观察这个环境，灰色的两个格子其实是无法区分的，即状态重名（Aliased），这种环境一致但结果截然相反会极大的影响到学习过程。
• 不能解决随机策略问题。随机策略往往可能是最优的，但Value Based无法学习到随机策略。比如石头剪刀布，如果一直坚持某个确定性策略，怎么可能不输？显然最好的策略就是随机选择以得到最大可能的总体奖励。

那么不用Value Based？但如果不用，又如何通过价值函数来确定“好”的策略呢？
直接学习策略吧！即Policy Based Model。即不通过奖励，直接基于策略来学习。即先预测动作，通过reward来评价当前动作的“好”与“坏”，如果好，这个动作下次被选中的概率就增加

策略梯度（Policy Gradient）
首先明确目标仍然是为了使奖励价值最大，那么就可以设计一个目标函数来衡量策略的好坏，然后优化策略的参数，最后使得目标函数值最大化就完成目标了。

近似表达策略本身为$${\pi }_{\theta }(s,a)=P(a|s,\theta )\approx \pi (a|s)$$
然后针对不同应用场景，会有三种目标函数的设计选择：

• Start value。对于能获得完整回合的场景。即从某状态s1开始直到结束后所能获得的总奖励。那么最大化这个值就好：$$J_1(\theta )=V^{{\pi }_{\theta }}(s_1)={\mathbb{E}}_{{\pi }_{\theta }}(v_1)$$

• Average Value。对于连续环境的场景。由于不存在开始状态s，那么就只好对每个可能的出现状态，计算从它开始一直持续与环境交互下去能够得到的总奖励，再求对各状态的概率分布和，即$$J_{avV}(\theta )=\sum _s{d}^{{\pi }_{\theta }}(s)V^{{\pi }_{\theta }}(s)$$其中$d^{{\pi }_{\theta }}(s)$是在当前策略下马尔科夫链的关于状态的一个静态分布，描述状态的不断交互。同样最大化这个式子就好。

• Average reward per time-step。在某段确定的时间内，按步长估计评价奖励。即某个时间步长里，得到所有状态的发生的概率及其采取所有可能行为能够得到的即时奖励，再按概率求和得到$$J_{avR}(\theta )==\sum _s{d}^{{\pi }_{\theta }}(s)\sum _a{\pi }_{\theta }(s,a)R_s^a$$

其实这三个式子都尝试描述了在某一状态的能获得的价值，但是是直接通过策略来得到的价值。即想要求出在状态s时，所有动作a出现的概率函数，以尽可能的获得更多的奖励。（比如通过神经网络近似的动作输出可以是40%向上行动，60%向下行动等）。

如何求解目标函数梯度？

• 直接求导再梯度上升求解最大值。但很多目标损失函数很难求导。
• 有限差分法来估计。
  
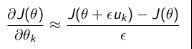
  不要求策略函数可微分，适用于任意策略，但有噪声，且大多数时候不高效。
• 蒙特卡罗策略梯度。算法流程如下：
  
  实际上就是先采样，再计算序列在 t 时刻的状态价值，并用于更新策略$\pi$的参数。$$\theta =\theta +\alpha {\nabla }_{\theta }log{\pi }_{\theta }(s_t,a_t)v_t$$

得到了目标函数梯度的式子，如何对策略函数进行设计？
即解决${\nabla }_{\theta }log{\pi }_{\theta }(S_t,A)$动作分值函数的问题：

• 离散：根据Softmax概率进行选择。
• 连续：根据高斯分布随机产生。

策略函数的目的就是为了选择动作，然后通过选择动作的标准再给MC进行采样（所以需要回合更新），再计算梯度进行学习。从梯度更新的式子中可以理解到，由于reward会评价所选择的动作，所以整个学习的模式就变成了，动作价值高的就多采样，价值小的就少采样。策略乘奖励价值的梯度会通过如神经网络反向传递，进而又影响动作的分布，调整它输出的动作概率。这也就是完整的基于策略的强化学习方法了。利用参数化的策略函数，通过调整这些参数得到策略，使尽可能得到最大奖励。（设计一个目标损失函数，梯度上升优化参数以最大化奖励）

Actor Critic
同样的梯度策略使用了mc做估计，虽然无偏但是噪声大，利用采样间的结果进行计算会使模型不太稳定，那么有没有更好的估值方法？
估值？Q-Learning这样的不就可以来估值嘛？可以直接用这样的估计的值来指导梯度计算吗？（换个角度，Q-Learning不好的地方是连续动作或者高维度动作的选择，通过结合的方式而让它可以更轻松的基于策略来选择动作也是一大提升）
Policy Based +Value Based=Actor Critic

“演员-评论”（Actor Critic），相当于演员在演戏actor的同时有评论家critic不断的指点打分，继而使演员演得越来越好，这里充当评论家的便是价值函数的估计了。Actor基于概率选行为，critic基于actor的行为评判得分reward（同样可以用新旧state做均方误差更新自己的参数），然后actor再根据critic的评分修改选行为的概率。

评估点
能作为评估点的地方有很多。作为指导研究的评论家来说，可以说这个actor歌喉不佳，也可以说他舞姿不美，更可以指责他演戏太烂，甚至私生活…即要类似策略评估一样，需要有一个确切的评估点。

• 基于状态价值。向着状态价值大的方向学习。
  $$\theta =\theta +\alpha {\nabla }_{\theta }log{\pi }_{\theta }(s_t,a_t)V(s,w)$$
• 基于动作价值。向着动作价值大的方向学习。
  $$\theta =\theta +\alpha {\nabla }_{\theta }log{\pi }_{\theta }(s_t,a_t)Q(s,a,w)$$
• 基于TD误差。
  $$\theta =\theta +\alpha {\nabla }_{\theta }log{\pi }_{\theta }(s_t,a_t)(R_{t+1}+\gamma V(S_{t+1})-V(S_t))$$

结合Q-Learning做价值函数计算的Actor Critic算法流程如下：

• 初始化所有的状态s和动作对应的价值Q，然后在每一轮迭代中，先初始化第一个状态S，并得到特征向量$\varphi (S)$（这里用DQN近似模拟的方式）。
• 然后将$\varphi (S)$输入Actor网络中，估计得到一个动作A和执行动作的新状态S’和奖励R。
• Critic网络中输入新旧状态的$\varphi (S)$，$\varphi (S^{\prime })$，能得到两者的价值函数$V(S)，V(S’)$。
• 然后均方误差$\sum (R+\gamma V(S’)-V(S,w){)}^2$调整Critic网络的更新。
• 然后TD策略评估$\theta =\theta +\alpha {\nabla }_{\theta }log{\pi }_{\theta }(s_t,a_t)(R_{t+1}+\gamma V(S_{t+1})-V(S_t))$更新Actor网络。

AC的Tensorflow实现

代码来自github。实现的是gym里面的CartPole-v0游戏，即控制小车的移动使杆子能够立起来。所以每个状态都有四个参数：Cart Position（车的位置）、Cart Velocity（车的速度）、Pole Position（杆子的位置）和Pole Velocity at Tip（杆的倾斜角度）。动作只有向左和向右移动。

import numpy as np
import tensorflow as tf
import gym
import pandas as pd

MAX_EPISODE = 500 #最大回合数
RENDER = False  # 不直接显示
DISPLAY_REWARD_THRESHOLD = 10  #如果reward大于10时才显示
MAX_EP_STEPS = 2000  # 每个回合最大的时间步
GAMMA = 0.9  # td损失的价值折现
LR_A = 0.001  # actor的学习率
LR_C = 0.001  # critic的学习率

#actor
class Actor(object):
    def __init__(self, sess, n_features, n_actions, lr=0.001):
        self.sess = sess

        self.s = tf.placeholder(tf.float32, [1, n_features], "state") #状态
        self.a = tf.placeholder(tf.int32, None, "action") #动作
        self.q = tf.placeholder(tf.float32, None, "q")  # TD损失

        with tf.variable_scope('Actor'):
            l1 = tf.layers.dense(
                inputs=self.s,
                units=20,  # 隐藏层数量
                activation=tf.nn.relu,
                kernel_initializer=tf.random_normal_initializer(0., .1),  # 随机初始化权重
                bias_initializer=tf.constant_initializer(0.1),  # 初始化偏差
                name='l1'
            )

            self.acts_prob = tf.layers.dense(
                inputs=l1,
                units=n_actions,  # output units
                activation=tf.nn.softmax,  # softmax来得到动作出现的概率
                kernel_initializer=tf.random_normal_initializer(0., .1), 
                bias_initializer=tf.constant_initializer(0.1), 
                name='acts_prob'
            )

        with tf.variable_scope('exp_v'):
            log_prob = tf.log(self.acts_prob[0, self.a])
            self.exp_v = tf.reduce_mean(log_prob * self.q)  # td损失的均方误差指导参数更新

        with tf.variable_scope('train'):
            self.train_op = tf.train.AdamOptimizer(lr).minimize(-self.exp_v)  #最小“-”，即最大话损失函数

    def learn(self, s, a, q):td损失q来自 Critic, 用于评价Actor 
        s = s[np.newaxis, :]
        feed_dict = {self.s: s, self.a: a, self.q: q}
        _, exp_v = self.sess.run([self.train_op, self.exp_v], feed_dict)
        return exp_v

    def choose_action(self, s):
        s = s[np.newaxis, :]
        probs = self.sess.run(self.acts_prob, {self.s: s})  #得到所有action的概率
        return np.random.choice(np.arange(probs.shape[1]), p=probs.ravel()) #根据概率来选 action
        
#critic
class Critic(object):
    def __init__(self, sess, n_features,n_actions, lr=0.01):
        self.sess = sess

        self.s = tf.placeholder(tf.float32, [None, n_features], "state")
        self.a = tf.placeholder(tf.int32,[None, 1],"action")
        self.r = tf.placeholder(tf.float32, None, 'r') #reward
        self.q_ = tf.placeholder(tf.float32,[None,1],'q_next')

        self.a_onehot = tf.one_hot(self.a, n_actions, dtype=tf.float32)
        self.a_onehot = tf.squeeze(self.a_onehot,axis=1)

        self.input = tf.concat([self.s,self.a_onehot],axis=1)

        with tf.variable_scope('Critic'):
            l1 = tf.layers.dense(
                inputs=self.input,
                units=20,  #隐藏层数目
                activation=tf.nn.relu,  
                kernel_initializer=tf.random_normal_initializer(0., .1),  
                bias_initializer=tf.constant_initializer(0.1), 
                name='l1'
            )

            self.q = tf.layers.dense(
                inputs=l1,
                units=1,  # 输出层为1
                activation=None,
                kernel_initializer=tf.random_normal_initializer(0., .1), 
                bias_initializer=tf.constant_initializer(0.1),  
                name='Q'
            )

        with tf.variable_scope('squared_TD_error'):
            self.td_error = self.r + GAMMA * self.q_ - self.q
            self.loss = tf.square(self.td_error)  # TD_error = (r+gamma*V_next) - V_eval
        with tf.variable_scope('train'):
            self.train_op = tf.train.AdamOptimizer(lr).minimize(self.loss)

    def learn(self, s, a, r, s_):
        s, s_ = s[np.newaxis, :], s_[np.newaxis, :] #新旧状态的向量
        next_a = [[i] for i in range(N_A)] #下一个动作
        s_ = np.tile(s_,[N_A,1])
        q_ = self.sess.run(self.q, {self.s: s_,self.a:next_a})
        q_ = np.max(q_,axis=0,keepdims=True)
        q, _ = self.sess.run([self.q, self.train_op],
                                    {self.s: s, self.q_: q_, self.r: r,self.a:[[a]]})
        return q


env = gym.make('CartPole-v0') #载入CartPole-v0的游戏
env.seed(1)  # 可再生的随机种子
env = env.unwrapped # 取消限制

#得到环境的观察空间维度（4）和动作维度（2）
N_F = env.observation_space.shape[0]
N_A = env.action_space.n

sess = tf.Session()

#初始化两个网络
actor = Actor(sess, n_features=N_F, n_actions=N_A, lr=LR_A)
critic = Critic(sess, n_features=N_F,n_actions=N_A,lr=LR_C)

sess.run(tf.global_variables_initializer())

res = []
for i_episode in range(MAX_EPISODE):#开始循环
    s = env.reset()#刷新界面
    t = 0
    track_r = [] #每回合的所有奖励
    while True:
        if RENDER: env.render()

        a = actor.choose_action(s) #根据s选动作

        s_, r, done, info = env.step(a) #执行动作得到新的s‘，奖励r和是否终止的信息

        if done: r = -20 #结束游戏的惩罚

        track_r.append(r)

        q = critic.learn(s, a,r, s_)  # critic进行学习，gradient = grad[r + gamma * V(s_) - V(s)] 
        actor.learn(s, a, q)  # actor进行学习， true_gradient = grad[logPi(s,a) * td_error]

        s = s_ #下一状态
        t += 1 #时间步

        if done or t >= MAX_EP_STEPS: #没有结束，时间步也没有超过
            ep_rs_sum = sum(track_r)

            if 'running_reward' not in globals():
                running_reward = ep_rs_sum
            else:
                running_reward = running_reward * 0.95 + ep_rs_sum * 0.05
            if running_reward > DISPLAY_REWARD_THRESHOLD: RENDER = True  #大于值了再显示
            print("episode:", i_episode, "  reward:", int(running_reward))
            res.append([i_episode,running_reward])
            break

pd.DataFrame(res,columns=['episode','ac_reward']).to_csv('../ac_reward.csv') #记录训练过程