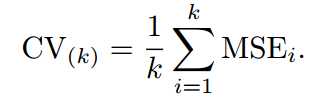[交叉验证]机器学习中分类器的选择

我的机器学习教程「美团」算法工程师带你入门机器学习   已经开始更新了，欢迎大家订阅~

任何关于算法、编程、AI行业知识或博客内容的问题，可以随时扫码关注公众号「图灵的猫」，加入”学习小组“，沙雕博主在线答疑~此外，公众号内还有更多AI、算法、编程和大数据知识分享，以及免费的SSR节点和学习资料。其他平台（知乎/B站）也是同名「图灵的猫」，不要迷路哦~

 

 

 

 

 

在机器学习中，分类器作用是在标记好类别的训练数据基础上判断一个新的观察样本所属的类别。分类器依据学习的方式可以分为非监督学习和监督学习。非监督学习顾名思义指的是给予分类器学习的样本但没有相对应类别标签，主要是寻找未标记数据中的隐藏结构。，监督学习通过标记的训练数据推断出分类函数，分类函数可以用来将新样本映射到对应的标签。在监督学习方式中，每个训练样本包括训练样本的特征和相对应的标签。监督学习的流程包括确定训练样本的类型、收集训练样本集、确定学习函数的输入特征表示、确定学习函数的结构和对应的学习算法、完成整个训练模块设计、评估分类器的正确率。这一节的目的是分类器的选取。可以依据下面四个要点来选择合适的分类器。

1. 泛化能力和拟合之间的权衡

过拟合评估的是分类器在训练样本上的性能。如果一个分类器在训练样本上的正确率很高，说明分类器能够很好地拟合训练数据。但是一个很好的拟合训练数据的分类器就存在着很大的偏置，所以在测试数据上不一定能够得到好的效果。如果一个分类器在训练数据上能够得到很好效果但是在测试数据上效果下降严重，说明分类器过拟合了训练数据。从另一个方面分析，若分类器在测试数据上能够取得好效果，那么说明分类器的泛化能力强。分类器的泛化和拟合是一个此消彼长的过程，泛化能力强的分类器拟合能力一般很弱，另外则反之。所以分类器需要在泛化能力和拟合能力间取得平衡。

2. 分类函数的复杂度和训练数据的大小

训练数据的大小对于分类器的选择也是至关重要的，如果是一个简单的分类问题，那么拟合能力强泛化能力弱的分类器就可以通过很小的一部分训练数据来得到。反之，如果是一个复杂的分类问题，那么分类器学习就需要大量的训练数据和泛化能力强的学习算法。一个好的分类器应该能够根据问题的复杂度和训练数据的大小自动地调整拟合能力和泛化能力之间的平衡。

3. 输入的特征空间的维数

如果输入特征空间的向量维数很高的话，就会造成分类问题变得复杂，即使最后的分类函数仅仅就靠几个特征来决定的。这是因为过高的特征维数会混淆学习算法并且导致分类器的泛化能力过强，而泛化能力过强会使得分类器变化太大，性能下降。因此，一般高维特征向量输入的分类器都需要调节参数使其泛化能力较弱而拟合能力强。另外在实验中，也可以通过从输入数据中去除不相干的特征或者降低特征维数来提高分类器的性能。

4. 输入的特征向量之间的均一性和相互之间的关系

如果特征向量包含多种类型的数据（如离散，连续），许多分类器如SVM，线性回归，逻辑回归就不适用。这些分类器要求输入的特征必须是数字而且要归一化到相似的范围内如 之间。而像K最近邻算法和高斯核的SVM这些使用距离函数的分类器对于数据的均一性更加敏感。但是另一种分类器决策树却能够处理这些不均一的数据。如果有多个输入特征向量，每个特征向量之间相互独立，即当前特征向量的分类器输出仅仅和当前的特征向量输入有关，那么最好选择那些基于线性函数和距离函数的分类器如线性回归、SVM、朴素贝叶斯等。反之，如果特征向量之间存在复杂的相互关系，那么决策树和神经网络更加适合于这类问题。

接下来确定经验风险的最小化值

交叉验证(Cross-validation)

1.The Validation Set Approach

第一种是最简单的，也是很容易就想到的。我们可以把整个数据集分成两部分，一部分用于训练，一部分用于验证，这也就是我们经常提到的训练集（training set）和测试集（test set）。

 

例如，如上图所示，我们可以将蓝色部分的数据作为训练集（包含7、22、13等数据），将右侧的数据作为测试集（包含91等），这样通过在蓝色的训练集上训练模型，在测试集上观察不同模型不同参数对应的MSE的大小，就可以合适选择模型和参数了。

 

不过，这个简单的方法存在两个弊端。

1.最终模型与参数的选取将极大程度依赖于你对训练集和测试集的划分方法。什么意思呢？我们再看一张图：

右边是十种不同的训练集和测试集划分方法得到的test MSE，可以看到，在不同的划分方法下，test MSE的变动是很大的，而且对应的最优degree也不一样。所以如果我们的训练集和测试集的划分方法不够好，很有可能无法选择到最好的模型与参数。

2.该方法只用了部分数据进行模型的训练

我们都知道，当用于模型训练的数据量越大时，训练出来的模型通常效果会越好。所以训练集和测试集的划分意味着我们无法充分利用我们手头已有的数据，所以得到的模型效果也会受到一定的影响。

基于这样的背景，有人就提出了Cross-Validation方法，也就是交叉验证。

2.Cross-Validation

2.1 LOOCV

首先，我们先介绍LOOCV方法，即（Leave-one-out cross-validation）。像Test set approach一样，LOOCV方法也包含将数据集分为训练集和测试集这一步骤。但是不同的是，我们现在只用一个数据作为测试集，其他的数据都作为训练集，并将此步骤重复N次（N为数据集的数据数量）。

 

如上图所示，假设我们现在有n个数据组成的数据集，那么LOOCV的方法就是每次取出一个数据作为测试集的唯一元素，而其他n-1个数据都作为训练集用于训练模型和调参。结果就是我们最终训练了n个模型，每次都能得到一个MSE。而计算最终test MSE则就是将这n个MSE取平均。

 

 

比起test set approach，LOOCV有很多优点。首先它不受测试集合训练集划分方法的影响，因为每一个数据都单独的做过测试集。同时，其用了n-1个数据训练模型，也几乎用到了所有的数据，保证了模型的bias更小。不过LOOCV的缺点也很明显，那就是计算量过于大，是test set approach耗时的n-1倍。

 

为了解决计算成本太大的弊端，又有人提供了下面的式子，使得LOOCV计算成本和只训练一个模型一样快。

 

其中表示第i个拟合值，而则表示leverage。关于的计算方法详见线性回归的部分（以后会涉及）。

 

2.2 K-fold Cross Validation

另外一种折中的办法叫做K折交叉验证，和LOOCV的不同在于，我们每次的测试集将不再只包含一个数据，而是多个，具体数目将根据K的选取决定。比如，如果K=5，那么我们利用五折交叉验证的步骤就是：

1.将所有数据集分成5份

2.不重复地每次取其中一份做测试集，用其他四份做训练集训练模型，之后计算该模型在测试集上的

3.将5次的取平均得到最后的MSE

 

不难理解，其实LOOCV是一种特殊的K-fold Cross Validation（K=N）。再来看一组图：

 

 

每一幅图种蓝色表示的真实的test MSE，而黑色虚线和橙线则分贝表示的是LOOCV方法和10-fold CV方法得到的test MSE。我们可以看到事实上LOOCV和10-fold CV对test MSE的估计是很相似的，但是相比LOOCV，10-fold CV的计算成本却小了很多，耗时更少。

 

2.3 Bias-Variance Trade-Off for k-Fold Cross-Validation

最后，我们要说说K的选取。事实上，和开头给出的文章里的部分内容一样，K的选取是一个Bias和Variance的trade-off。

K越大，每次投入的训练集的数据越多，模型的Bias越小。但是K越大，又意味着每一次选取的训练集之前的相关性越大（考虑最极端的例子，当k=N，也就是在LOOCV里，每次都训练数据几乎是一样的）。而这种大相关性会导致最终的test error具有更大的Variance。

一般来说，根据经验我们一般选择k=5或10。

2.4 Cross-Validation on Classification Problems

上面我们讲的都是回归问题，所以用MSE来衡量test error。如果是分类问题，那么我们可以用以下式子来衡量Cross-Validation的test error：

 

其中Erri表示的是第i个模型在第i组测试集上的分类错误的个数。