数字签名原理及其应用详解

序言

---

签名的作用无非就是证明某个文件上的内容确实是我写的/我认同的，别人不能冒充我的签名（不可伪造），我也不能否认上面的签名是我的（不可抵赖）。

我们知道，手写签名之所以不能伪造，是因为每一个人的笔迹都是独一无二的，即使模仿，也可以通过专家鉴定分别出来。而不可抵赖，是因为每个人的笔迹都有固定特征，这些特征是很难摆脱的。

正是这两点特性使得手写签名在日常生活中被广泛承认，比如签合同、借条等等。

而数字签名，它的作用跟手写签名其实是一样的，用来证明某个消息或者文件是本人发出/认同的。我国在2005年就已经施行《电子签名法》，确立了电子签名（包括但不限于数字签名）的法律效力。

那么数字签名又是靠什么保证不可伪造和不可抵赖两个特性呢？

答案是利用公钥加密系统。常用的签名算法有

• RSA，基于大整数分解问题
• DSA，基于离散对数问题
• ECDSA，属于DSA的一个变种，基于椭圆曲线上的离散对数问题

其中RSA是实现数字签名最简单的公钥加密方法。

RSA签名

---

RSA是一个非常神奇的加密算法，它具有一个离散对数和椭圆曲线加密都没有的特性：

既可以用公钥加密然后私钥解密，也可以用私钥加密然后公钥解密（对称性）。

公钥加密然后私钥解密，可以用于通信中拥有公钥的一方向拥有私钥的另一方传递机密信息，不被第三方窃听。
那么私钥加密然后公钥解密是用在什么场合呢？就是数字签名。

因为RSA中的每一个公钥都有唯一的私钥与之对应，任一公钥只能解开对应私钥加密的内容。换句话说，其它私钥加密的内容，这个公钥是解不开的。

这样，如果你生成了一对RSA密钥，你把公钥公布出去，并告诉全世界人这个公钥是你的。之后你只要在发送的消息，比如“123456”，后面加上用私钥加密过的密文，其他人拿公钥解密，看解密得到的内容是不是“123456”就可以知道这个“123456”是不是你发的。

其他人因为没有对应的私钥，所以没法生成公钥可以解密的密文，所以是不可伪造的。
又因为公钥对应的私钥只有一个，所以只要能成功解密，那么发消息的一定是你，不会是其他人，所以是不可抵赖的。

当然，在数字签名的过程中，我们不需要对“123456”保密，所以加密、解密这样的名词在这个场景中并不准确，用签名和解签会更合适。

实际应用中，由于直接对原消息进行签名有安全性问题，而且原消息往往比较大，直接使用RSA算法进行签名速度会比较慢，所以我们一般对消息计算其摘要（使用SHA-256等安全的摘要算法），然后对摘要进行签名。只要使用的摘要算法是安全的（MD5、SHA-1已经不安全了），那么这种方式的数字签名就是安全的。

一个具体的RSA签名过程如下：

1. 小明对外发布公钥，并声明对应的私钥在自己手上
2. 小明对消息M计算摘要，得到摘要D
3. 小明使用私钥对D进行签名，得到签名S
4. 将M和S一起发送出去

验证过程如下：

1. 接收者首先对M使用跟小明一样的摘要算法计算摘要，得到D
2. 使用小明公钥对S进行解签，得到D’
3. 如果D和D’相同，那么证明M确实是小明发出的，并且没有被篡改过

应用

---

手写签名可以用来签合同，那么数字签名可以用来干什么呢？

网站认证

首先最常见的用处就是用来认证一个网站的身份。
比如我打开百度，百度是怎么保证显示在我眼前的网页就一定是百度生成的，不是其他人修改的呢？就是借助数字签名来实现的。

用IE浏览器打开百度，点击地址栏旁边的小锁，再点击查看证书，就可以看到百度主页的数字签名证书了。所谓证书，其实是对公钥的封装，在公钥的基础上添加了诸如颁发者之类的信息。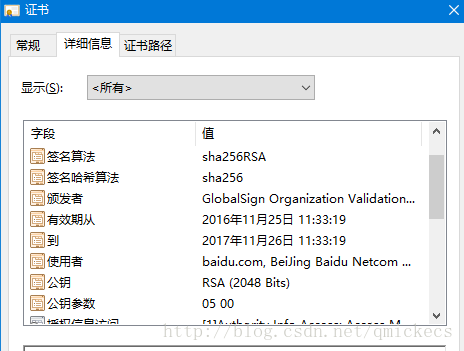

“签名算法”一栏可以看到，它使用的是sha256RSA，也就是使用SHA-256计算摘要，然后使用RSA对摘要进行签名。而在“公钥”一栏则保存着该证书的“本体”，用于验证签名的RSA公钥。

代码签名

而除此之外，还有个地方我们经常碰到数字签名的——代码签名。

如果Windows上的可执行程序程序来源于正规公司，那么通常它会有代码签名，用于确保其来源可靠且未被篡改。以QQ为例，它的数字签名是这样的。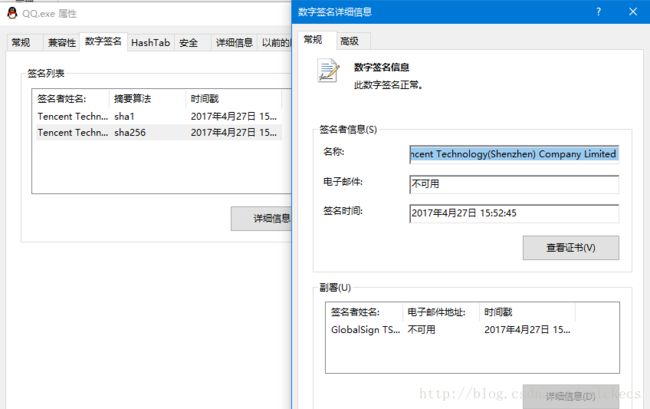

如果某个程序没有数字签名，那么它的安全性往往就没有保证，如果它有数字签名，但是显示“此数字前面无效”，那么这个程序要么被篡改了要么损坏了，不管哪种可能都不应该尝试执行它。

实际上，验证数字签名并不需要我们手动去查看，如果你没有关闭Windows的UAC（用户账户控制）功能，那么你在执行任何程序的时候系统都会自动验证其签名，如果是签名有效的程序，那么弹出来的UAC对话框是蓝色或者灰色的，如果没有签名，那么会是醒目黄色的。而如果签名被阻止，则会显示红色并且不允许执行。

但是数字签名不是万能的。事实上不管是浏览器的数字签名还是代码的数字签名，都依赖于系统或者浏览器内置的根证书，如果电脑本身已经中毒或者被入侵，那么这些根证书可以被轻易添加或者修改，这时的数字签名的安全性可以说是荡然无存了。

即使是正常签名的软件，也不能保证发行公司不耍流氓，很多流氓软件都是由一些不知名的小公司搞出来的；或者某些小公司篡改知名软件，加入自己的代码，然后用自己的私钥进行签名，这些数字签名也都是有效的，但是我相信你不会想运行这些软件的。如果对安全性要求比较高，可以手动或者借助工具吊销那些不太安全的根证书，具体方法已经超出本文讨论范畴，读者可以自行寻找。

比特币

比特币是一种完全匿名的数字货币，它的身份认证是基于ECDSA。比特币的账户地址就是对公钥计算摘要得到的，向全世界公布。而确认你是账户拥有者的唯一办法就是看你有没有账户对应的私钥。对于比特币中的任意一个交易记录，只有当其中付款方的签名是有效的，它才是有效的。如果账户私钥丢失，那么你将永远地失去里面的钱；一旦被黑客盗取，里面的钱就完全归黑客所有。

DSA

---

上面说到，RSA是数字签名最简单的算法，为了做对比，大家可以感受一下DSA是如何实现的。

• 参数生成：

  1. 选取素数q
  2. 选取素数p使得p-1是q的整数倍
  3. 随机选取小于p-1的整数h，计算g=h(p−1)/q
  4. 选取小于q的正整数x作为私钥
  5. 计算y=gxmodp 得到公钥

• 签名（其中H(M)是消息M的摘要）：

  1. 对每一条消息随机生成大于1小于q的整数k
  2. 计算r=(gkmodp)modq，如果r=0，重新回到步骤1
  3. 计算s=k−1(H(m)+xr)modq，如果s=0，重新回到步骤1
  4. 得到签名(r, s)

• 验证：

  1. 计算w=s−1modq
  2. 计算u1=H(m)⋅wmodq
  3. 计算u2=r⋅wmodq
  4. 计算v=(gu1yu2modp)modq
  5. 如果v=r，则签名有效，否则无效

可以看到DSA过程明显要比RSA签名复杂不少，除非亲自动手去推导它的正确性，不然很难直观地感受为什么这样是可行的。

参考文献

---

Microsoft TechNet: Digital Signatures
Wikipedia: Digital Signature Algorithm
Wikipedia: Elliptic Curve Digital Signature Algorithm