【详解】半平面交算法入门详解(计算几何)

半平面交

简介

博客背景

笔者在学习半平面交时，网上找入门博客资源甚少，且大部分难以理解，故在稍稍入门了半平面交后，写此博客，希望能对大家有所帮助。若有错误，麻烦指出。

半平面交是什么？

我们知道一条直线可以把平面分为两部分，其中一半的平面就叫半平面。
那半平面交，就是多个半平面的相交部分。我们在学习线性规划时就有用过。

半平面交有什么用？

1.求解一个区域，可以看到给定图形的各个角落。(多边形的核)
2.求可以放进多边形的圆的最大半径。

求解半平面交的步骤(S&I算法 O(nlogn))

我们试着来解决 “求解一个区域，可以看到给定图形的各个角落。”
为了叙述方便，我们把这个区域叫做多边形的核。

1.选取一个正方向。(一般为逆时针)

我们用这个一个不规则图形举例子。

首先我们选逆时针方向做为有向线段。

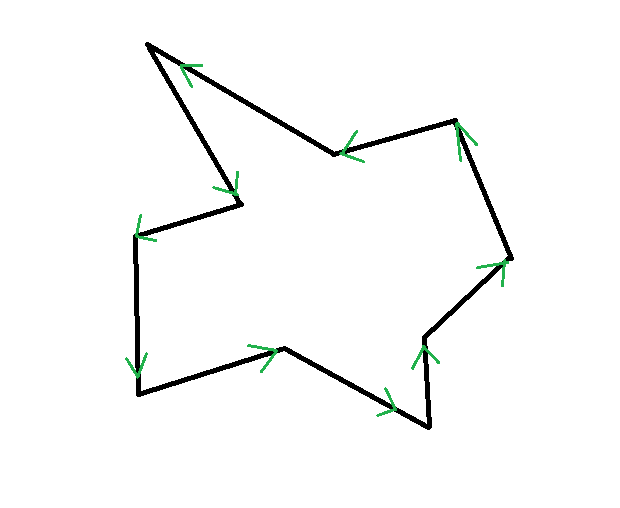
这样选取的好处是，保证核在有向线段的左边。

2.把有向线段通过极角排序(与 $x$ 轴的夹角)(-180°,180°]

排序结果如下所示。

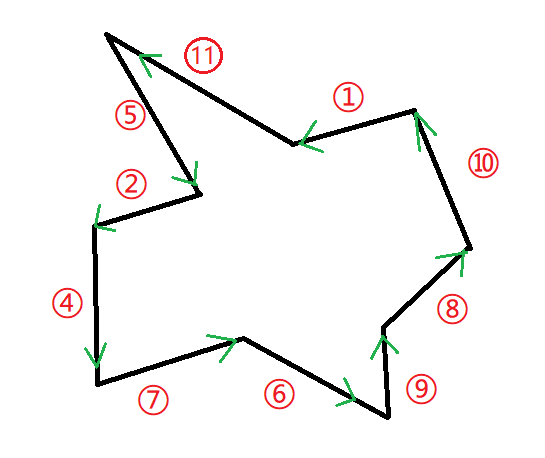
按照极角排序的原因是写代码方便，排序之后的线段是有序的，可以在双端队列里进行操作。(下面会再解释)。

3.按顺序遍历每条线段，取左边区域，删右边区域

我们用这个 S&I 算法求解半平面交时，用的是删减法，首先我们假设全部平面都是半平面交，然后不断加入直线，不断删去右边区域，保留左边区域。最后剩下的区域就是需要求的半平面交。

1.全部平面都是半平面交。

2.加入第一条直线，保留左边区域，删除右边区域。

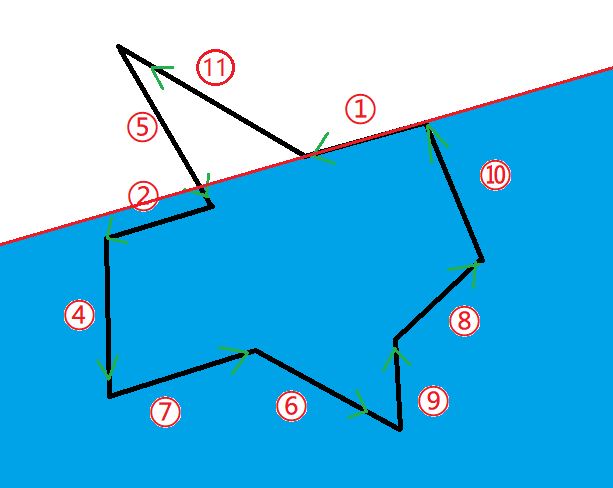
3.加入第二条线段，保留左边区域，删除右边区域。

4.依次加入3 - 10线段，保留左边区域，删除右边区域。

5.加入最后一条线段，保留左边区域，删除右边区域。

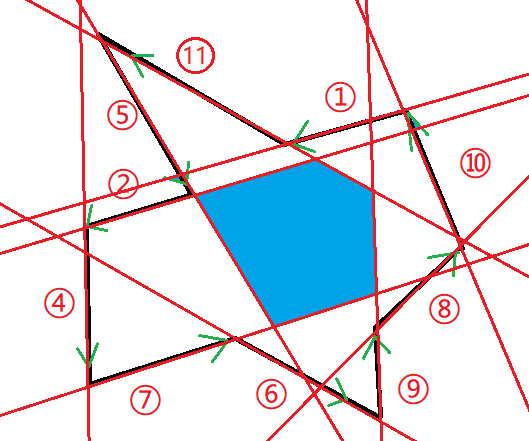
6.剩下的蓝色部分，就是多边形的和，也就是所有直线的半平面交，在蓝色区域的任何一点，都可以看到多边形的每一个角落。

7.这时我们得到的是围成这个蓝色区域的直线集合。

$L=\{2，5，7，9，11\}$ ，如果至少有三条边，就说明该多边形有核(三条以上时，核为全部直线围成的凸包。)如果要求面积，我们可以将直线的交点求出来，然后再用叉积求凸包面积。

4.如果题目要求求面积。

我们可以发现求出来的直线的集合是有序的 $L=\{2，5，7，9，11\}$，这些直线刚好是逆时针围着这个半平面交。(这就是按极角排序的好处)。如果要求面积，我们可以把所有$L[i]$ 和 $L[i+1]$ 的交点求出来，然后用叉乘求凸包面积。

5.总结

总体而言，求半平面交其实就是维护线段的集合 $L$，遍历每一条线段，判断这条线段加入后对于半平面交的影响，然后在集合 $L$ 中剔除掉对半平面交没有决定作用的边，留下起决定作用的边。即最终目的是维护半平面交的线段集合 $L$。

6.算法优化

1.同极角时，排序后可以去掉右边的线段，保留左边的线段。

例如上述步骤 3-3 时，加入第二条线段。不难发现，当①号线段和②号线段的极角相同时，①号线段没有意义。因为①号线段在②号线段右边。因此在排序后，可以去掉没有意义的线段，即保留极角相同的情况下最左边的线段。

算法实现 $S\&I$算法 $O$($nlogn$)

算法流程

1.以逆时针为正方向，建边。(输入方向不确定时，可用叉乘求面积看正负得知输入的顺逆方向。)
2.对线段根据极角排序。
3.去除极角相同的情况下，位置在右边的边。
4.用双端队列储存线段集合 $L$，遍历所有线段。
5.判断该线段加入后对半平面交的影响，(对双端队列的头部和尾部进行判断，因为线段加入是有序的。)。
6.如果某条线段对于新的半平面交没有影响，则从队列中剔除掉。
7.最后剩下的线段集合 $L$，即使最后要求的半平面交。

疑问解答

1.为什么要用双端队列？

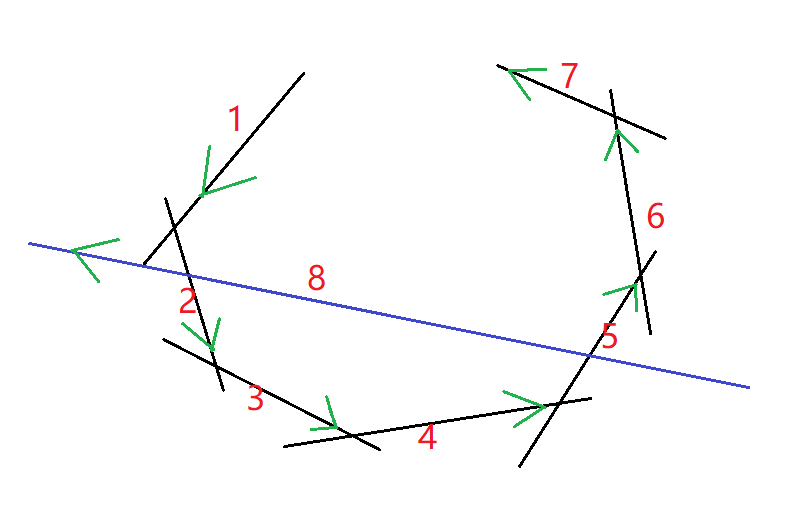
因为线段是按照极角排序的，所以可以形成环，如图，原来的线段集合为
$L=\{1，2，3，4，5，6，7\}$。现在我们想把线段 8 加入到线段集中，显然核的形成和线段1、6、7已经没有关系了，因此我们应该在队列的头部找到线段 1，把它删去，然后在队列的尾部找到线段6、7，然后删除掉。

2.线段这么才对半平面交没有影响？

在下图中，蓝色为当前半平面交。

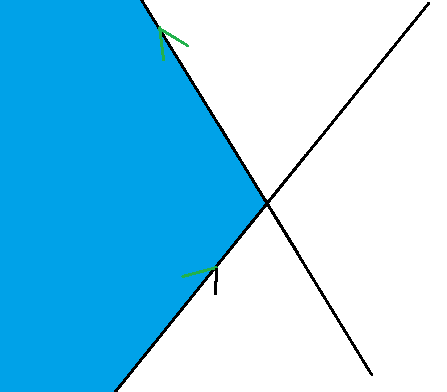
当我们加入红色线段时，半平面交产生了变化。

因为我们对线段进行了排序，所以加入的线段会比前面的更“陡”。显然，如果先前的两条线段的交点在当前加入线段的右侧，则较“陡”的那条线段就会无效。

代码实现

poj3335

#include 
#include 
#include 
#include 
#include 
using namespace std;
const int maxn = 1e3;
const double EPS = 1e-5;
int T, n;
typedef struct Grid {
  double x, y;
  Grid(double a = 0, double b = 0) {x = a, y = b;}
} Point, Vector;
Vector operator - (Point a, Point b) {return Vector(b.x - a.x, b.y - a.y);}
double operator ^ (Vector a, Vector b) {return a.x * b.y - a.y * b.x;}//叉乘
struct Line {
  Point s, e;
  Line() {}
  Line(Point a, Point b) {s = a, e = b;}
};
Point p[maxn];
Line L[maxn], que[maxn];

//得到极角角度
double getAngle(Vector a) {
  return atan2(a.y, a.x);
}

//得到极角角度
double getAngle(Line a) {
  return atan2(a.e.y - a.s.y, a.e.x - a.s.x);
}

//排序：极角小的排前面，极角相同时，最左边的排在最后面，以便去重
bool cmp(Line a, Line b) {
  Vector va = a.e - a.s, vb = b.e - b.s;
  double A =  getAngle(va), B = getAngle(vb);
  if (fabs(A - B) < EPS) return ((va) ^ (b.e - a.s)) >= 0;
  return A < B;
}

//得到两直线相交的交点
Point getIntersectPoint(Line a, Line b) {
  double a1 = a.s.y - a.e.y, b1 = a.e.x - a.s.x, c1 = a.s.x * a.e.y - a.e.x * a.s.y;
  double a2 = b.s.y - b.e.y, b2 = b.e.x - b.s.x, c2 = b.s.x * b.e.y - b.e.x * b.s.y;
  return Point((c1*b2-c2*b1)/(a2*b1-a1*b2), (a2*c1-a1*c2)/(a1*b2-a2*b1));
}

//判断 b,c 的交点是否在 a 的右边
bool onRight(Line a, Line b, Line c) {
  Point o = getIntersectPoint(b, c);
  if (((a.e - a.s) ^ (o - a.s)) < 0) return true;
  return false;
}

bool HalfPlaneIntersection() {
  sort(L, L + n, cmp);//排序
  int head = 0, tail = 0, cnt = 0;//模拟双端队列
  //去重，极角相同时取最后一个。
  for (int i = 0; i < n - 1; i++) {
    if (fabs(getAngle(L[i]) - getAngle(L[i + 1])) < EPS) {
      continue;
    }
    L[cnt++] = L[i];
  }
  L[cnt++] = L[n - 1];


  for (int i = 0; i < cnt; i++) {
    //判断新加入直线产生的影响
    while(tail - head > 1 && onRight(L[i], que[tail - 1], que[tail - 2])) tail--;
    while(tail - head > 1 && onRight(L[i], que[head], que[head + 1])) head++;
    que[tail++] = L[i];
  }
  //最后判断最先加入的直线和最后的直线的影响
  while(tail - head > 1 && onRight(que[head], que[tail - 1], que[tail - 2])) tail--;
  while(tail - head > 1 && onRight(que[tail - 1], que[head], que[head + 1])) head++;
  if (tail - head < 3) return false;
  return true;
}

//判断输入点的顺序，如果面积 <0，说明输入的点为逆时针，否则为顺时针
bool judge() {
  double ans = 0;
  for (int i = 1; i < n - 1; i++) {
    ans += ((p[i] - p[0]) ^ (p[i + 1] - p[0]));
  }
  return ans < 0;
}

int main()
{
  scanf("%d", &T);
  while (T--) {
    scanf("%d", &n);
    for (int i = n - 1; i >= 0; i--) {
      scanf("%lf %lf", &p[i].x, &p[i].y);
    }

    if (judge()) {//判断输入顺序，保证逆时针连边。
      for (int i = 0; i < n; i++) {
        L[i] = Line(p[(i + 1)%n], p[i]);
      }
    } else {
      for (int i = 0; i < n; i++) {
        L[i] = Line(p[i], p[(i + 1)%n]);
      }
    }

    if (HalfPlaneIntersection()) printf("YES\n");
    else printf("NO\n");
  }

  return 0;
}