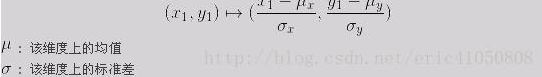（大数据分析学习）22 切比雪夫、曼哈顿、欧几里德、闵可夫斯基、马哈拉诺比斯距离解释收集

本文从公式上表述了欧几里得距离、曼哈顿距离、切比雪夫距离记忆闵可夫斯基距离之间的关系。收集整理的资料大多来自于书本和网络。

首先是书中的解释：

一般而言，定义一个距离函数 d(x,y), 需要满足下面几个准则：

1) d(x,x) = 0 // 到自己的距离为0 

2) d(x,y) >= 0 // 距离非负 

3) d(x,y) = d(y,x) // 对称性: 如果 A 到 B 距离是 a，那么 B 到 A 的距离也应该是 a 

4) d(x,k) d(k,y) >= d(x,y) // 三角形法则: (两边之和大于第三边)

 

切比雪夫距离：

Dis（A,B）=max(|XA−XB|,|YA−YB|)

Dis（A,B）=max(|XA−XB|,|YA−YB|)

曼哈顿距离：

Dis(A,B)=|XA−XB|+|YA−YB|

曼哈顿距离又称Manhattan distance，还见到过更加形象的，叫出租车距离的。具体贴一张图，应该就能明白。

上图摘自维基百科，红蓝黄皆为曼哈顿距离，绿色为欧式距离。

欧式距离：

欧式距离又称欧几里得距离或欧几里得度量（Euclidean Metric），以空间为基准的两点之间最短距离，与之后的切比雪夫距离的差别是，只算在空间下。

曼哈顿距离与切比雪夫距离：

两者的定义看上去好像毛线关系都没有，但实际上，这两种距离可以相互转化！

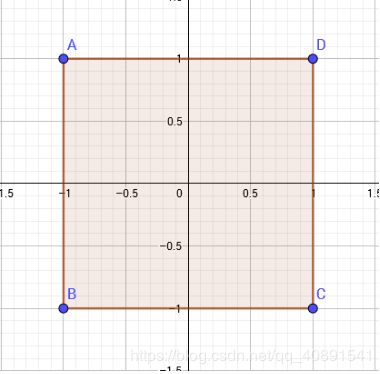
我们考虑最简单的情况，在一个二维坐标系中，设原点为(0,0)；

如果用曼哈顿距离表示，则与原点距离为1的点会构成一个边长为√2的正方形

如果用切比雪夫距离表示，则与原点距离为1的点会构成一个边长为2的正方形

仔细对比这两个图形，我们会发现这两个图形长得差不多，他们应该可以通过某种变换互相转化。

事实上,将一个点(x,y)的坐标变为(x+y,x−y)后,原坐标系中的曼哈顿距离=新坐标系中的切比雪夫距离。而将一个点(x,y)的坐标变为(x+y2,x−y2)后,原坐标系中的切比雪夫距离=新坐标系中的曼哈顿距离

 

或者使用公式：

去max的方法：max(X,Y)=(X+Y+|X−Y|)/2 

去绝对值的方法：|X−Y|=max(X−Y,Y−X)

由此来推导公式。

 

闵氏距离

闵可夫斯基距离（Minkowski distance）是衡量数值点之间距离的一种非常常见的方法，假设数值点 P 和 Q 坐标如下：

那么，闵可夫斯基距离定义为：

明氏距离又叫做明闵可夫斯基距离（Minkowski distance），根本不是种概念，或者可以说是以一种集合或者公式。

当纬度等于1时候，其公式等价于曼哈顿距离。

等于2时候，其公式等价于欧式距离。

当大于2到无穷大时候，其公式等价于切比雪夫距离。

 

注意，当 p < 1 时，闵可夫斯基距离不再符合三角形法则，举个例子：当 p < 1, (0,0) 到 (1,1) 的距离等于 (1 1)^{1/p} > 2, 而 (0,1) 到这两个点的距离都是 1。

闵可夫斯基距离比较直观，但是它与数据的分布无关，具有一定的局限性，如果 x 方向的幅值远远大于 y 方向的值，这个距离公式就会过度放大 x 维度的作用。所以，在计算距离之前，我们可能还需要对数据进行 z-transform 处理，即减去均值，除以标准差：

可以看到，上述处理开始体现数据的统计特性了。这种方法在假设数据各个维度不相关的情况下利用数据分布的特性计算出不同的距离。如果维度相互之间数据相关（例如：身高较高的信息很有可能会带来体重较重的信息，因为两者是有关联的），这时候就要用到马氏距离（Mahalanobis distance）了。

 

Mahalanobis Distance & Euclidean Distance

Definition

  马氏距离（Mahalanobis Distance）是由印度统计学家马哈拉诺比斯（P. C. Mahalanobis）提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的）并且是尺度无关的（scale-invariant），即独立于测量尺度。 

  对于一个均值为，协方差矩阵为的多变量，其马氏距离为： 

  如果是单位阵的时候，马氏距离简化为欧氏距离。 

 

Why is Mahalanobis distance?

  马氏距离有很多优点，马氏距离不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关；由标准化数据和中心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。 

  它的缺点是夸大了变化微小的变量的作用。

这个stackexchange问答很好的回答了马氏距离的解释： 

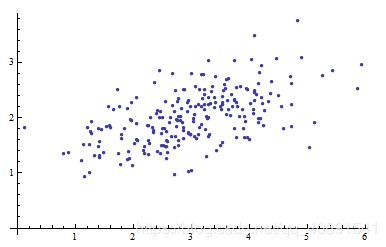
  下图是一个二元变量数据的散点图： 

  当我们将坐标轴拿掉，如下图，我们能做些什么呢？ 

  那就是根据数据本身的提示信息来引入新的坐标轴。

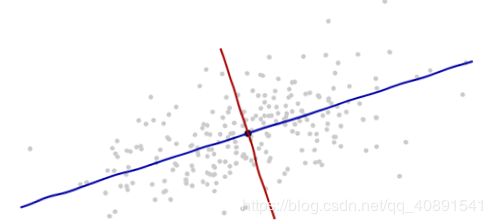
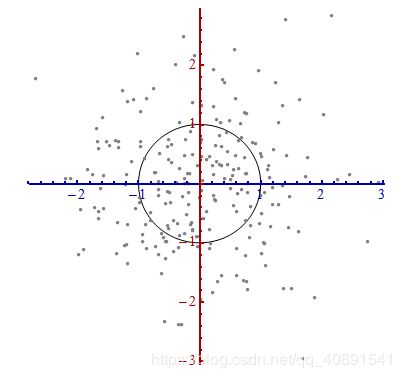
  坐标的原点在这些点的中央（根据点的平均值算得）。第一个坐标轴（下图中蓝色的线）沿着数据点的“脊椎”，并向两端延伸，定义为使得数据方差最大的方向。第二个坐标轴（下图红色的线）会与第一个坐标轴垂直并向两端延伸。如果数据的维度超过了两维，那就选择使得数据方差是第二个最大的方向，以此类推。 

  我们需要一个比例尺度。用数据沿着每一个坐标轴的标准差来定义一个单位长度。要记住68-95-99.7法则：大约2/3的点需要在离原点一个单位长度的范围内；大约95%的点需要在离原点两个单位的长度范围内；这会使得我们更紧盯着正确的单元。为了以示参考，如下图： 

  上图并不像是一个圆，对吧？那是因为这幅图是被扭曲的（图中，不同轴上的单位长度不一样）。因此，让我们重新沿着正确的方向画图——从左到右，从下到上（相当于旋转一下数据）。同时，并让每个轴方向上的单位长度相同，这样横坐标上一个单位的长度就与纵坐标上的单位长度相同。 

  这里发生了什么？我们让数据告诉我们怎样去从散点图中构建坐标系统，以便进行测量。这就是上面所要表达的内容。尽管在这样的过程中我们有几种选择（我们可以将两个坐标轴颠倒；在少数的几种情况下，数据的“脊椎”方向——主方向，并不是唯一的），但是这些在最后并不影响距离。 

 

Technical comments

  沿着新坐标轴的单位向量是协方差矩阵的特征向量。

  注意到没有变形的椭圆，变成圆形后沿着特征向量用标准差（协方差的平方根）将距离长度分割。用代表协方差函数，点之间的距离（Mahalanobis distance）就是之间以方差的平方根为单位长度所分割产生的长度：。对应的代数式是，。这个公式不管用什么基底表示向量以及矩阵时都成立。特别是，这个公式在原始的坐标系中对于Mahalanobis Distance的计算也正确。

  在最后一步中，坐标轴扩展的量是协方差矩阵的逆的特征值（平方根），同理的，坐标轴缩小的量是协方差矩阵的特征值。所以，点越分散，需要的将椭圆转成圆的缩小量就越多。

  尽管上述的操作可以用到任何数据上，但是对于多元正态分布的数据表现更好。在其他情况下，点的平均值或许不能很好的表示数据的中心，或者数据的“脊椎”（数据的大致趋势方向）不能用变量作为概率分布测度（using variance as a measure of spread）来准确的确定。

  原始坐标系的平移、旋转，以及坐标轴的伸缩一起形成了仿射变换（affine transformation）。除了最开始的平移之外，其余的变换都是基底变换，从原始的一个变为新的一个。

  对于多元正太分布，Mahalanobis 距离（已经变换到新的原点）出现在表达式中的位置，描述标准正太分布的概率密度。因此，在新的坐标系中，多元正态分布像是标准正太分布，当将变量投影到任何一条穿过原点的坐标轴上。特别是，在每一个新的坐标轴上，它就是标准正态分布。从这点出发来看，多元正态分布彼此之实质性的差异就在于它们的维度。注意，这里的维数可能，有时候会少于名义上的维数。 

 

 假设数据分布是一个二维的正椭圆，轴轴均值都为0，轴的方差为1000，轴的方差为1，考虑两个点到原点的距离，如果计算的是欧氏距离那么两者相等，但是仔细想一下，因为x轴的方差大，所以应该是更接近中心的点，也就是正态分布标准差的原则。这时候需要对轴进行缩放，对应的操作就是在协方差矩阵的对角上加上归一化的操作，使得方差变为1.

  假设数据分布是一个二维的椭圆，但是不是正的，比如椭圆最长的那条线是的，因为矩阵的对角只是对坐标轴的归一化，如果不把椭圆旋转回来，这种归一化是没有意义的，所以矩阵上的其他元素（非对角）派上用场了。如果椭圆不是正的，说明变量之间是有相关性的（x大y也大，或者负相关），加上协方差非对角元素的意义就是做旋转。

上图是，一个左下右上方向标准差为 3，正交方向标准差为 1 的多元高斯分布的样本点。由于 x 和 y 分量共变（即相关），x 与 y 的方差不能完全描述该分布；箭头的方向对应的协方差矩阵的特征向量，其长度为特征值的平方根。 

参考：

https://www.cnblogs.com/zwfymqz/p/8253530.html#_label3

https://blog.csdn.net/young951023/article/details/78171934

https://blogs.sas.com/content/iml/2012/02/15/what-is-mahalanobis-distance.html

http://blog.sina.com.cn/s/blog_ebbe6d790101e1e2.html

https://blog.csdn.net/Riven__/article/details/79847143

https://www.luogu.org/problemnew/show/P3964

《MATLAB数据分析与挖掘实战》