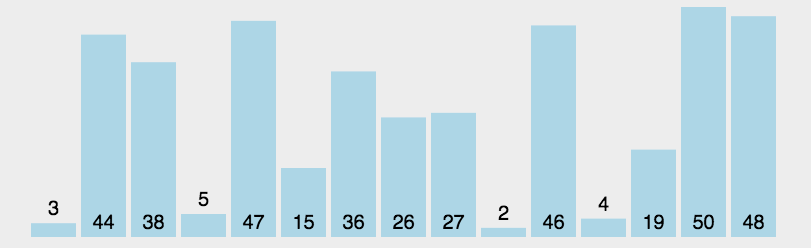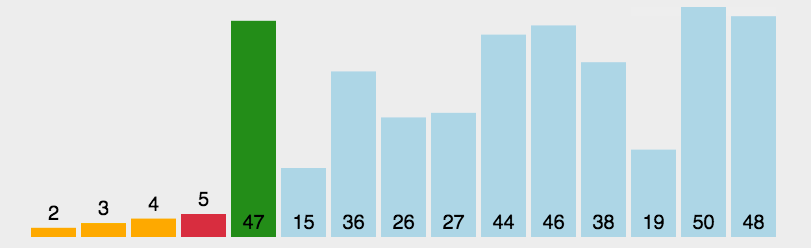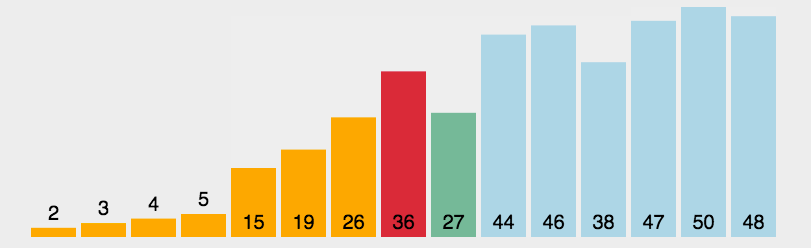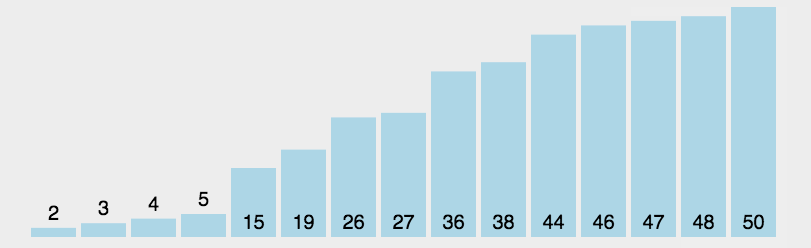
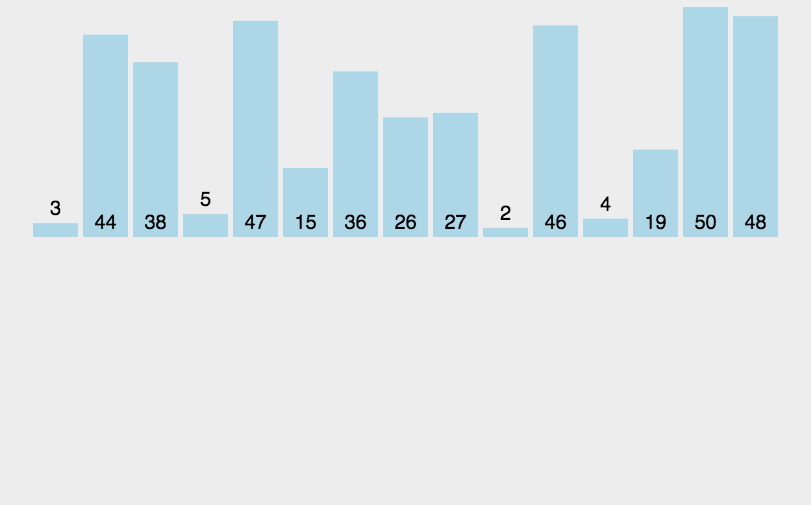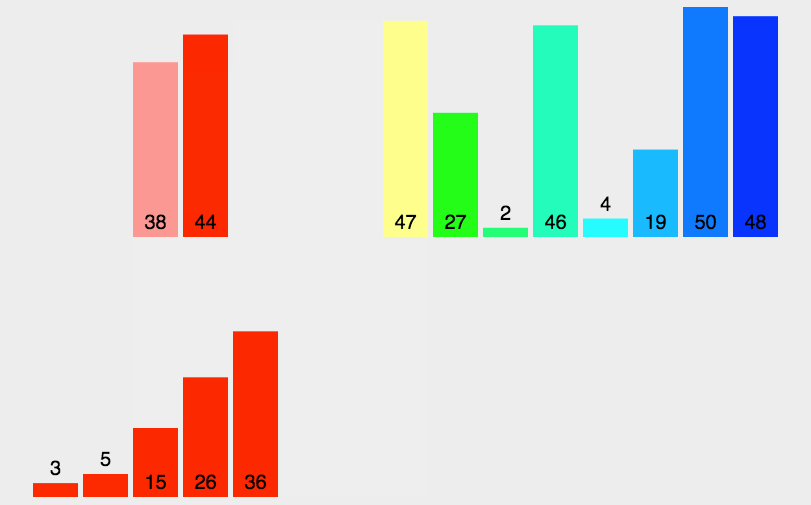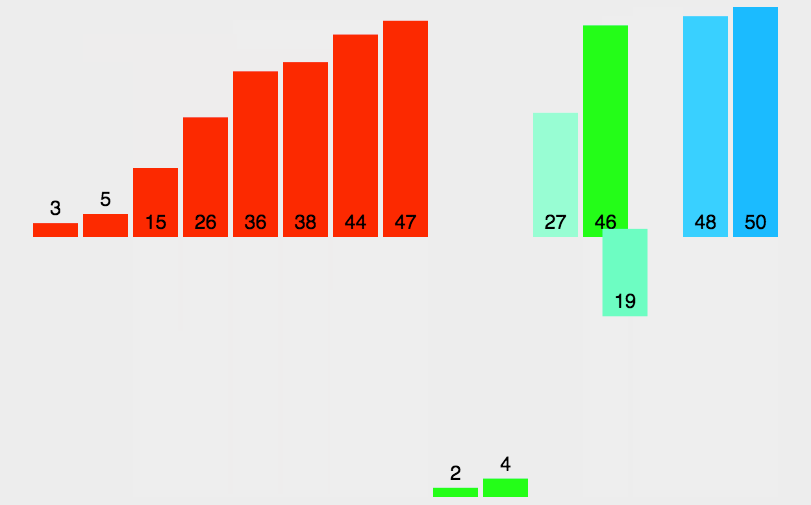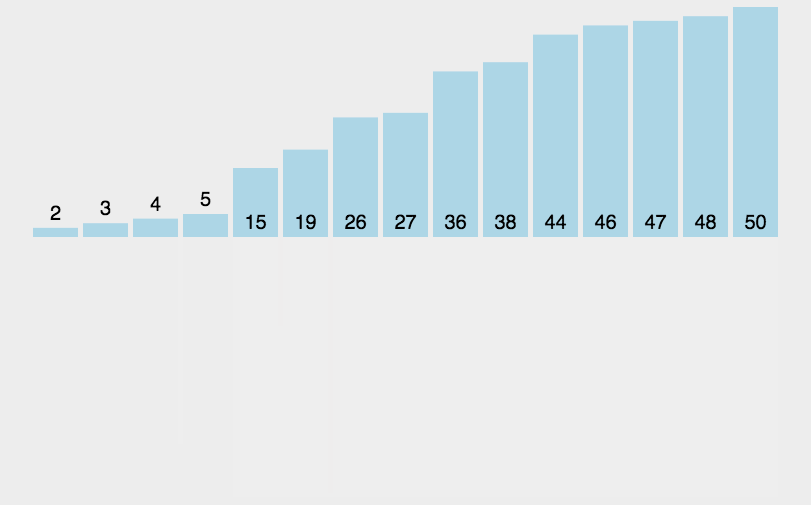
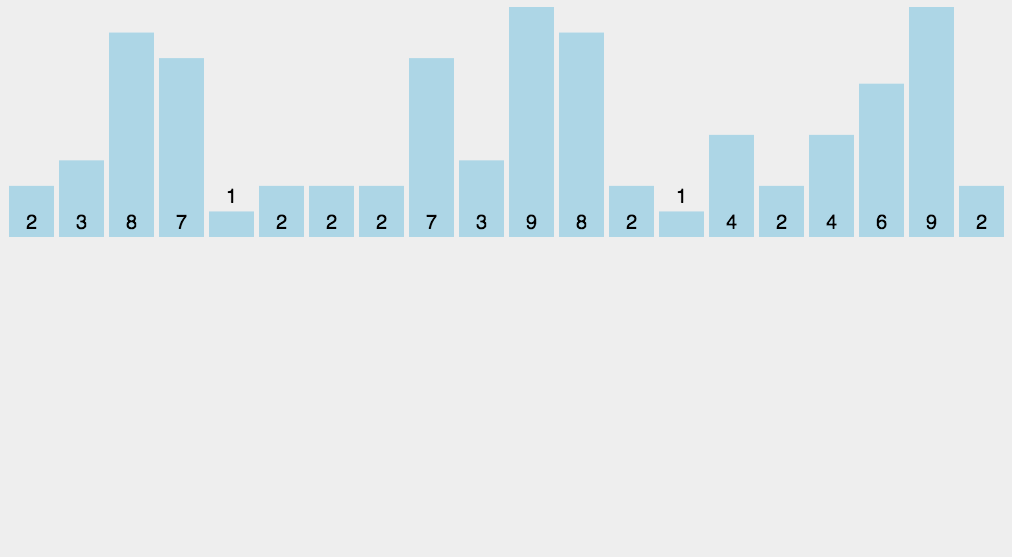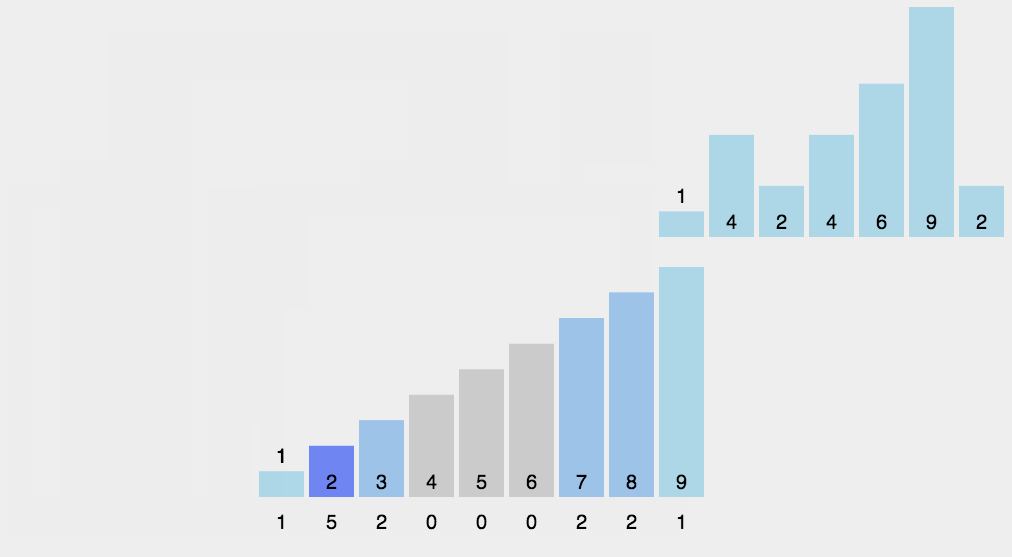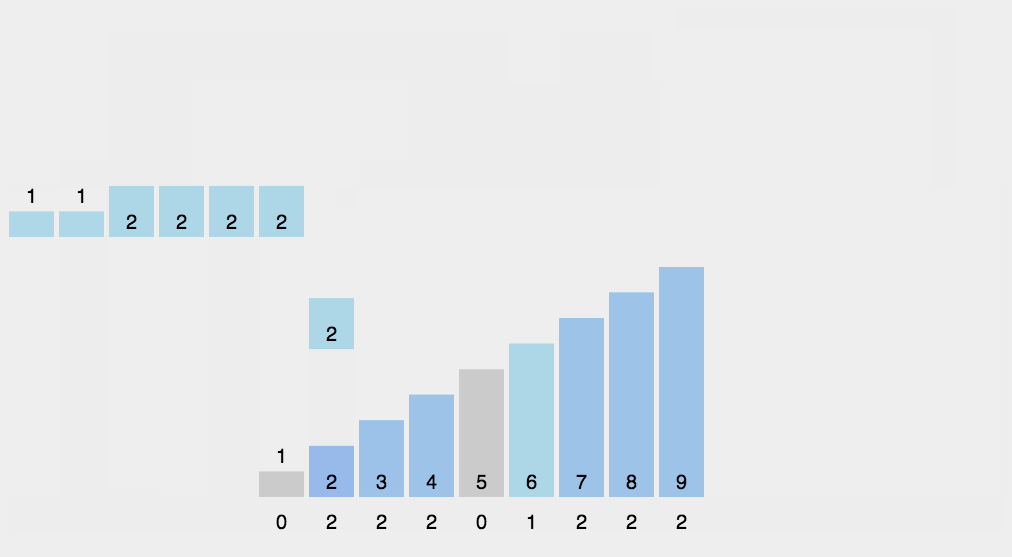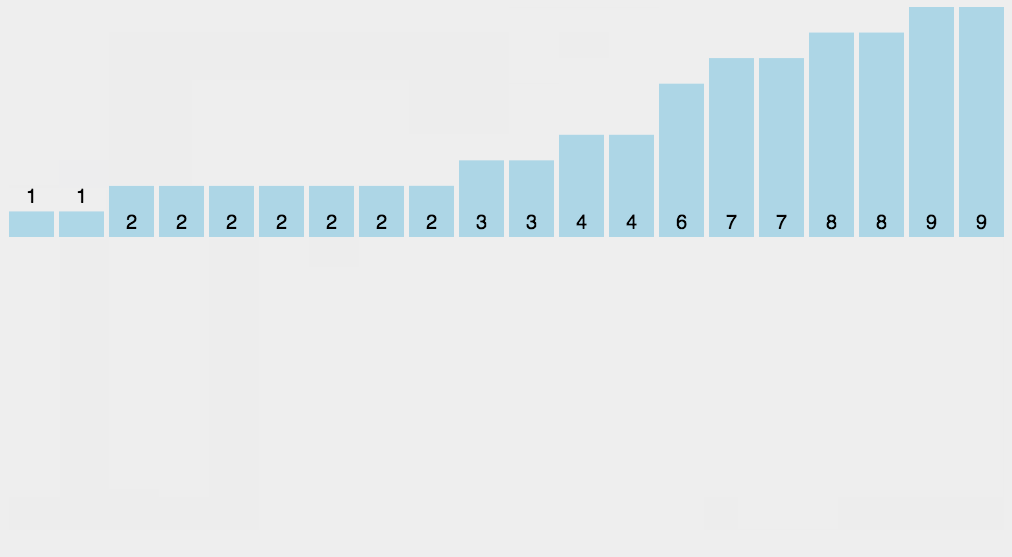玩转十大经典排序算法（动图+Java代码）

排序算法是最基础的算法知识，也是面试笔试中必考的问题！！！！

• 笔试题中主要是各个算法的复杂度，稳定性，所属类型和模拟几次实现结果之类的问题
  通过本文的两张总结图和10张算法动态图基本都可以迎刃而解

• 面试题中当然就是手撕代码了，自己实现一个排序方法，如果没有较好的准备，很容易就蒙圈。虽然大家在数据结构课程都学过大部分的排序算法了，但是知道原理和手写出来还是有很大区别的。

现在我就将这十种排序算法的Java代码实现也记录在这里，方便自己复习，也方便同样在准备找工作的同学

本文图片大多数都转自这里，感谢这个大佬的图，牛批！！ 如果觉得我的总结的不是很清楚可以去看看大佬的思路

下面所有的代码我都经过100000次随机数据的测试了，如果有问题请私聊我及时更正。

各类排序算法的对比与分类

分类记忆

一般手撕代码都会是O(N*logN)的算法,所以一定要能熟练的手写快速排序，归并排序和堆排序

• 初级排序（O(N*2）
  • 选择排序：每次找到最小值，然后放到待排序数组的起始位置
  • 插入排序：从前到后逐步建立有序序列，对于未排序数据，在已排序序列中从后往前扫描，找到对应位置并插入
  • 冒泡排序：嵌套循环，每次查看相邻的元素，如果逆序，则交换
• 高级排序***（O(N*logN))
  • 快速排序：数组取标杆pivot，将元素小的放在pivot左边，大元素放右边，然后依次对左边和右边的子数组继续快速排序，达到整体有序
  • 归并排序：
    • 把长度为n的输入序列分为两个长度为n/2的子序列
    • 对两个子序列分别采用归并排序
    • 将两个排序好的子序列合并成为一个最终序列
  • 堆排序：
    • 数组元素一次建立小顶堆
    • 一次取堆顶元素，并删除
• 特殊排序（O(N)) 针对整数
  • 计数排序（数的范围有限）
    • 统计每个数出现的次数
    • 顺序存入数组
  • 桶排序
    • 每一段数据是一个桶，桶内加入时进行排序
    • 把所有的桶有序拼接，达到整体有序
  • 基数排序
    • 从最低位开始排序
    • 排序好之后再递归调用上一位进行排序
    • 最高位有序后达到最终有序

选择排序

单向选择

i 记录当前有序位
j 记录遍历数组指针
minIndex 记录每次遍历的最小数的下标
每次遍历结束交换 下标为i 和下标为 minIndex 的值

/**
     * 选择排序1
     * 每次遍历查找剩余元素的最小值然后放到对应的位置
     *
     * @param arr
     */
    public static void SelectionSort1(int[] arr) {

        int n = arr.length;
        for (int i = 0; i < n; i++) {
            int minIndex = i;
            for (int j = i; j < n; j++) {
                if (arr[j] < arr[minIndex])
                    minIndex = j;
            }
            swap(arr, i, minIndex);
        }
    }

双向选择

left 记录左侧有序位（从小到大）
right 记录右侧有序位 （从大到小）
类似于单向选择从大到小的排序，双向选择是同时进行从小到大和从大到小的排序
每次遍历获取最大值和最小值并调整到正确位置

	/**
     * 选择排序2
     * 每次遍历查找剩余元素的最小值和最大值然后放到对应的位置
     *
     * @param arr
     */
    public static void SelectionSort2(int[] arr) {

        int left = 0;
        int right = arr.length - 1;

        while (left < right) {
            int minIndex = left;
            int maxIndex = right;


            //每次查找，保证arr[minIndex] <= arr[maxIndex]
            if (arr[minIndex] > arr[maxIndex]) {
                swap(arr, minIndex, maxIndex);
            }
            //从left+1到right-1遍历，找出最大最小
            for (int i = left + 1; i < right; i++) {
                if (arr[i] < arr[minIndex])
                    minIndex = i;
                else if (arr[i] > arr[maxIndex])
                    maxIndex = i;
            }

            swap(arr, left, minIndex);
            swap(arr, right, maxIndex);

            left++;
            right--;
        }

    }

插入排序

依次交换

从i位置向前依次进行比较，如果比本身大，就交换一下，直到正确位置

     /**
     * 插入排序1
     * 和前一个一次交换，直到正确位置
     *
     * @param arr
     */
    public static void InsertionSort1(int[] arr) {

        int n = arr.length;
        for (int i = 0; i < n; i++) {
            //寻找arr[i]适合的地方插入
            for (int j = i; j > 0 && arr[j] < arr[j - 1]; j--) {
                swap(arr, j, j - 1);
            }
        }
    }

依次覆盖

先暂存本身的值
从 i 位置开始向前遍历，如果arr[j-1[>arr[j] 就让arr[j-1[覆盖arr[j[的值，直到找到正确位置，将本身的值填进去

	/**
     * 插入排序2
     * 暂存插入的数据
     * 将前一个元素循环赋值给后一个元素，当发现正确位置后，将暂存数据放到对应位置
     *
     * @param arr
     */
    public static void InsertionSort2(int[] arr) {

        int n = arr.length;
        for (int i = 0; i < n; i++) {
            int e = arr[i];
            int j = i;
            for (; j > 0 && e < arr[j - 1]; j--) {
                arr[j] = arr[j - 1];
            }
            arr[j] = e;
        }
    }

冒泡排序

常规冒泡

从第一个数开始遍历，发现大于后面的数就交换，交换之后继续比较，直到有序

	/**
     * 冒泡排序1
     * 从头到尾全部遍历了
     *
     * @param arr
     */
    public static void BubbleSort1(int[] arr) {

        int n = arr.length;
        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < n - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    swap(arr, j, j + 1);
                }
            }
        }
    }

优化冒泡

从第一个数开始遍历，发现大于后面的数就交换，交换之后继续比较
每次交换都记录下标记位，最后一次更新的标记位后都是有序的了，外层遍历到标记位就退出，减少了遍历次数，如果是基本有序的，最好情况可升级至O(N)

	 /**
     * 冒泡排序2
     * 如果后面m个有序，记录位置，每次遍历到有序位就跳出来
     *
     * @param arr
     */
   public static void BubbleSort2(int[] arr) {

        int n = arr.length;
        int new_n;
        while (n > 0) {
            new_n = 0;
            for (int i = 1; i < n; i++) {
                if (arr[i - 1] > arr[i]) {
                    swap(arr, i, i - 1);
                    new_n = i;//每次交换记录交换位置，最后一次交换位置之后都是有序的了
                }
            }
            n = new_n;
        }
    }

希尔排序

	/**
     * 希尔排序
     * @param arr
     */
    public static void ShellSort(int[] arr) {

        int n = arr.length;
        //增量
        int gap = 1;
        while (gap < n / 3) {
            gap = gap * 3 + 1;
        }
        while (gap >= 1) {
            for (int i = gap; i < n; i++) {
                //使用插入排序
                int e = arr[i];
                int j = i;
                for (; j >= gap && e < arr[j - gap]; j -= gap) {
                    arr[j] = arr[j - 1];
                }
                arr[j] = e;
            }
            gap /= 3;
        }
    }

归并排序

 /**
     * 归并排序递归方法体
     *
     * @param arr
     * @param l
     * @param mid
     * @param r   将arr[l...mid]和arr[mid+1...r]两部分进行归并
     */
    private static void merge(int[] arr, int l, int mid, int r) {
        int[] tmp = new int[r - l + 1];//中间数组
        int i = l;//前半段下标
        int j = mid + 1;//后半段下标
        int k = 0;//新数组下标
        while (i <= mid && j <= r) {
            tmp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
        }
        while (i <= mid) tmp[k++] = arr[i++];
        while (j <= r) tmp[k++] = arr[j++];

        //复制到原数组去
        for (int m = 0; m < tmp.length; m++) {
            arr[l + m] = tmp[m];
        }
    }

    //递归调用归并排序，对arr[l...r]的范围进行排序
    private static void MergeSorts(int[] arr, int l, int r) {

        if (l >= r) {
            return;
        }

        int mid = (l + r) >> 1;

        //下探到下一层进行归并
        MergeSorts(arr, l, mid);
        MergeSorts(arr, mid + 1, r);

        //本层操作，进行归并排序
        merge(arr, l, mid, r);

    }

    /**
     * 归并排序
     *
     * @param arr
     */
    public static void MergeSort(int[] arr) {
        MergeSorts(arr, 0, arr.length - 1);
    }

快速排序

普通快速排序

• 每次选第一个数称为 “基准”（pivot）；
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序

	//对arr[l...r]部分进行partition
    private static int partition(int[] arr, int l, int r) {

        //暂存arr[l]
        int v = arr[l];
        //j为分割位
        int j = l;
        for (int i = l + 1; i <= r; i++) {
            if (arr[i] < v) {
                j++;
                //将小于v的这个数和第一个大于v的数交换
                swap(arr, j, i);
            }
        }
        //将v交换到分割位
        swap(arr, l, j);

        return j;
    }


    //递归使用快速排序
    private static void quickSort1(int[] arr, int l, int r) {

        if (l >= r) {
            return;
        }


        //获取l位置这个数的正确位置
        int p = partition(arr, l, r);

        //小于v的部分递归
        quickSort1(arr, l, p - 1);
        //大于v的部分递归
        quickSort1(arr, p + 1, r);

    }
	//主调用
    static void quickSort1(int[] arr) {
        quickSort1(arr, 0, arr.length - 1);
    }


    private static void swap(int[] arr, int i, int j) {
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

随机化快速排序

每次都从第一个数作为基准，最坏情况下会退化成n^2

改进：将基准的获取随机化，期望变为nlogn

swap( arr, l , (int)(Math.random()*(r-l+1))+l );

修改partition，添加上随机化代码

	//对arr[l...r]部分进行partition
    private static int partition(int[] arr, int l, int r) {

        // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
        swap( arr, l , (int)(Math.random()*(r-l+1))+l );


        //暂存arr[l]
        int v = arr[l];
        //j为分割位
        int j = l;
        for (int i = l + 1; i <= r; i++) {
            if (arr[i] < v) {
                j++;
                //将小于v的这个数和第一个大于v的数交换
                swap(arr, j, i);
            }
        }
        //将v交换到分割位
        swap(arr, l, j);

        return j;
    }

双路快速排序

图自慕课网bobo老师的算法与数据结构课程！

i索引不断向后扫描，当i的元素小于v的时候继续向后扫描，直到碰到了某个元素大于等于v。j同理，直到碰到某个元素小于等于v。

然后绿色的部分便归并到了一起，而此时只要交换i和j的位置就可以了，然后i++，j–就行了。

代码仅需要修改partition

 // 双路快速排序的partition
    // 返回p, 使得arr[l...p-1] <= arr[p] ; arr[p+1...r] >= arr[p]
    //对arr[l...r]部分进行partition
    private static int partition(int[] arr, int l, int r) {

        // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
        swap(arr, l, (int) (Math.random() * (r - l + 1)) + l);


        //暂存arr[l]
        int v = arr[l];

        //j为分割位
        int i = l + 1, j = r;
        while (true) {

            //从前面开始。小于v的不变
            while (i <= r && arr[i] < v) {
                i++;
            }
            //从后面开始。大于v不变
            while (j >= l + 1 && arr[j] > v) {
                j--;
            }

            if (i > j) {
                break;
            }

            //到这里了: arr[i]>=v arr[j]<=v
            //如果等于v也要换，保证了两边相等的数目平衡

            swap(arr, i, j);
            i++;
            j--;
        }
        swap(arr, l, j);
        return j;
    }

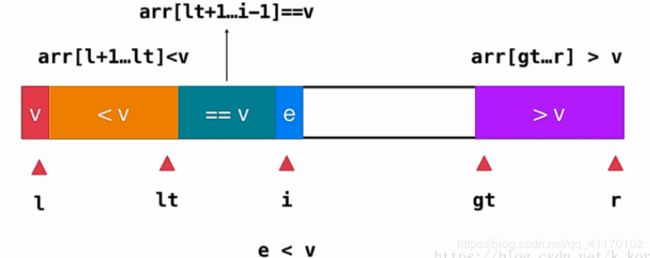
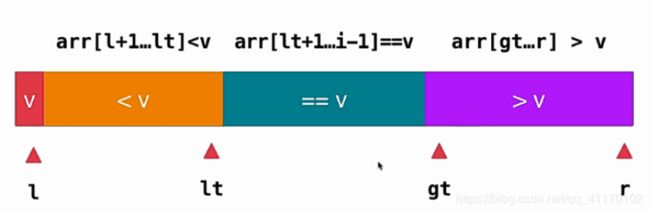
三路快速排序

当重复数字较多时，以上三种快速排序效率都很低，所以需要将==v单独进行处理，具体如图和代码，感觉看代码比说更清楚

 	// 三路快速排序的partition
    //对arr[l...r]部分进行partition
    private static void quickSort3(int[] arr, int l, int r) {

        if (l > r) {
            return;
        }

        // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
        swap(arr, l, (int) (Math.random() * (r - l + 1)) + l);


        //暂存arr[l]
        int v = arr[l];

        //j为分割位
        int lt = l;
        int gt = r + 1;
        int i = l + 1;
        while (i < gt) {

            if (arr[i] < v) {
                swap(arr, i, lt + 1);
                i++;
                lt++;
            } else if (arr[i] > v) {
                swap(arr, i, gt - 1);
                gt--;
            } else {
                i++;
            }
        }
        swap(arr, l, lt);

        //小于v的部分递归
        quickSort3(arr, l, lt - 1);
        //大于v的部分递归
        quickSort3(arr, gt, r);

    }


    static void quickSort3(int[] arr) {
        quickSort3(arr, 0, arr.length - 1);
    }


    private static void swap(int[] arr, int i, int j) {
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

堆排序

优先队列

个人觉得这个很丑，面试要被怼，不过也算是一种方法嘛，利用了Java的优先队列底层是小顶堆的特性，只要存入优先队列再取出来就是按堆排序实现了

	static void heapSort(int[] arr) {

        PriorityQueue<Integer> pq = new PriorityQueue<>();

        for (int i = 0; i < arr.length; i++) {
            pq.add(arr[i]);
        }
        for (int i = 0; i < arr.length; i++) {
            arr[i] = pq.remove();
        }

    }

原地堆

上面的图就是原地堆的，看不懂我写的就看图吧！！！

首先直接把传入的数组就当做无序的完全二叉树

先判断最后一个非叶子节点的位置，从它开始向前进行siftDown操作

这样，我们就构建成了一个大顶堆，堆顶就是最大值啦

然后把最大值放到倒数对应的位置去，后面的数就有序了

后面的数移到堆顶打破了堆的结构，再次进行siftDown操作，这时候就要限制siftDown操作的堆的范围了，只在无序的部分进行siftDown操作

最终所有值都放到对应的位置

	static void heapSort2(int[] arr) {

        int n = arr.length;

        // 注意，此时我们的堆是从0开始索引的
        // 从(最后一个元素的索引-1)/2开始(最后一个叶子节点父节点)
        // 最后一个元素的索引 = n-1
        for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
            siftDown(arr, n, i);
        }

        for (int i = n - 1; i > 0; i--) {
            swap(arr, 0, i);
            siftDown(arr, i, 0);
        }

    }

    /**
     *
     * @param arr 堆数组
     * @param n 有序的位置
     * @param k 当前位置
     */
    private static void siftDown(int[] arr, int n, int k) {
        while (2 * k + 1 < n) {
            //默认左孩子
            int j = 2 * k + 1;
            //看下有没有右孩子并且比左孩子大，如果有，就让它浮上去
            if (j + 1 < n && arr[j + 1] > arr[j])
                j += 1;

            if (arr[k] >= arr[j]) break;
            //孩子比父节点大，浮上去
            swap(arr, k, j);
            k = j;
        }
    }

    private static void swap(int[] arr, int i, int j) {
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

计数排序

• 找出待排序的数组中最大和最小的元素；
• 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
• 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
• 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

	/**
     * 计数排序
     *
     * @param arr
     */
    static void countSort(int[] arr) {

        //获取数列的最大值和最小值，并求出差值
        int max = arr[0];
        int min = arr[0];
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] > max)
                max = arr[i];
            if (arr[i] < min)
                min = arr[i];
        }
        int d = max - min;

        //常见统计数组并统计对饮元素的个数
        int[] countArr = new int[d + 1];
        for (int i = 0; i < arr.length; i++) {
            countArr[arr[i] - min]++;
        }

        //统计数组做变形，后面额元素等于前面的元素之和

        int sum = 0;
        for (int i = 0; i < countArr.length; i++) {
            sum += countArr[i];
            countArr[i] = sum;
        }

        //倒序遍历原始数列，从统计数字找出正确位置
        int[] res = new int[arr.length];
        for (int i = arr.length - 1; i >= 0; i--) {
            res[countArr[arr[i] - min] - 1] = arr[i];
            countArr[arr[i] - min]--;
        }


        //复制数据到原数组
        System.arraycopy(res,0,arr,0,res.length);
        
    }

桶排序

• 设置一个定量的数组当作空桶，代码是假定传入为[0，10）之间的浮点数，以[0,9]的整数为桶
• 遍历输入数据，并且把数据一个一个放到对应的桶里去；
• 对每个不是空的桶进行排序；
• 从不是空的桶里把排好序的数据拼接起来

 	 /**
     * 桶排序
     * 假定传入为[0，10）之间的浮点数，以[0,9]的整数为桶
     *
     * @param arr
     */
    private static void bucketSort(double[] arr) {
        //创建桶的集合
        ArrayList<LinkedList<Double>> buckets = new ArrayList<>();
        for (int i = 0; i < 10; i++) {
            buckets.add(new LinkedList<Double>());
        }

        //将数据放入桶并排序
        for (double data : arr) {
            //获取数据对应的桶序号
            int index = getIndex(data);
            //将数据放入桶并在桶内排序
            insertAndSort(buckets.get(index), data);
        }

        //将数据取出来
        int index = 0;
        for (LinkedList<Double> bucket : buckets) {
            for (double data : bucket) {
                arr[index++] = data;
            }
        }


    }

    //放入桶并排序
    private static void insertAndSort(LinkedList<Double> buckets, double data) {
        buckets.add(data);
        //排序，double比较需要重写一下比较规则
        buckets.sort(new Comparator<Double>() {
            @Override
            public int compare(Double o1, Double o2) {
                return o1.compareTo(o2);
            }
        });


    }

    //自定义规则的桶划分
    private static int getIndex(double data) {
        return (int) data;
    }

基数排序

• 取得数组中的最大数，并取得位数；
• arr为原始数组，从最低位开始取每个位组成radix数组；
• 对radix进行计数排序（利用计数排序适用于小范围数的特点）

	/**
     * 基数排序
     *
     * @param arr
     */
    private static void radixSort(int[] arr) {

        int n = arr.length;

        //find max
        int max = arr[0];
        for (int i = 1; i < n; i++) {
            if (arr[i] > max)
                max = arr[i];
        }
        //求最大值的位数
        int keyNum = 0;
        while (max > 0) {
            max /= 10;
            keyNum++;
        }

        //构建并初始化桶集合
        ArrayList<LinkedList<Integer>> buckets = new ArrayList<>();
        for (int i = 0; i < 10; i++) {
            buckets.add(new LinkedList<>());
        }

        for (int i = 0; i < keyNum; i++) {
            radixSort(arr, buckets, i);
        }


    }

    /**
     * 装入bucket后再写入arr
     * @param arr
     * @param buckets
     * @param num
     */
    private static void radixSort(int[] arr, ArrayList<LinkedList<Integer>> buckets, int num) {

        //将数据存入bucket
        for (int i = 0; i < arr.length; i++) {
            //获取key
            int key = (int) (arr[i] % Math.pow(10, num + 1) / Math.pow(10, num));
            
            buckets.get(key).add(arr[i]);
        }

        //读取数据到arr
        int count = 0;
        for (int i = 0; i < 10; i++) {
            LinkedList<Integer> bucket = buckets.get(i);
            while (!bucket.isEmpty()){
                arr[count++] = bucket.remove();
            }

        }


    }

排序的应用题

在熟悉上述的排序算法之后，一起尝试做一做下面几个算法题吧

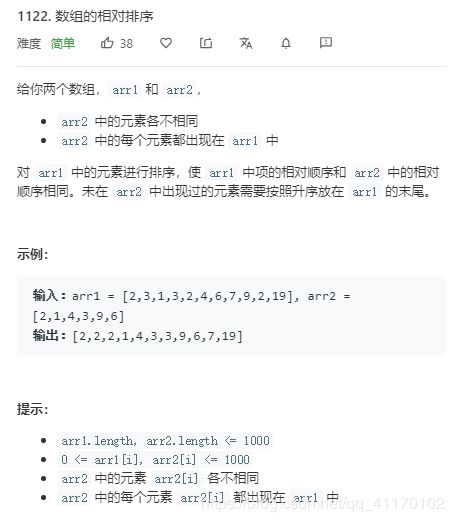
1122.数组的相对排序

计数排序：

public class Solution {

    public int[] relativeSortArray(int[] arr1, int[] arr2) {
        //计数容器
        int[] arr = new int[1001];
        
        //arr1加入计数容器后就没用了，所以不开辟额外内存空间记录结果，直接用arr1

        int index = 0;//索引下标
        //将arr1存入计数容器
        for (int num : arr1) {
            arr[num]++;
        }
        //查找arr2有的数按计数顺序加入arr1
        for (int num : arr2) {
            while (arr[num]-- > 0) {
                arr1[index] = num;
                index++;
            }
        }
        //arr2没有的数顺序加入结尾
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] != 0) {
                while (arr[i]-- > 0) {
                    arr1[index] = i;
                    index++;
                }
            }
        }
        return arr1;
    }
}

56.合并区间

排序思想的运用+贪心

class Solution {
    public int[][] merge(int[][] intervals) {
        List<int[]> res = new ArrayList<>();//区间记录集合
        //以区间头排序
        Arrays.sort(intervals, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[0] - o2[0];
            }
        });
        int start = 0;//区间起始位置
        int end = 0;//区间结束位置
        int index = 0;//区间下标

        while (index < intervals.length) {
            //初始化区间的首尾
            start = intervals[index][0];
            end = intervals[index][1];
            index++;
            //如果区间的首部小于上一个的尾部，说明有重复
            while (index < intervals.length && end >= intervals[index][0]) {
                //如果区间的尾部小于等于上一个的尾部，说明整个区间被包含，不需要变动
                if (end >= intervals[index][1]) {
                    index++;
                } else {//如果区间的尾部大于上一个的尾部，说明需要更新end
                    end = intervals[index][1];
                    index++;
                }
            }
            res.add(new int[]{start, end});
        }

        int[][] ret = res.toArray(new int[res.size()][]);
        return ret;
    }
}

面试题51.数组中的逆序对

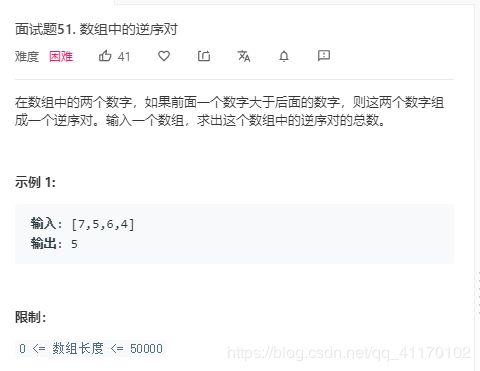
归并排序
标准的归并排序模板，每次比较时，如果右边的小于左边的，那么右边那个数小于左边的数及其后面的所有数
归并是每两个数只比较一次的，所以不会存在重复

public class Solution {
    public int reversePairs(int[] nums) {
        return mergeSort(nums, 0, nums.length - 1);
    }

    private int mergeSort(int[] nums, int left, int right) {
        if (left >= right) return 0;
        int mid = (left + right) >> 1;
        //将归并的所有结果汇总返回
        return mergeSort(nums, left, mid) + mergeSort(nums, mid + 1, right) + merge(nums, left, mid, right);
    }

    private int merge(int[] nums, int left, int mid, int right) {
        int i = left;
        int j = mid + 1;
        int k = 0;
        int count = 0;
        int res[] = new int[right - left + 1];
        while (i <= mid && j <= right) {
            if (nums[i] > nums[j]) count += mid - i + 1;//如果j位置小于i位置，那么j位置小于i位置后所有的左半边的数
            res[k++] = nums[i] <= nums[j] ? nums[i++] : nums[j++];
        }
        while (i <= mid) res[k++] = nums[i++];
        while (j <= right) res[k++] = nums[j++];
        for (int m = 0; m < res.length; m++) {
            nums[left + m] = res[m];
        }
        return count;
    }
}

493.翻转对

归并排序

和逆序对非常相似，看似只差一个*2，其实里面有坑！
逆序对中：归并时如果num[i]>nums[j]是一定能找到的，如果没有就是真的没有。如{1,2,3,4}，没有就是真的没有
翻转对中： nums[i]>2*nums[j]就不一定在归并过程中能找到了。如{3,4,8,9,1.2,3,3}，左边最多只能移动到4，不满足，就不能获得值了

所以，不能把统计放在归并过程中，需要单独提出来统计

		//因为是2倍的比较，所以在归并中不一定会出现nums[i]>2*nums[j]
        //所以不能放入归并流程中进行查找，单独拿出来遍历获取
        int tmpi = left;//临时计算使用i
        int tmpj = mid + 1;//临时计算使用j
        while (tmpj <= right) {
            //如果不满足条件，向后移动i
            while (tmpi <= mid && nums[tmpi] <= 2 *(long) nums[tmpj]) tmpi++;
            //满足条件了，正常计数
            count += mid - tmpi + 1;//如果j位置小于i位置，那么j位置小于i位置后所有的左半边的数
            tmpj++;
        }

维护一个j指针，然后j指针依次顺移，如果有i指针满足，则i及i后面的值都可以和j组成一个逆序对

整体代码：

public class Solution {
    public int reversePairs(int[] nums) {
        return mergeSort(nums, 0, nums.length - 1);
    }

    private int mergeSort(int[] nums, int left, int right) {
        if (left >= right) return 0;
        int mid = (left + right) >> 1;
        //将归并的所有结果汇总返回
        return mergeSort(nums, left, mid) + mergeSort(nums, mid + 1, right) + merge(nums, left, mid, right);
    }

    private int merge(int[] nums, int left, int mid, int right) {

        int i = left;
        int j = mid + 1;
        int k = 0;
        int count = 0;
        int res[] = new int[right - left + 1];

        //因为是2倍的比较，所以在归并中不一定会出现nums[i]>2*nums[j]
        //所以不能放入归并流程中进行查找，单独拿出来遍历获取
        int tmpi = left;//临时计算使用i
        int tmpj = mid + 1;//临时计算使用j
        while (tmpj <= right) {
            //如果不满足条件，向后移动i
            while (tmpi <= mid && nums[tmpi] <= 2 *(long) nums[tmpj]) tmpi++;
            //满足条件了，正常计数
            count += mid - tmpi + 1;//如果j位置小于i位置，那么j位置小于i位置后所有的左半边的数
            tmpj++;
        }


        while (i <= mid && j <= right) {
            res[k++] = nums[i] <= nums[j] ? nums[i++] : nums[j++];
        }
        while (i <= mid) res[k++] = nums[i++];
        while (j <= right) res[k++] = nums[j++];
        for (int m = 0; m < res.length; m++) {
            nums[left + m] = res[m];
        }

        return count;
    }

    public static void main(String[] args) {
        int i = new Solution().reversePairs(new int[]{1, 3, 2, 3, 1});
        System.out.println(i);
    }
}

---

更多Java面试复习笔记和总结可访问我的面试复习专栏《Java面试复习笔记》，或者访问我另一篇博客《Java面试核心知识点汇总》查看目录和直达链接