ML与math：机器学习与高等数学基础概念、代码实现、案例应用之详细攻略——基础篇

ML与math：机器学习与高等数学基础概念、代码实现、案例应用之详细攻略——基础篇

 

 

目录

一、ML与高等数学

0、基础数学

1、导数、方向导数、梯度

1.1、概念简介

1.2、代码实现

2、Taylor展开

3、凸函数

二、ML与概率统计

1、古典概率

2、贝叶斯公式

3、常见概率分布

4、重要统计量(基于全局的而不是样本)

5、不等式系列

6、样本估计参数

7、先验概率、后验概率

三、ML与线性代数

---

 

 

 

 

 

 

相关文章
DL之simpleNet：利用自定义的simpleNet(设好权重)对新样本进行预测、评估、输出梯度值

 

一、ML与高等数学

0、基础数学

(1)、平方根：一般若干次(5、6次)迭代即可获得比较好的近似值。

(2)、拉格朗日函数解决带约束的优化问题

 

 

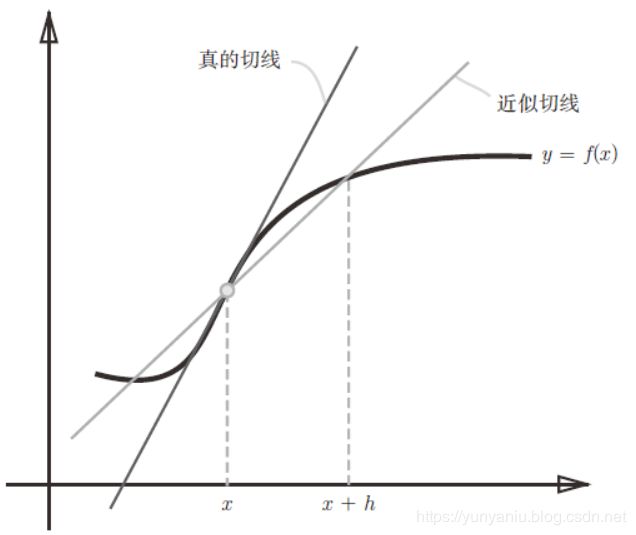
1、导数、方向导数、梯度

1.1、概念简介

(1)、已知函数f(x)=x^x，x>0，求f(x)的最小值：在信息熵中会遇到

(2)、方向导数、梯度

 

1.2、代码实现

(1)、求导：利用微小的差分求导数的过程称为数值微分(numerical differentiation)

#利用微小的差分求导数的过程称为数值微分(numerical differentiation)
def numerical_diff(f, x):
    h = 1e-4 # 0.0001
    return (f(x+h) - f(x-h)) / (2*h)

(2)、实现简单的函数求导

import numpy as np
import matplotlib.pylab as plt


def numerical_diff(f, x):
    h = 1e-4 # 0.0001
    return (f(x+h) - f(x-h)) / (2*h)

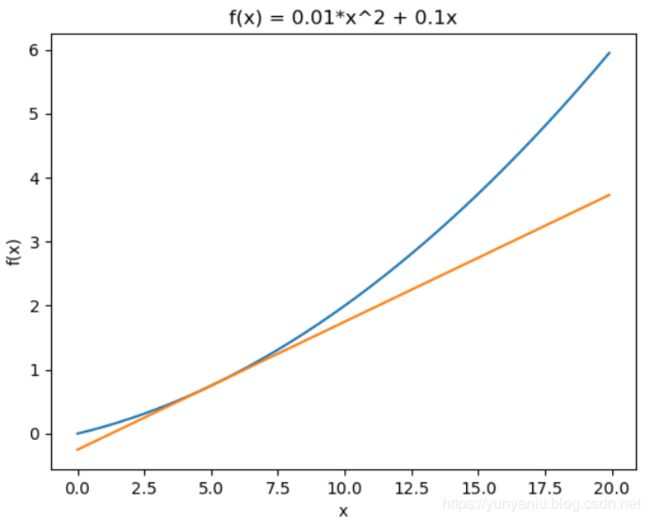
def function_1(x):
    return 0.01*x**2 + 0.1*x

def tangent_line(f, x):
    d = numerical_diff(f, x)
    print(d)
    y = f(x) - d*x
    return lambda t: d*t + y

x = np.arange(0.0, 20.0, 0.1) # 以0.1为单位，从0到20的数组x
y = function_1(x)

tf = tangent_line(function_1, 5)
y2 = tf(x)

plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x, y)
plt.plot(x, y2)
plt.title('f(x) = 0.01*x^2 + 0.1x')
plt.show()


#对函数求导：在x=5 和x=10 处的导数
#利用微小的差分求导数的过程称为数值微分(numerical differentiation)


print('x=5 处求导：',numerical_diff(function_1, 5))
print('x=10 处求导：',numerical_diff(function_1, 10))
#和真实结果对比，发现虽然严格意义上并不一致，但误差非常小。实际上，误差小到基本上可以认为它们是相等的。


0.1999999999990898
x=5 处求导： 0.1999999999990898
x=10 处求导： 0.2999999999986347

(3)、求偏导数

    

(4)、梯度法求的最小值

(5)、综合案例

输出结果

求x0=3, x1=4时，关于x0的偏导数： 6.00000000000378
求x0=3, x1=4时，关于x1的偏导数： 7.999999999999119

求点(3, 4)、(0, 2)、(3, 0) 处的梯度
[6. 8.]
[0. 4.]
[6. 0.]

求函数最小值： [-6.11110793e-10  8.14814391e-10]
学习率过大的例子：lr=10.0： [-2.58983747e+13 -1.29524862e+12]
学习率过小的例子：lr=1e-10： [-2.99999994  3.99999992]

输出权重参数：
[[-1.20419093  2.09426703  1.46228252]
 [ 1.74419802  0.55102885  1.2495018 ]]

输出预测： [0.84726366 1.75248618 2.00192113]
最大值的索引： 2
loss： 0.7392699844784301

求出梯度值： 
 [[ 0.09028775  0.22323484 -0.31352259]
 [ 0.13543162  0.33485226 -0.47028388]]

实现代码
ML之Math：理解机器学习的数学基础之求导、求偏导、求梯度、定义梯度下降算法(并尝试调参lr)

 

 

2、Taylor展开

(1)、Taylor公式的应用：求e^x

(2)、Taylor公式的应用：

 

3、凸函数

   

(1)、凸函数的判定：
定理：f(x)在区间[a,b]上连续，在(a,b)内二阶可导，那么：
  若f’’(x)>0，则f(x)是凸的；
  若f’’(x)<0，则f(x)是凹的
即：一元二阶可微的函数在区间上是凸的，当且仅当它的二阶导数是非负的
(2)、凸函数性质的应用：下边的式子在最大熵模型内容

 

 

 

二、ML与概率统计

概率与统计，其实关注的是两个不同类的点，实际上是两个相反的思路。
概率：已知总体，去求具体事件A的概率；
统计：已知某件事B发生，估计产生事件B的总体概率是多少。

(1)、生日悖论

(2)、将12件正品和3件次品随机装在3个箱子中。每箱中恰有1件次品的概率是多少？
解：将15件产品装入3个箱子，每箱装5件，共有15!/(5!5!5!)种装法；
 先把3件次品放入3个箱子，有3!种装法。对于这样的每一种装法，把其余12件产品装入3个箱子，每箱装4件，共有12!/(4!4!4!)种装法；
 P(A)= (3!*12!/(4!4!4!)) / (15!/(5!5!5!)) = 25/91

 

 

1、古典概率

(1)、举例：将n个不同的球放入N(N≥n)个盒子中，假设盒子容量无限，求事件A={每个盒子至多有1个球}的概率。

 

 

2、贝叶斯公式

 

3、常见概率分布

(0)、统计参数总结：

均值	期望，一阶
方差	标准差，二阶  1)、变异系数Coefficient of Variation：标准差与平均数的比值称为变异系数，记为C·V
偏度	Skew三阶。 (1)、偏度衡量随机变量概率分布的不对称性，是概率密度曲线相对于平均值不对称程度的度量。 (2)、三阶累积量与二阶累积量的1.5次方的比率。偏度有时用Skew[X]来表示。 (3)、偏度的值可以为正，可以为负或者无定义。 偏度为负(负偏态)意味着在概率密度函数左侧的尾部比右侧的长，绝大多数的值(包括中位数在内)位于平均值的右侧。 偏度为正(正偏态)意味着在概率密度函数右侧的尾部比左侧的长，绝大多数的值(包括中位数在内)位于平均值的左侧。 偏度为零表示数值相对均匀地分布在平均值的两侧，但不一定意味着一定是对称分布。
峰度	Kurtosis四阶   (1)、峰度是概率密度在均值处峰值高低的特征，通常定义四阶中心矩除以方差的平方减3。 (1)、也被称为超值峰度(excess kurtosis)。“减3”是为了让正态分布的峰度为0。 超值峰度为正，称为尖峰态(leptokurtic)；超值峰度为负，称为低峰态(platykurtic)

1)、统计参数应用举例：特异值处理

 

 

 

(1)、两点分布(0-1分布)、二项分布、泊松分布、均匀分布、指数分布(其无记忆性)、正态分布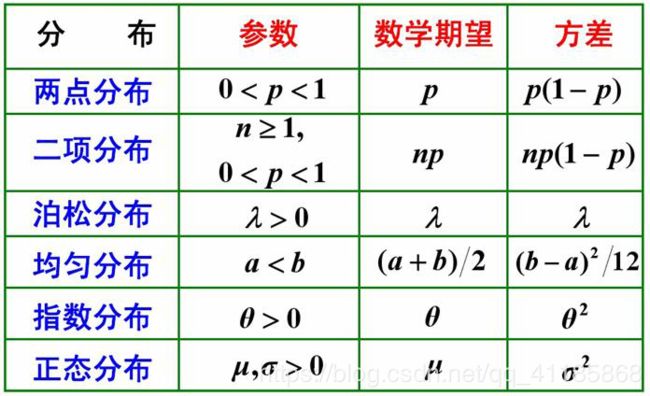

(2)、概率题转为图求解
      A、B两国元首相约在首都机场晚20点至24点交换一份重要文件。如果A国的飞机先到，A会等待1个小时；如果B国的飞机先到了，B会等待2个小时。假设两架飞机在20点至24点降落机场的概率是均匀分布，试计算能够在20点至24点完成交换的概率。注：假设交换文件本身不需要时间。

解：假定A到达的时刻为x，B达到的时刻为y，则完成交接需满足0  同时要求20  由于x，y系数都为1，为作图方便，可以将24

三角形面积9/2、2，矩形面积16，概率19/32

(3)、一定接受率下的采样
已知有个rand7()的函数，返回1到7随机自然数，让利用这个rand7()构造rand10() 随机1~10。
 解：因为rand7仅能返回1~7的数字，少于rand10的数目。因此，多调用一次，从而得到49种组合。超过10的整数倍部分，直接丢弃。

 

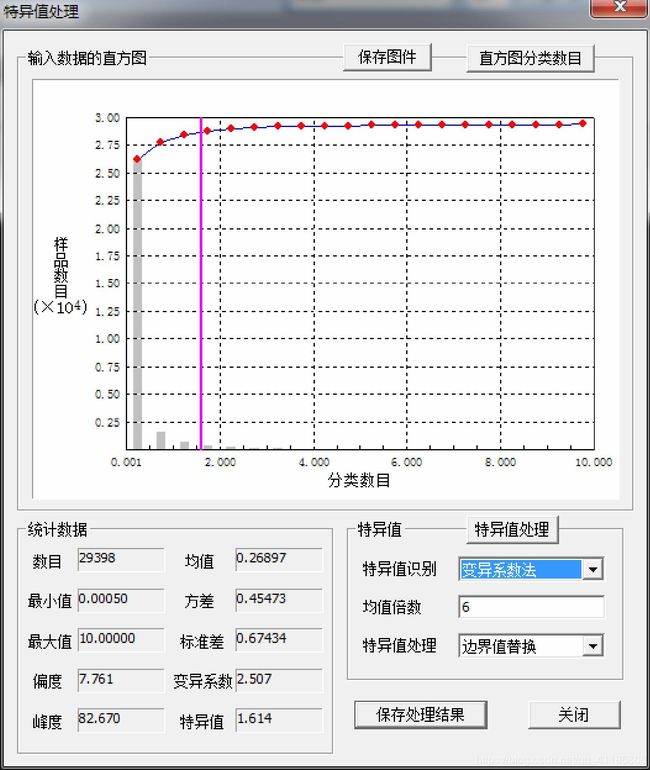
4、重要统计量(基于全局的而不是样本)

(1)、期望与方差
期望：可以理解为这个变量的平均值，是对随机变量本身“客观价值”的一种表现。因为随机无法确定，大家心里需要有个数，这个随机的因素到底围绕的哪条线变化，期望就是那条线。
方差：是另一种特征，他描述的是随机变量的波动性（围绕着期望波动）的大小。方差越大，说明这个事变数越大，容易偏离平均值很远。

(2)、协方差与相关系数
协方差：两个变量在变化过程中是同方向变化？还是反方向变化？同向或反向程度如何？  你变大，同时我也变大，说明两个变量是同向变化的，这时协方差就是正的。  你变大，同时我变小，说明两个变量是反向变化的，这时协方差就是负的。  从数值来看，协方差的数值越大，两个变量同向程度也就越大。反之亦然。
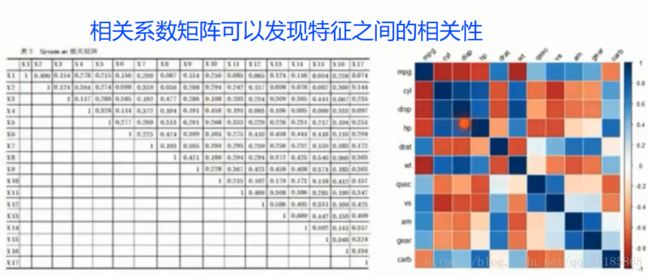
相关系数：是用以反映变量之间相关关系密切程度的统计指标。比如，降维算法就是从10万变量中，挑选相关系数Top1000。

• 相关系数是指利用ML提取的10万个特征向量，分别与标签向量之间得到，从而挑选相关系数。

• 相关系数矩阵可以发现特征之间的相关性，越蓝越靠近1越正相关。

(3)、独立和不相关

 

5、不等式系列

Jensen不等式：

切比雪夫不等式：

大数定律：

中心极限定理：
1、标准的中心极限定理的问题及应用
(1)、有一批样本(字符串)，其中a-z开头的比例是固定的，但是量很大，需要从中随机抽样。样本量n，总体中a开头的字符串占比1%，需要每次抽到的a开头的字符串占比(0.99%,+1.01%)，样本量n至少是多少？
问题重述：大量存在的两点分布Bi(1,p)，其中，Bi发生的概率为0.01，即p=0.01。取其中的n个，使得发生的个数除以总数的比例落在区间(0.0099,0.0101)，则n至少是多少？

2、中心极限定理的意义
 

 

6、样本估计参数

矩估计

极大似然估计

 

7、先验概率、后验概率

(1)、

 

 

三、ML与线性代数

1、矩阵连乘问题从算法到实现
由m[i,j]的递推关系式可以看出，在计算m[i,j]时，需要用到m[i+1,j]，m[i+2,j]…m[j-1,j]；因此，求m[i,j]的前提，不是m[0…i-1;0…j-1] ，而是沿着主对角线开始，依次求取到右上角元素。


(1)、因为m[i,j]一个元素的计算，最多需要遍历n-1次，共O(n2)个元素，故算法的时间复杂度是O(n3)，空间复杂度是O(n2)。