图相关算法之 PageRank 佩奇排序算法详解
- 起源
●网页数量急剧膨胀，用户需要有效搜索出有用的信息
●Google CEO拉里佩奇提出的一种算法，来计算互联网里的网站的重要性，以对搜索进行排名
●PageRank 的计算量很大，因此诞生 了Map-Reduce，分布式计算PageRank
●PageRank 和BigTable (Hbase是Google BigTable 的开源实现)是Google早期的核心
基本思想
●数量假设:在Web图 模型中，如果一个页面节点接收到的其他网页指向的入链数量越多，那么这个页面越重要。
●质量假设:指向页面A的入链质量不同，质量高的页面会通过链接向其他页面传递更多的权重。所以越是质量高(入链数量多)的页面指向页面A，则页面A越重要。即网页质量与数量的加权评判
- PageRank算法计算每一个网页的PageRank值，然后根据这个值
的大小对网页的重要性进行排序。它的思想是随机漫步加网页跳转,即模拟一个悠闲的上
网者,上网者首先随机选择一个网页打开，然后在这个网页上呆了几分钟后，跳转到该网页所指向的链接，这样无所事事、漫无目的地在网页上跳来跳去PageRank就是估计这个悠闲的上网者分布在各个网页上的概率。
算法的数学模型建立:
-
一种结点有两种访问方式:
- 来自其它结点
P R ( u ) = ∑ ν ∈ B u P R ( ν ) L ( ν ) ( 1 ) P R(u)=\sum_{\nu \in B_{u}} \frac{P R(\nu)}{L(\nu)} (1) PR(u)=ν∈Bu∑L(ν)PR(ν)(1) - 被随机访问(浏览器的url输入)
一个节点的影响力 即所有入链集合的页面的加权影响力之和(d为阻尼系数)
P R ( u ) = 1 − d N + d ∑ ν ∈ B u P R ( v ) L ( v ) ( 2 ) P R(u)=\frac{1-d}{N}+d \sum_{\nu \in \mathcal{B}_{u}} \frac{P R(v)}{L(v)}(2) PR(u)=N1−d+dν∈Bu∑L(v)PR(v)(2)
- 来自其它结点
-
公式解释
- (1)中为什么要除以L(V):
为了公平,出链数代表该节点对其它节点的贡献,由于不同节点出链数不一样,对别点节点的贡献次数不一样,就会造成不公平现象,所以要让一个节点对外部其它节点总的贡献都设为1, - (2)中u 为待评估的页面， ν ∈ B u \nu \in B_{u} ν∈Bu中 B u B_{u} Bu 为页面 u 的入链集合。针对入链集合中的任意页面 v，它能给 u带来的影响力是其自身的影响力 PR(v) 除以 v 页面的出链数量，即页面 v 把影响力 PR(v)平均分配给了它的出链，这样统计所有能给 u 带来链接的页面 v，得到的总和就是网页 u的影响力，即为 PR(u)。所以你能看到，出链会给被链接的页面赋予影响力，当我们统计了一个网页链出去的数量，也就是统计了这个网页的跳转概率。
- (1)中为什么要除以L(V):
-
公式(1)的计算例子:
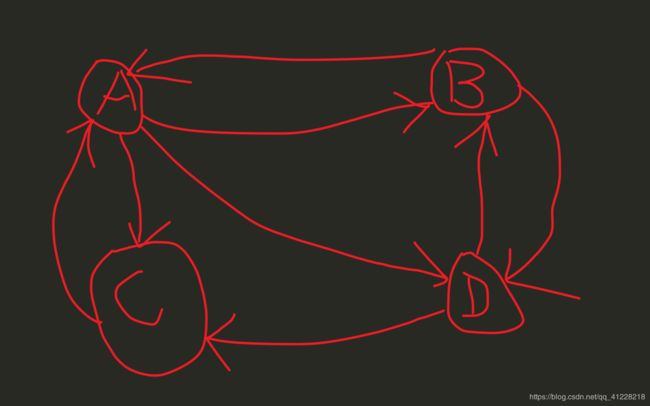
在这个例子中，你能看到 A 有三个出链分别链接到了 B、C、D 上。那么当用户访问 A 的时候，就有跳转到 B、C 或者 D 的可能性，跳转概率均为 1/3。
B 有两个出链，链接到了 A 和 D 上，跳转概率为 1/2。这样，我们可以得到 A、B、C、D 这四个网页的转移矩阵 M：
M = [ 0 1 / 2 1 0 1 / 3 0 0 1 / 2 1 / 3 0 0 1 / 2 1 / 3 1 / 2 0 0 ] \mathrm{M}=\left[\begin{array}{cccc}{0} & {1 / 2} & {1} & {0} \\ {1 / 3} & {0} & {0} & {1 / 2} \\ {1 / 3} & {0} & {0} & {1 / 2} \\ {1 / 3} & {1 / 2} & {0} & {0}\end{array}\right] M=⎣⎢⎢⎡01/31/31/31/2001/2100001/21/20⎦⎥⎥⎤
M = [ A B C D 0 1 2 1 0 1 3 0 0 1 2 1 3 0 0 1 2 1 3 1 2 0 0 ] M=\left[\begin{array}{cccc}{A} & {B} & {C} & {D} \\ {0} & {\frac{1}{2}} & {1} & {0} \\ {\frac{1}{3}} & {0} & {0} & {\frac{1}{2}} \\ {\frac{1}{3}} & {0} & {0} & {\frac{1}{2}} \\ {\frac{1}{3}} & {\frac{1}{2}} & {0} & {0}\end{array}\right] M=⎣⎢⎢⎢⎢⎡A0313131B210021C1000D021210⎦⎥⎥⎥⎥⎤
我们假设 A、B、C、D 四个页面的初始影响力都是相同的，即1/n(n为结点总数)：
w 0 = [ 1 / 4 1 / 4 1 / 4 1 / 4 ] w_{0}=\left[\begin{array}{l}{1 / 4} \\ {1 / 4} \\ {1 / 4} \\ {1 / 4}\end{array}\right] w0=⎣⎢⎢⎡1/41/41/41/4⎦⎥⎥⎤
当进行第一次转移之后，各页面的影响力 变为：
w 1 = M w 0 = [ 0 1 / 2 1 0 1 / 3 0 0 1 / 2 1 / 3 0 0 1 / 2 1 / 3 1 / 2 0 0 ] [ 1 / 4 1 / 4 1 / 4 1 / 4 ] = [ 9 / 24 5 / 24 5 / 24 5 / 24 ] w_{1}=\mathrm{M} w_{0}=\left[\begin{array}{cccc}{0} & {1 / 2} & {1} & {0} \\ {1 / 3} & {0} & {0} & {1 / 2} \\ {1 / 3} & {0} & {0} & {1 / 2} \\ {1 / 3} & {1 / 2} & {0} & {0}\end{array}\right]\left[\begin{array}{c}{1 / 4} \\ {1 / 4} \\ {1 / 4} \\ {1 / 4}\end{array}\right]=\left[\begin{array}{c}{9 / 24} \\ {5 / 24} \\ {5 / 24} \\ {5 / 24}\end{array}\right] w1=Mw0=⎣⎢⎢⎡01/31/31/31/2001/2100001/21/20⎦⎥⎥⎤⎣⎢⎢⎡1/41/41/41/4⎦⎥⎥⎤=⎣⎢⎢⎡9/245/245/245/24⎦⎥⎥⎤
然后我们再用转移矩阵乘以 得到 结果，直到第 n 次迭代后 影响力不再发生变
化，可以收敛到 (0.3333，0.2222，0.2222，0.2222），也就是对应着 A、B、C、D 四个页面最终稳定状态下的影响力。
你能看出 A 页面相比于其他页面来说权重更大，也就是 PR 值更高。而 B、C、D 页面的PR 值相等。
- 但公式(1)可能会面临两个问题：
-
- 等级泄露（Rank Leak）：如果一个网页没有出链，就像是一个黑洞一样，吸收了其他
网页的影响力而不释放，最终会导致其他网页的 PR 值为 0。
- 等级泄露（Rank Leak）：如果一个网页没有出链，就像是一个黑洞一样，吸收了其他
-
- 等级沉没（Rank Sink）：如果一个网页只有出链，没有入链（如下图所示），计算的
过程迭代下来，会导致这个网页的 PR 值为 0（也就是不存在公式中的 V）。
针对等级泄露和等级沉没的情况，我们需要灵活处理。
比如针对等级泄露的情况，我们可以把没有出链的节点，先从图中去掉，等计算完所有节点的 PR 值之后，再加上该节点进行计算。不过这种方法会导致新的等级泄露的节点的产生，所以工作量还是很大的。
有没有一种方法，可以同时解决等级泄露和等级沉没这两个问题呢？
公式(2)就可以解决这个问题
- 等级沉没（Rank Sink）：如果一个网页只有出链，没有入链（如下图所示），计算的
-
- 公式(2)计算例子:
PageRank 的随机浏览模型
为了解决简化模型中存在的等级泄露和等级沉没的问题，拉里·佩奇提出了PageRank 的随机浏览模型。他假设了这样一个场景：用户并不都是按照跳转链接的方式来上网，还有一种可能是不论当前处于哪个页面，都有概率访问到其他任意的页面，比如说用户就是要直接输入网址访问其他页面，虽然这个概率比较小。所以他定义了阻尼因子 d，这个因子代表了用户按照跳转链接来上网的概率，通常可以取一个固定值 0.85，而 1-d=0.15 则代表了用户不是通过跳转链接的方式来访问网页的，比如直接输入网址。
P R ( u ) = 1 − d N + d ∑ ν ∈ B u P R ( v ) L ( v ) P R(u)=\frac{1-d}{N}+d \sum_{\nu \in \mathcal{B}_{u}} \frac{P R(v)}{L(v)} PR(u)=N1−d+dν∈Bu∑L(v)PR(v)
其中 N 为网页总数，这样我们又可以重新迭代网页的权重计算了，因为加入了阻尼因子d，一定程度上解决了等级泄露和等级沉没的问题。通过数学定理（这里不进行讲解）也可以证明，最终 PageRank 随机浏览模型是可以收敛
的，也就是可以得到一个稳定正常的 PR 值。- 公式用矩阵来表示，就是这样的一个线性代数的等式:
R = [ ( 1 − q ) / N ( 1 − q ) / N ⋮ ( 1 − q ) / N ] + q [ ℓ ( p 1 , p 1 ) ℓ ( p 1 , p 2 ) ⋯ ℓ ( p 1 , p N ) ℓ ( p 2 , p 1 ) ⋱ ⋮ ℓ ( p i , p j ) ℓ ( p N , p 1 ) ℓ ( p N , p N ) ] R ( 3 ) \mathbf{R}=\left[\begin{array}{c}{(1-q) / N} \\ {(1-q) / N} \\ {\vdots} \\ {(1-q) / N}\end{array}\right]+q\left[\begin{array}{ccc}{\ell\left(p_{1}, p_{1}\right)} & {\ell\left(p_{1}, p_{2}\right)} & {\cdots} & {\ell\left(p_{1}, p_{N}\right)} \\ {\ell\left(p_{2}, p_{1}\right)} & {\ddots} & {} \\ {\vdots} & {} & {\ell\left(p_{i}, p_{j}\right)} & {} \\ {\ell\left(p_{N}, p_{1}\right)} & {} & {} & {\ell\left(p_{N}, p_{N}\right)}\end{array}\right] \mathbf{R} (3) R=⎣⎢⎢⎢⎡(1−q)/N(1−q)/N⋮(1−q)/N⎦⎥⎥⎥⎤+q⎣⎢⎢⎢⎡ℓ(p1,p1)ℓ(p2,p1)⋮ℓ(pN,p1)ℓ(p1,p2)⋱⋯ℓ(pi,pj)ℓ(p1,pN)ℓ(pN,pN)⎦⎥⎥⎥⎤R(3)
(3)中
R = [ PageRank ( p 1 ) PageRank ( p 2 ) ⋮ P a g e Rank ( p N ) ] \mathbf{R}=\left[\begin{array}{c}{\operatorname{PageRank}\left(p_{1}\right)} \\ {\operatorname{PageRank}\left(p_{2}\right)} \\ {\vdots} \\ {\operatorname{Page\operatorname{Rank}}\left(p_{N}\right)}\end{array}\right] R=⎣⎢⎢⎢⎡PageRank(p1)PageRank(p2)⋮PageRank(pN)⎦⎥⎥⎥⎤
是PR值的特征向量
q为阻尼系数
[ ℓ ( p 1 , p 1 ) ℓ ( p 1 , p 2 ) ⋯ ℓ ( p 1 , p N ) ℓ ( p 2 , p 1 ) ⋱ ⋮ ℓ ( p i , p j ) ℓ ( p N , p 1 ) ℓ ( p N , p N ) ] \left[\begin{array}{cccc}{\ell\left(p_{1}, p_{1}\right)} & {\ell\left(p_{1}, p_{2}\right)} & {\cdots} & {\ell\left(p_{1}, p_{N}\right)} \\ {\ell\left(p_{2}, p_{1}\right)} & {\ddots} & {} & {} \\ {\vdots} & {} & {\ell\left(p_{i}, p_{j}\right)} & {} \\ {\ell\left(p_{N}, p_{1}\right)} & {} & {} & {\ell\left(p_{N}, p_{N}\right)}\end{array}\right] ⎣⎢⎢⎢⎡ℓ(p1,p1)ℓ(p2,p1)⋮ℓ(pN,p1)ℓ(p1,p2)⋱⋯ℓ(pi,pj)ℓ(p1,pN)ℓ(pN,pN)⎦⎥⎥⎥⎤
- 公式用矩阵来表示，就是这样的一个线性代数的等式:
是转移矩阵M
ε ( p 1 , p 2 ) \varepsilon\left(p_{1}, p_{2}\right) ε(p1,p2)的定义为对于所有指向了节点i的其它节点
{ ∑ j = 1 n ε ( p i , p j ) = 1 ε ( p x , p y ) = 0 \left\{\begin{array}{c}{\sum_{j=1}^{n} \varepsilon\left(p_{i}, p_{j}\right)=1} \\ {\varepsilon\left(p_{x}, p_{y}\right)=0}\end{array}\right. {∑j=1nε(pi,pj)=1ε(px,py)=0
如果节点j并不指向i ε ( p x , p y ) = 0 \varepsilon\left(p_{x}, p_{y}\right)=0 ε(px,py)=0
即初始 PR 值全部设为 1/n然后把结果带回来反复迭代，直到
R − R ′ < ε R-R^{\prime}<\varepsilon R−R′<ε
得到结点的最终稳定PR值结果
关于我对PageRank 的其它应用的思考
- PageRank 在社交影响力评估中的应用网页之间会形成一个网络，是我们的互联网，论文之间也存在着相互引用的关系，可以说我们所处的环境就是各种网络的集合。
- 只要是有网络的地方，就存在出链和入链，就会有 PR 权重的计算，也就可以运用 PageRank 算法。
- 我们可以把 PageRank 算法延展到社交网络领域中。
比如计算一个人的微博影响力等。它也告诉我们，在社交网络中，链接的质量非常重要。一个人的微博粉丝数并不一定等于他的实际影响力。如果按照 PageRank 算法，还需要看这些粉丝的质量如何。如果有很多明星或者大 V 关注，那么这个人的影响力一定很高。如果粉丝是通过购买僵尸粉得来的，那么即使粉丝数再多，影响力也不高。 - 同样，在工作场景中，比如说脉脉这个社交软件，它计算的就是个人在职场的影响力。如果你的工作关系是李开复、江南春这样的名人，那么你的职场影响力一定会很高。反之，如果你是个学生，在职场上被链入的关系比较少的话，职场影响力就会比较低。同样，如果你想要看一个公司的经营能力，也可以看这家公司都和哪些公司有合作。如果它合作的都是世界 500 强企业，那么这个公司在行业内一定是领导者，如果这个公司的客户都是小客户，即使数量比较多，业内影响力也不一定大。除非像淘宝一样，有海量的中小客户，最后大客户也会找上门来寻求合作。所以权重高的节点，往往会有一些权重同样很高的节点在进行合作。
- 把影响力转化为每日使用时间考虑。
在感兴趣的人或事身上投入了相对多的时间。对其相关的人事物也会投入一定的时间。那个人或事，被关注的越多，它的影响力/受众也就越大。而每个人的时间有限，一般来说每个人最多与150人保持联系，相当于最多有150个出链。但其中一部分人，没人关注，只有出链没有入链，他们就需要社会最低限度的关照。
PageRank 给我们带来的启发
- PageRank 可以说是 Google 搜索引擎重要的技术之一，在 1998 年帮助 Google 获得了搜索引擎的领先优势，现在 PageRank 已经比原来复杂很多，但它的思想依然能带给我们很多启发。
- 比如，如果你想要自己的媒体影响力有所提高，就尽量要混在大 V 圈中；如果想找到高职位的工作，就尽量结识公司高层，或者认识更多的猎头，因为猎头和很多高职位的人员都有链接关系。
- 同样，PageRank 也可以帮我们识别链接农场。链接农场指的是网页为了链接而链接，填充了一些没有用的内容。这些页面相互链接或者指向了某一个网页，从而想要得到更高的权重。
总结
原始PageRank模型中存在的等级泄露和等级沉没这两个问题，PageRank 的随机浏览模型引入了阻尼因子 d 来解决。
算法实现
PageRank 算法工具在 sklearn 中并不存在，我们需要找到新的工具包。实际上有一个关于图论和网络建模的工具叫 NetworkX，它是用 Python 语言开发的工具，内置了常用的图与网络分析算法，可以方便我们进行网络数据分析。
使用时只需
pip install networkx
我写的一个应用案例:
https://github.com/WangZeling/Zhihu_PageRank