matlab双极性二进制基带传输系统的仿真和误码性能验证实践--总结（附代码）

 

        目   录

1.课程设计目的 3

2.使用平台和课程知识 3

3.课程设计题目描述和要求 3

4.课程设计报告内容 4

5.仿真结果分析和结论 7

6．心得体会 7

 

一、课程设计目的：

1. MATLAB是matrix&laboratory两个词的组合，意为矩阵工厂（矩阵实验室），主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中通过该实践，希望同学们掌握对于matlab工具的掌握以及如何仿真的用法。

2.该实践同时涉及《MATLAB及其应用》、《信息论与编码》、《通信原理》三门专业课的知识结合，通过该仿真实践得以验证三门学科中相互交织的一个实验题目，即通过matlab仿真双极性二进制基带传输系统，对于专业问题能够形象体会，并能举一反三。

3.通过实践训练，加强同学们对于计算机程序语言设计、调试能力，专业知识的理解和掌握程度 ，并加强同学们的耐心和细心。

 

二、使用平台和课程知识：

使用平台：MATLAB

   参考课程：《MATLAB及其应用》

《信息论与编码》

《通信原理》

 

• 课程设计题目描述和要求：

1. 题目：双极性二进制基带传输系统的仿真和误码性能验证

2.题目描述：该实践使用基带来传输双极性二进制信号，因此我们在设计系统的时候不用经过调制，编码方式可选择线性分组码、汉明码和卷积码等，这里我们选择用线性分组码来编码和解码，对于系统的性能情况，我们通过统计解码前的误码率和解码后的误码率加以比较，从而得出系统性能的情况。

3.要求：

（1）发送信号的星座图， 发送和接收信号的波形， 不同信噪比情况下， 接收信号的星座图
（2）画出无信道编码时， 误比特率的理论曲线和仿真曲线， 以及有信道编码时误比特率的仿真曲线

（3）解释以上获得的各种结果的合理性
（4）选做：选用不同纠错能力的信道编码方法，比较信道译码后的误码率

四、课程设计报告内容

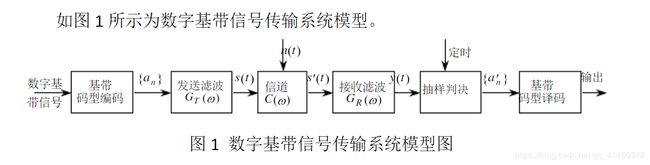
    4.1 双极性二进制基带传输系统的传输模型

    4.2 双极性二进制基带传输系统的仿真框图和程序流程图

 

                 

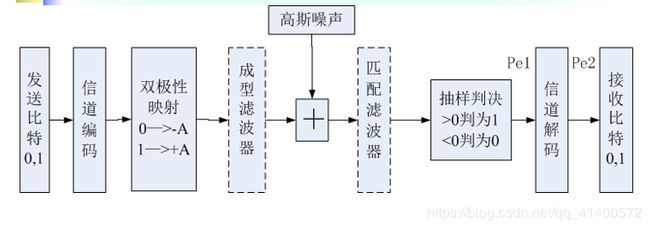
                  图2 双极性二进制基带传输系统框图

                         

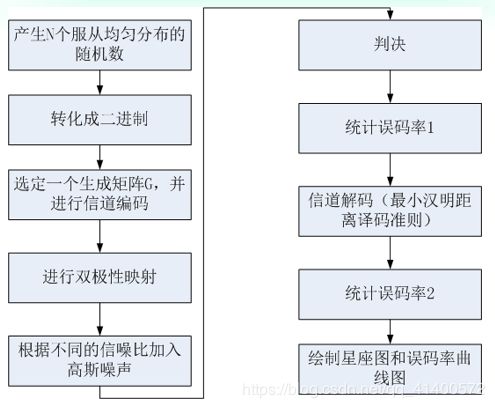
                  图3 双极性二进制基带传输系统程序流程图

 

    4.3 星座图的绘制

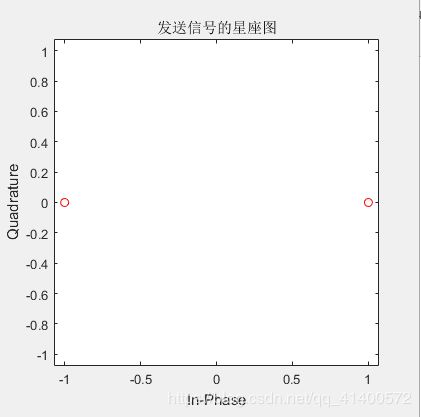
绘制方法：通过双极性映射后打印出发送信号的星座图。

scatterplot(Bipolar_signal,1,0,'ro');

hold on;

title('发送信号的星座图');

之后通过设置不同SNR，加入高斯信号后可以打印出接收信号的星座图。

scatterplot(Gaus_noise_signal,1,0,'ro');

hold on;

title('接收信号的星座图（xdB）');

 

 

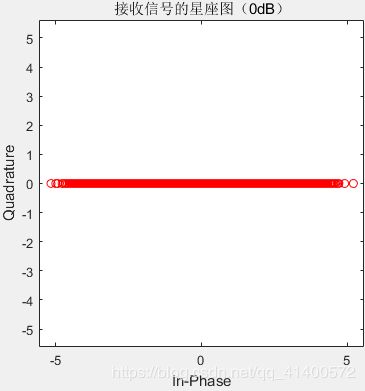
                     图4.3.1 发送信号的星座图                      图4.3.2 接收信号的星座图（0dB）

 

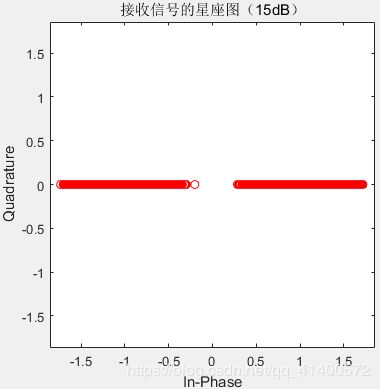
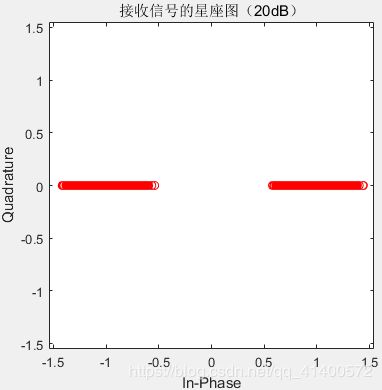
图4.3.3 接收信号的星座图（15dB）                     图4.3.2 接收信号的星座图（20dB）

 

4.4 发送和接收波形的绘制

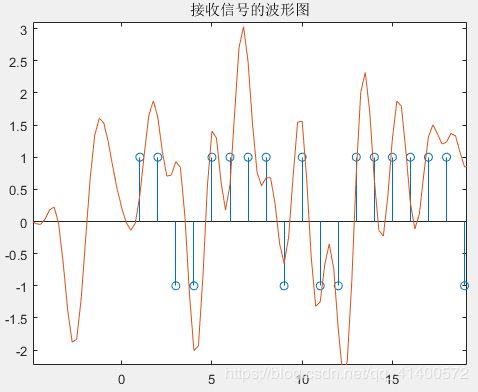
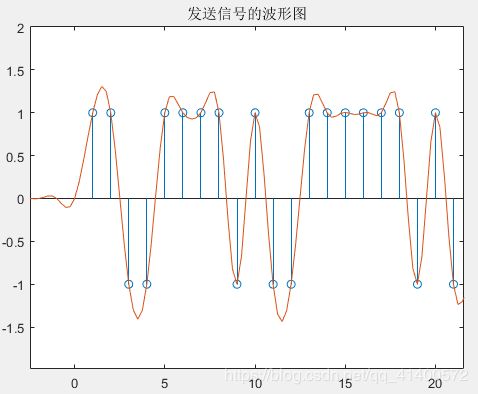
    图4.4.1 发送信号波形                                                                              图4.4.2 接收信号波形（0dB）

  

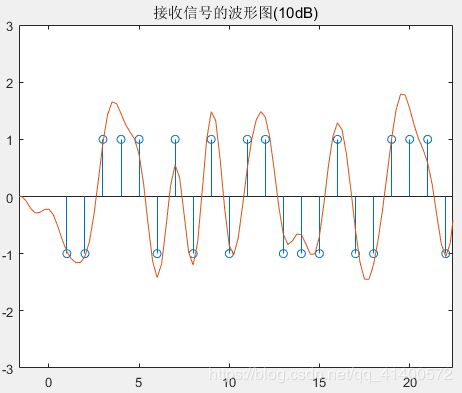
          图4.4.3 接收信号波形（10dB）                                             图4.4.4 接收信号波形（20dB）

 

    4.5 误码率曲线的绘制

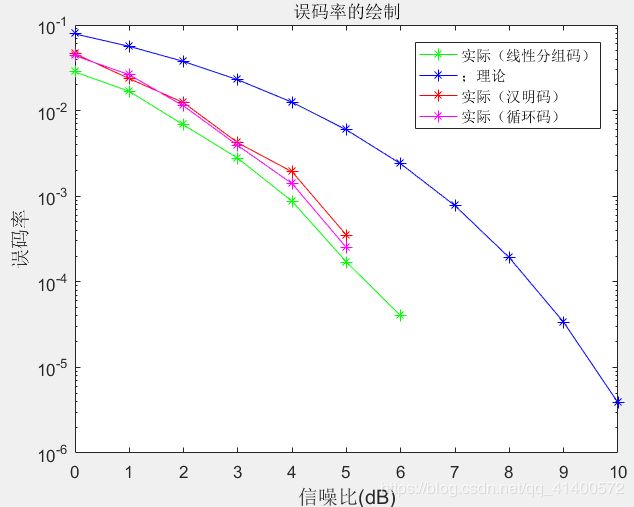
图4.5.1 线性分组码和无编码误码率  

   

    4.6选做部分

 

图4.5.2 加入汉明码和循环码比较

 

五、仿真结果分析和结论

    1.在4.3 星座图的仿真中，我们看到发送端的星座图只有两个点，但其实发送端的信号并不止两个，而是有足够多个，但是由于发送端信号属于双极性信号，因此在星座图中分布于两边重合，而接收端信号则是由许多经过成型滤波器，高斯白噪声，匹配滤波器和抽样之后形成的信号，其数值并不相同，且随着SNR越高，其误码率越低，因此越接近发送端的星座图，故仿真正确。

    2.在4.4发送和接收波形仿真中，可以看出发送端成型波形完整地对应了发送信号，而对比发送端和接收端，可以看出接受信号由于受到可噪声干扰，从而其抽样点并没有和发送端一致，但随着SNR提高，其一致性也在逐渐增大。

    3.在4.5误码率的仿真中，可以看出，有编码的码字具有纠错能力，因此能够纠正一部分码字，误码率比无编码的时候会下降。汉明码和循环码的纠错能力差不多，这是因为此时汉明码作为一种特殊的循环码，二者纠错能力一致故能够实现一样误码率。

 

六、心得体会

    通过本次实验，我加深了对于双极性二进制基带传输系统的认识，将通信原理理论课程学习的知识充分应用在了这次实践中，包括了成型滤波器的设计应使用升余弦滤波器，从而能够增大信号带宽（这是由于信号的相位会顺势跳变），消除码间串扰，高斯噪声的加入和应用，以及匹配滤波器的选择并不是为了进一步消除码间串扰，而是最大程度地使抽样时刻的SNR达到最大。

    对于matlab工具的应用充分提升了我对于matlab的认识与技能娴熟能力，在这期间我不仅掌握了如何通过流程框图一步一步地进行编程，也掌握了对于各个函数的应用，如高斯噪声函数与误码率的统计函数等，同时对于绘图工具也有了极大的认识和掌握，这次实践使我对于之前学习的matlab知识有了进一步的温习和掌握。

    与此同时在信道编码和解码这一部分，我通过对于信息论书籍的学习和掌握，选用了线性分组码作为这次信道编码和解码的载体。对于编码部分，只需要一个mod函数便可实现，但对于解码部分较为复杂。通过理论分析，我成功编写出了解码函数，并加以封装。

    最后，这次实践是一次十分可贵的实践，大大提升了我的理论能力和实践能力。

 

【参考书目】

［1］  樊昌信、曹丽娜，《通信原理（第7版）》，国防工业出版社，2018.7
［2］  曹雪虹、张宗橙，《信息论与编码（第3版）》，清华大学出版社，2016.6

 

附录

1.主函数：

clc;

clear;

close all;

signal_num=40000;%产生随机码字的数目

theory_SNR=0:10;  %信噪比设定

S_N=10.^(theory_SNR./10);  %通过信噪比转换为信号噪声功率比

simu_SNR=10*log10(2.*S_N);   %符号信噪比和比特信噪比的转换

span=8;

sps=4;

beta=0.5;

N2=0:100000/400028:100000;

 

random_mat=rand(signal_num/2,2);   %二极性信号产生

trans_binary(random_mat(:,1)>0.5,1)=1;

trans_binary(random_mat(:,1)<=0.5,1)=0;

trans_binary(random_mat(:,2)>0.5,2)=1;

trans_binary(random_mat(:,2)<=0.5,2)=0;

hamming_binary=reshape(trans_binary,signal_num/4,4); %汉明码输入矩阵

cycle_binary=hamming_binary; %循环码输入矩阵

 

line_Code=line_encoder(trans_binary);  %开始（5,2）线性分组码编码

hamming_code=encode(hamming_binary,7,4,'hamming');%开始（7,4）汉明码编码

cycle_code=encode(hamming_binary,7,4,'cyclic');%开始（7,4）循环码编码

 

Bipolar_signal(line_Code==0)=-1;   %形成线性分组码Bipolar_signal:双极性信号

Bipolar_signal(line_Code==1)=1;

Bipolar_signal_1(hamming_code==0)=-1;   %形成汉明码Bipolar_signal:双极性信号

Bipolar_signal_1(hamming_code==1)=1;

Bipolar_signal_2(cycle_code==0)=-1;   %形成循环码Bipolar_signal:双极性信号

Bipolar_signal_2(cycle_code==1)=1;

 

SNR=20;

%成形滤波器+绘制发送信号的波形图

b=rcosdesign(beta,span,sps,'sqrt');

b_1=rcosdesign(beta,span,sps,'sqrt');

send_signal=upfirdn(Bipolar_signal,b,sps);

hamming_send_signal=upfirdn(Bipolar_signal_1,b,sps);

cycle_send_signal=upfirdn(Bipolar_signal_2,b,sps);

% stem(Bipolar_signal);

% hold on;

% send_plot_signal=filter(b,1,send_signal);

% plot(N2-7,send_plot_signal);

% title('发送信号的波形图');

%

% Gaus_noise_signal=awgn(send_signal,20); %加入高斯噪声信号 

% %匹配滤波器+绘制接收信号的波形图

% receive_signal=filter(b,1,Gaus_noise_signal);

% receive_signal=receive_signal(span*sps+1:sps:end);

% % figure;

% % stem(Bipolar_signal);

% % hold on;

% % plot(N2-7,receive_signal);

% % title('接收信号的波形图');

%

% %发送信号的星座图send_signal

% scatter_plot(Bipolar_signal);

% title('发送信号的星座图');

% hold on;

%

% % 接受信号的星座图

% scatter_plot(receive_signal);

% title('接收信号的星座图');

% hold on;

 

for SNR=0:1:10

    Gaus_noise_signal=awgn(send_signal,simu_SNR(SNR+1)); %线性分组码加入高斯噪声信号 

    hamming_gaus=awgn(hamming_send_signal,simu_SNR(SNR+1)); %汉明码加入高斯噪声信号

    cycle_gaus=awgn(cycle_send_signal,simu_SNR(SNR+1)); %循环码加入高斯噪声信号

    %匹配滤波器+绘制接收信号的波形图+抽样

    receive_signal=filter(b,1,Gaus_noise_signal);

    hamming_receive_signal=filter(b_1,1,hamming_gaus);

    cycle_receive_signal=filter(b_1,1,cycle_gaus);

    %抽样判决

    receive_signal=receive_signal(span*sps+1:sps:end);

    hamming_receive_signal=hamming_receive_signal(span*sps+1:sps:end);

    cycle_receive_signal=cycle_receive_signal(span*sps+1:sps:end);

    judge_signal(receive_signal>0)=1;

    judge_signal(receive_signal<=0)=0;

    judge_signal_1(hamming_receive_signal>0)=1;

    judge_signal_1(hamming_receive_signal<=0)=0;

    judge_signal_2(cycle_receive_signal>0)=1;

    judge_signal_2(cycle_receive_signal<=0)=0;

    hamming_signal=reshape(judge_signal_1,10000,7);

    cycle_signal=reshape(judge_signal_2,10000,7);

   

    %解码程序

    judge_signal=reshape(judge_signal,20000,5);

    C=line_decoder(judge_signal);%线性分组码解码

    hamming_decode=decode(hamming_signal,7,4,'hamming');%汉明码解码

    cycle_decode=decode(cycle_signal,7,4,'cyclic');%循环码解码

    %误码率的统计

    [num,err]=biterr(cycle_binary,cycle_decode); %统计循环码的误码率

    [M,q]=biterr(hamming_binary,hamming_decode); %统计汉明码的误码率

    [N,p]=biterr(line_Code,C); %统计经过线性分组码的误码率

   

    simu(SNR+1)=err;

    simu_err_rate(SNR+1)=p;

    simu_err_rate_out(SNR+1)=q;

    theory_err_rate(SNR+1)=0.5*erfc(sqrt(S_N(SNR+1)));%理论误码率

end

figure;

semilogy(theory_SNR,simu_err_rate,'g-*',theory_SNR,theory_err_rate,'b-*',theory_SNR,simu_err_rate_out,'r-*',theory_SNR,simu,'m-*');

title('误码率的绘制');

legend('实际（线性分组码）','；理论','实际（汉明码）','实际（循环码）');

xlabel('信噪比(dB)','FontSize',12);

ylabel('误码率','FontSize',12);

 

2.线性分组码编码解码程序：

编码：function R=line_encoder(m)

%(5,2)线性分组码编码

G=[1,0,1,1,1;

   0,1,1,0,1];%生成矩阵

R=m*G;

R=mod(R,2);

 

解码：function C = line_decoder( R )

%（5,2）线性分组码解码

H=[1,1,1,0,0;

   1,0,0,1,0;

   1,1,0,0,1];%校验矩阵

S=mod(R*H',2);

S=4.*S(:,1)+2.*S(:,2)+S(:,3);

row=find(S~=0);

[a,b]=size(row);

for i=1:a

    switch(S(row(i)))

        case{1}

            R(row(i),:)=mod(R(row(i),:)+[0,0,0,0,1],2);

        case{2}

            R(row(i),:)=mod(R(row(i),:)+[0,0,0,1,0],2);

        case{3}

            R(row(i),:)=mod(R(row(i),:)+[0,0,0,1,1],2);

        case{4}

            R(row(i),:)=mod(R(row(i),:)+[0,0,1,0,0],2);

        case{5}

            R(row(i),:)=mod(R(row(i),:)+[0,1,0,0,0],2);

        case{6}

            R(row(i),:)=mod(R(row(i),:)+[0,0,1,1,0],2);

        case{7}

            R(row(i),:)=mod(R(row(i),:)+[1,0,0,0,0],2);

    end

end

C=R;