C语言实现Dijkstra算法（求解两点之间最短路径问题）

含有约束条件下的最短路径问题

C语言实现最优路径算法（有限时间约束条件下的算法模型）

程序框图及变量说明

程序框图

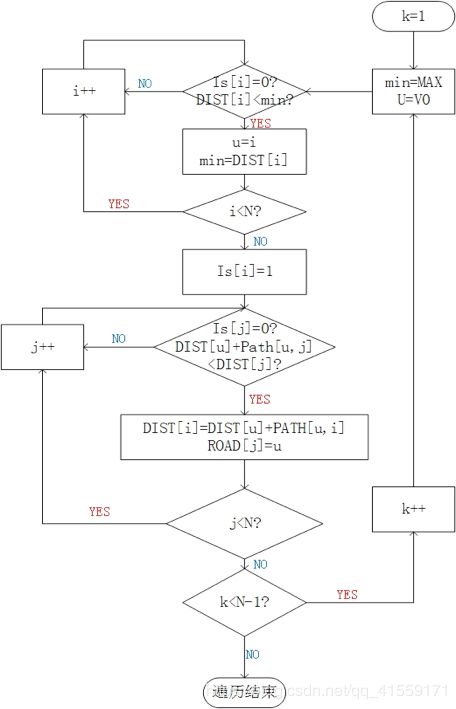
常量：
N——所选节点个数
MAX——定义两点之间若无路径赋予的最大值

变量：
DIST[N]——存储已经搜寻到的最短路径
Is[N]——存储节点是否被遍历的状态
Path[N]——图之间的路径矩阵
Road[N]——存储最短路径时该节点的上一节点

算法解释

该程序遍历N个点，故总遍历次数应为N-1
第一个循环为标点：找到未标注点中距离起点最小的点将其标号；
第二个循环为更新未标注点到起点的最短路径：基于第一个循环新标出的点，更新余下点中的最短路径。直到遍历到终点程序结束。

所用数据

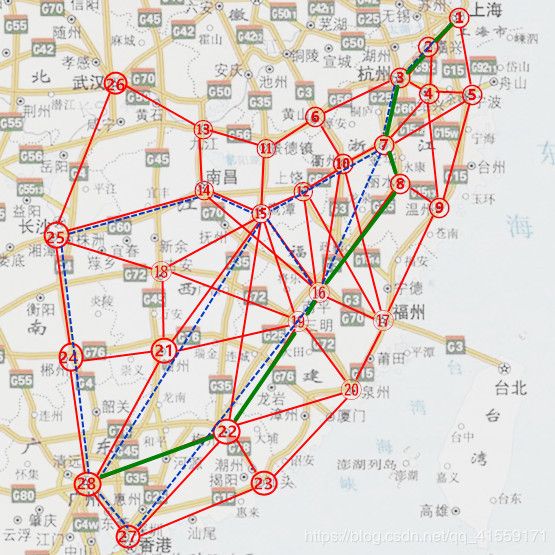
这是上海到广州中28个城市之间的公路距离，在这里拟求上海到广州之间的最短路径

代码实现

#include 
//假设取10个节点，N=28
//定义无穷大为100000
#define N 28
double distance[N];//最短路径
int path[N];//上一节点
int is[N];//是否选用该节点,0位未选用
double destination[N][N]={
    {0,    97.9,    100000,    100000,    227.2,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//1
    {97.9,    0,    84.5,    106.1,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//2
    {100000,    84.5,    0,    56.7,    100000,    221.4,    176.3,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//3
    {100000,    106.1,    56.7,    0,    121.2,    100000,    164.1,    100000,    276.6,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//4
    {100000,    100000,    100000,    121.2,    0,    100000,    244.2,    100000,    273,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//5
    {100000,    100000,    100000,    100000,    100000,    0,    100000,    100000,    100000,    143.7,    166.5,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//6
    {100000,    100000,    100000,    100000,    244.2,    100000,    0,    116.6,    100000,    96.5,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//7
    {100000,    100000,    100000,    100000,    100000,    100000,    116.6,    0,    129.7,    100000,    100000,    100000,    100000,    100000,    100000,    201.7,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//8
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    129.7,    0,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    318.3,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//9
    {100000,    100000,    100000,    100000,    100000,    143.7,    96.5,    100000,    100000,    0,    100000,    120.3,    100000,    100000,    100000,    350.5,    467.9,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//10
    {100000,    100000,    100000,    100000,    100000,    166.5,    100000,    100000,    100000,    100000,    0,    100000,    144,    100000,    159.3,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//11
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    120.3,    100000,    0,    100000,    100000,    103.8,    266.3,    383.7,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//12
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    144,    100000,    0,    130,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    242,    100000,    100000},//13
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    130,    0,    161.1,    420.3,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    347.2,    100000,    100000,    100000},//14
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    159.3,    103.8,    100000,    161.1,    0,    328.8,    100000,    282.5,    338,    100000,    434.1,    555,    100000,    100000,    100000,    100000,    100000,    100000},//15
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    350.5,    100000,    266.3,    100000,    420.3,    328.8,    0,    180,    100000,    82.9,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//16
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    318.3,    467.9,    100000,    383.7,    100000,    100000,    100000,    180,    0,    100000,    100000,    182,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000},//17
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    282.5,    100000,    100000,    0,    395.9,    100000,    190.5,    100000,    100000,    397.8,    100000,    100000,    100000,    100000},//18
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    338,    82.9,    100000,    395.9,    0,    276.9,    378.6,    324.8,    100000,    100000,    100000,    100000,    100000,    100000},//19
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    182,    100000,    276.9,    0,    100000,    389.3,    329.4,    100000,    100000,    100000,    100000,    100000},//20
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    434.1,    100000,    100000,    190.5,    378.6,    100000,    0,    100000,    100000,    246.9,    100000,    100000,    100000,    418.6},//21
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    555,    100000,    100000,    100000,    324.8,    389.3,    100000,    0,    157.7,    100000,    100000,    100000,    364.5,    388.1},//22
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    329.4,    100000,    157.7,    0,    100000,    100000,    100000,    333.7,    100000},//23
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    397.8,    100000,    100000,    246.9,    100000,    100000,    0,    317.7,    100000,    100000,    367.6},//24
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    317.7,    0,    345.8,    100000,    100000},//25
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    242,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    345.8,    0,    100000,    100000},//26
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    364.5,    333.7,    100000,    100000,    100000,    0,    135.6},//27
    {100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    100000,    418.6,    388.1,    100000,    367.6,    100000,    100000,    135.6,    0}//28

};//路程矩阵
//find函数寻找最短路径
void find(){
    //最多进行N-1次循环
    for(int k=1;k<N;k++){
        double max=100000;//路径最大值
        int u=0;//u为已经找到最短路径的节点,初始状态都为起点0
        for(int i=0;i<N;i++){
            if(is[i]==0 && distance[i]<max){
                u=i;
                max=distance[i];
            }
        }
        is[u]=1;
        //找出一点后更新其余点的最短路径
        for(int y=0;y<N;y++){
            if(is[y]==0 && distance[u]+destination[u][y]<distance[y]){
                distance[y]=distance[u]+destination[u][y];
                path[y]=u;
            }
        }
    }
}
//输出最短路径
void showpath(){
    for(int i=1;i<N;i++){
        if(is[i]==1){
            int k=i;
            while(k!=0){
                int k2=k+1;//使输出与标号对应
                std::cout<<k2<<"<-";
                k=path[k];
            }//若前一节点不为起点则不断查询前一节点
            std::cout<<1<<' '<<"所用里程为"<<distance[i];
            std::cout<<std::endl;//输出一项最短路径
        }
        else{
            std::cout<<i<<"不能到达";
            std::cout<<std::endl;
        }
    }
}
//主函数起到遍历初始值的效果
int main(){
    //开始时进行初始化遍历
    for(int i=0;i<N;i++){
        path[i]=0;//一开始所有点的前一点为起点
        is[i]=0;//都未选用
        distance[i]=destination[0][i];//初始时路程都为起点道该点距离
    }
    is[0]=1;//第一个节点选用
    find();
    showpath();
}

运行结果

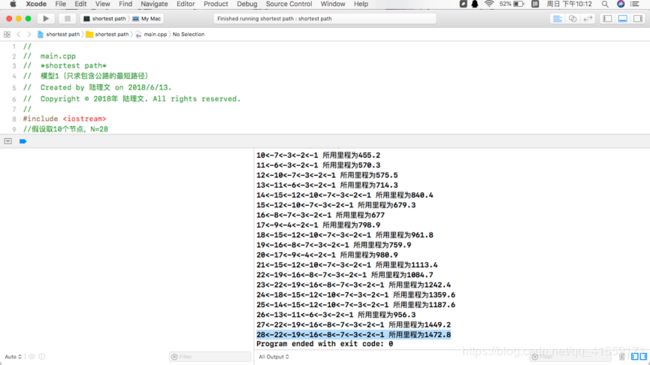
通过网上查询资料可得上海到广州的公路距离为：1435.2，距离相差37.6公里，考虑到误差可能由于所选节点数不够

在地图上标出：