神经网络学习——第一个代码学习
学习的博客来自:人工神经网络——反向传播算法(BP)以及Python实现
一共分为两个py文件
1、BPNN
"""
输入层:3
隐藏层:3
输出层:2
"""
import numpy as np
import math
import matplotlib.pyplot as plt
# 激励函数及相应导数
def sigmoid(x):
return 1.0 / (1 + np.exp(-x))
def diff_sigmoid(x):
fval = sigmoid(x)
return fval * (1 - fval)
def linear(x):
return x
def diff_linear(x):
return np.ones_like(x)
class BP:
def __init__(self, n_hidden=None, f_hidden='sigmoid', f_output='linear',
epsilon=0, maxstep=0, eta=0, alpha=0):
"""
:param n_hidden: 输入层神经元数目
:param f_hidden: 隐藏层神经元数目
:param f_output: 输出层神经元数目
:param epsilon: 阈值
:param maxstep:
:param eta: 学习率
:param alpha: 动量因子
:return:
"""
self.n_input = None
self.n_hidden = n_hidden
self.n_output = None
self.f_hidden = f_hidden
self.f_output = f_output
self.epsilon = epsilon
self.maxstep = maxstep
self.eta = eta
self.alpha = alpha
self.wih = None # 输入层到隐藏层权值矩阵
self.who = None # 隐藏层到输出层权值矩阵
self.bih = None # 输入层到隐藏层阈值
self.bho = None # 隐藏层到输出层阈值
self.N = None
def init_param(self, X_data, y_data):
# 初始化
if len(X_data.shape) == 1: # 若输入数据为一维数组,则进行转置为n维数组
X_data = np.transpose([X_data])
self.N = X_data.shape[0]
# normalizer = np.linalg.norm(X_data, axis=0)
# X_data = X_data / normalizer
if len(y_data.shape) == 1:
y_data = np.transpose([y_data])
self.n_input = X_data.shape[1]
self.n_output = y_data.shape[1]
if self.n_hidden is None:
self.n_hidden = int(math.ceil(math.sqrt(self.n_input + self.n_output)) + 2)
self.wih = np.random.rand(self.n_input, self.n_hidden) # i*h
self.who = np.random.rand(self.n_hidden, self.n_output) # h*o
self.bih = np.random.rand(self.n_hidden) # h
self.bho = np.random.rand(self.n_output) # o
return X_data, y_data
def inspirit(self, name):
# 获取相应的激励函数
if name == 'sigmoid':
return sigmoid
elif name == 'linear':
return linear
else:
raise ValueError('the function is not supported now')
def diff_inspirit(self, name):
# 获取相应的激励函数的导数
if name == 'sigmoid':
return diff_sigmoid
elif name == 'linear':
return diff_linear
else:
raise ValueError('the function is not supported now')
def forward(self, X_data):
# 前向传播
x_hidden_in = np.dot(X_data, self.wih) + self.bih # n*h
x_hidden_out = self.inspirit(self.f_hidden)(x_hidden_in) # n*h
x_output_in = np.dot(x_hidden_out, self.who) + self.bho # n*o
x_output_out = self.inspirit(self.f_output)(x_output_in) # n*o
return x_output_out, x_output_in, x_hidden_out, x_hidden_in
def fit(self, X_data, y_data):
# 训练主函数
X_data, y_data = self.init_param(X_data, y_data)
step = 0
E = np.zeros_like(y_data)
# 初始化动量项
delta_wih = np.zeros_like(self.wih)
delta_who = np.zeros_like(self.who)
delta_bih = np.zeros_like(self.bih)
delta_bho = np.zeros_like(self.bho)
while step < self.maxstep:
step += 1
# 向前传播
x_output_out, x_output_in, x_hidden_out, x_hidden_in = self.forward(X_data)
if np.sum(abs(x_output_out - y_data)) < self.epsilon:
break
# 计算误差函数E = 0.5*(y_data - x_output_out)^2
E = 0.5*(y_data - x_output_out)**2
# 误差反向传播,依据权值逐层计算当层误差
err_output = y_data - x_output_out # n*o, 输出层上,每个神经元上的误差
delta_ho = -err_output * self.diff_inspirit(self.f_output)(x_output_in) # n*o
err_hidden = np.dot(delta_ho, self.who.T) # n*h, 隐藏层(相当于输入层的输出),每个神经元上的误差
# 隐藏层到输出层权值及阈值更新
delta_bho = np.sum(self.eta * delta_ho + self.alpha * delta_bho, axis=0) / self.N
self.bho -= delta_bho
delta_who = np.dot(self.eta * x_hidden_out.T, delta_ho) + self.alpha * delta_who
self.who -= delta_who
# 输入层到隐藏层权值及阈值的更新
delta_ih = err_hidden * self.diff_inspirit(self.f_hidden)(x_hidden_in) # n*h
delta_bih = np.sum(self.eta * delta_ih + self.alpha * delta_bih, axis=0) / self.N
self.bih -= delta_bih
delta_wih = np.dot(self.eta * X_data.T, delta_ih) + self.alpha * delta_wih
self.wih -= delta_wih
return
def predict(self, X):
# 预测
res = self.forward(X)
return res[0]
2、Mytest
"""
Input: 训练数据集X_data和y_data, 神经网络必要参数,误差阈值epsilon,最大迭代次数maxstep
Output: 神经网络权值W
Step1: 初始化权值矩阵W,阈值b
Step2: 迭代训练直到误差小于阈值epsilon或达到最大迭代次数maxstep。训练步骤包括前向传播和误差反向传播。
"""
import matplotlib.pyplot as plt
import numpy as np
import BPNN
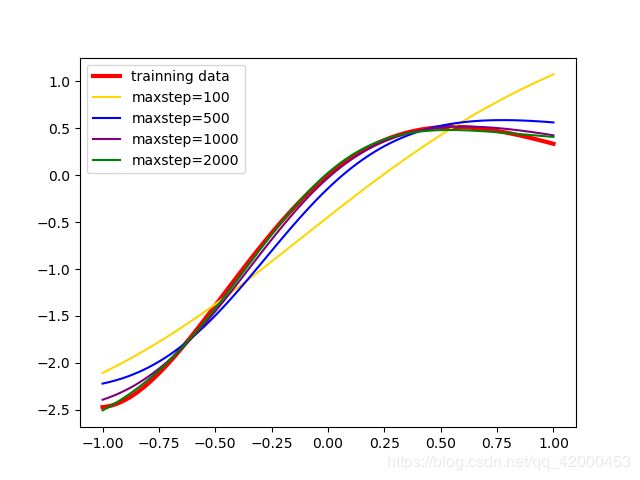
N = 100
X_data = np.linspace(-1, 1, N)
X_data = np.transpose([X_data])
y_data = np.exp(-X_data) * np.sin(2 * X_data)
plt.plot(X_data, y_data, color='red', label='trainning data',linewidth=3)
bp100 = BPNN.BP(n_hidden=None, f_hidden='sigmoid',f_output='linear',
maxstep=100,epsilon=1e-3, eta=0.01, alpha=0.1)
bp100.fit(X_data, y_data)
pred100 = bp100.predict(X_data)
bp500 = BPNN.BP(n_hidden=None, f_hidden='sigmoid',f_output='linear',
maxstep=500,epsilon=1e-3, eta=0.01, alpha=0.1)
bp500.fit(X_data, y_data)
pred500 = bp500.predict(X_data)
bp1000 = BPNN.BP(n_hidden=None, f_hidden='sigmoid',f_output='linear',
maxstep=1000,epsilon=1e-3, eta=0.01, alpha=0.1)
bp1000.fit(X_data, y_data)
pred1000 = bp1000.predict(X_data)
bp2000 = BPNN.BP(n_hidden=None, f_hidden='sigmoid',f_output='linear',
maxstep=2000,epsilon=1e-3, eta=0.01, alpha=0.1)
bp2000.fit(X_data, y_data)
pred2000 = bp2000.predict(X_data)
plt.plot(X_data, pred100, color='gold', label='maxstep=100')
plt.plot(X_data, pred500, color='blue', label='maxstep=500')
plt.plot(X_data, pred1000, color='purple', label='maxstep=1000')
plt.plot(X_data, pred2000, color='green', label='maxstep=2000')
plt.legend()
plt.show()