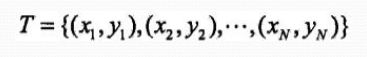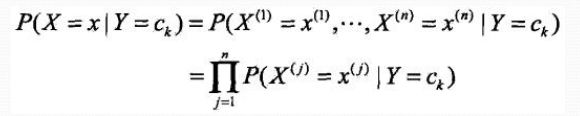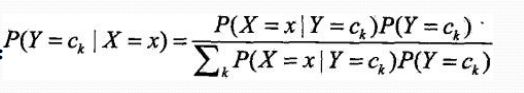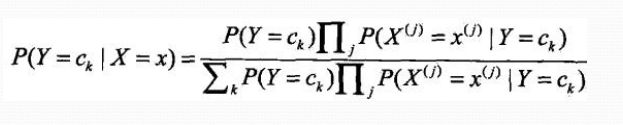深度学习03—朴素贝叶斯决策+股价预测实例

1、贝叶斯决策论

贝叶斯决策论（Bayesian decision theory）是在概率框架下实施决策的基本方法。
在分类问题情况下，在所有相关概率都已知的理想情形下，贝叶斯决策考虑如何基于这些概率和误判损失来选择最优的类别标记。

2、基本方法

训练数据集：

联合分布

朴素贝叶斯通过训练数据集学习联合概率分布P(X,Y)
即先验概率分布：

及条件概率分布：

条件独立性假设

“朴素”贝叶斯名字由来，牺牲分类准确性。

贝叶斯定理

代入上式：

贝叶斯分类器

分母对所有ck都相同：

3、后验概率最大化的含义

朴素贝叶斯法将实例分到后验概率最大的类中，等价于 期望风险最小化
假设选择0-1损失函数：f(X)为决策函数

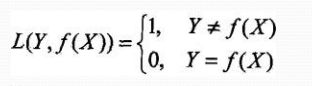
期望风险函数：

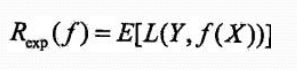
取条件期望：

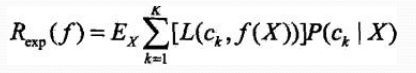
只需对X=x逐个极小化，得：

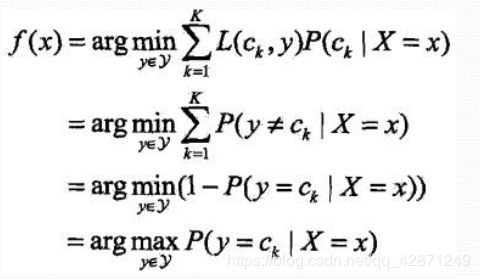
推导出后验概率最大化准则：

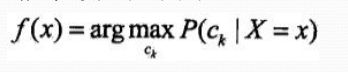
4、股价预测实例

数据准备

利用tuagare接口导入数据以及计算因子的方法这篇博客已经详细介绍了：
https://blog.csdn.net/qq_42871249/article/details/104274239
但对贝叶斯实例的介绍不详细，这里较详细的介绍。
这是整理后的部分数据：y代表第二天股价的涨跌情况，a1,a2,a4分别代表日回报率指标、rsi指标、cci指标。

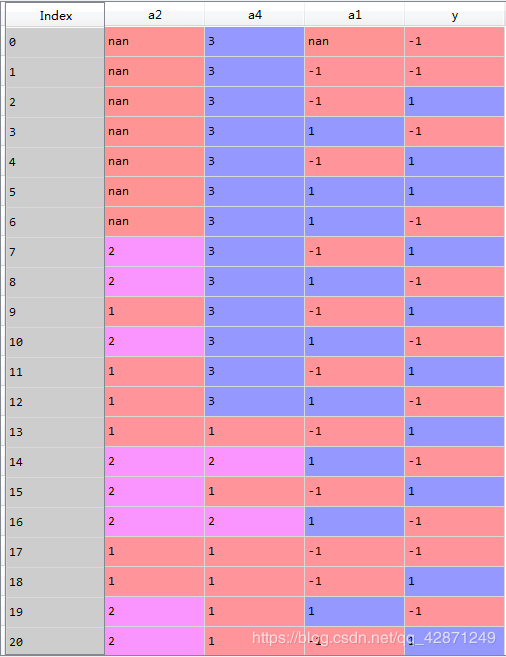
贝叶斯分类器计算概率

根据贝叶斯分类器进行决策：

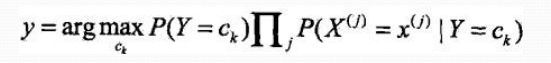
因此要计算训练集的条件概率：
先定义

y_ = [-1,0,1]
a1_ = [-1,0,1]
a2_ = [1,2,3]
a4_ = [1,2,3]
dic = {}

计算变量a1的条件概率：

for i in y_:
    for j in a1_:
        dic['y'+str(i)+'_a1'+str(j)] = sum(
                data['a1'][data['y']==i]==j)/sum(
                        data['y']==i)

看一下结果：

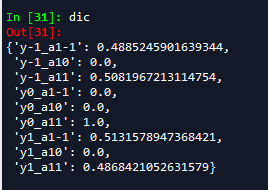
“y-1_a1-1”代表y为-1时a1为-1的概率，其它类似。
同理计算a2,a4的条件概率：

for i in y_:
    for j in a2_:
        dic['y'+str(i)+'_a2'+str(j)] = sum(
                data['a2'][data['y']==i]==j)/sum(
                        data['y']==i)
for i in y_:
    for j in a4_:
        dic['y'+str(i)+'_a4'+str(j)] = sum(
                data['a4'][data['y']==i]==j)/sum(
                        data['y']==i)

结果如下：

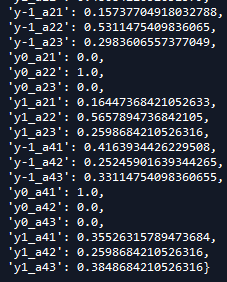
再计算P(Y=-1),P(Y=1),P(Y=0)的概率：

y_ = sum(data['y']==-1)/len(data['y'])
y0 = sum(data['y']==0)/len(data['y'])
y1 = sum(data['y']==1)/len(data['y'])

预测

接下来对如下某个样本进行预测：
原本y的值为-1，a1，a2，a4的值分别为1，2，1

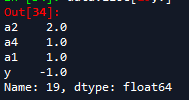
预测

py_ = y_*dic['y-1_a22']*dic['y-1_a41']*dic['y-1_a1-1']
py0 = y0*dic['y0_a22']*dic['y0_a41']*dic['y0_a1-1']
py1 = y1*dic['y1_a22']*dic['y1_a41']*dic['y1_a1-1']

py_、py0、py1分别代表当样本的自变量（即a1，a2，a4分别为1，2，1时）出现这种情况时，因变量y分别为-1,0,1的概率。
计算结果：

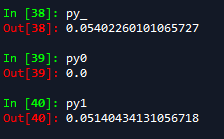
取最大值即y=-1，即股价第二天会下跌，与真实值y也是相符的。

拉普拉斯平滑

目的

在训练集有限的情况下，给定类别，某一特征值出现的条件概率可能为0，这样在贝叶斯公式中分子和分母都为0，为了避免这种情况，就要用到拉普拉斯平滑。

即：在文本分类的问题中，当一个词语没有在训练样本中出现，该词语调概率为0，使用练乘计算文本出现概率时也为0.这是不合理的，不能因为一个事件没有观察到就武断的认为该事件的概率是0.

理论支撑：

为了结局零概率的问题，法国数学家拉普拉斯最早突出用加1的方法估计没有出现过的现象的概率，所以加法平滑也叫做拉普拉斯平滑。

嘉定训练样本很大时，每个分量X的计数加1造成估计概率变化可以忽略不记，但可以方便有效的避免零概率问题。

应用举例

假设在文本分类中，有3个类，C1，C2，C3，在指定的训练样本中，某个词语K1，在各个类中观测计数分别为0，990，10，K1的概率为0，0.99，0.01，对这三个量使用拉普拉斯平滑的计算方法如下：

1/1003=0.001，991/1003=0.922，11/1003=0.011

在实际的使用中也经常使用加lambda(1>=lambda>=0)来代替简单的加1。如果对N个计数都加上lambda,这时分母也要记得加上N*lambda。