网络流(最大流,增广路,为何建反边,Dinic,SAP,二分图匹配,最小割,最大权闭合图)
目录:
最大流
增广路
为何建反边
Dinic
SAP
二分图匹配
最小割
最大权闭合图
备注:(当n>>m时应该用SAP,m>>n时用Dinic.)
最大流
含义:从源点到经过的所有路径的最终到达汇点的所有流量和。(就是水龙头从一个顶点灌水到另一个顶点处水的最大值)
与最大流密切相关的就是增广路了。
增广路的含义:
增广路就是一条从源点到汇点的路,并且带有一个值,表示该增广路的最大流量,该值得大小取决于该增广路中拥有最小流量的边。
大家一同的困惑:建立反边有什么用。
为什么最大流算法要建立反边?
首先有一个这样的图

我们跑一边增广路可以得到A→B→C→D
那么图就变为

但是这很明显不是最大流,最大流应该为2
所以我们得有反悔的机会,所以要建反边,如图
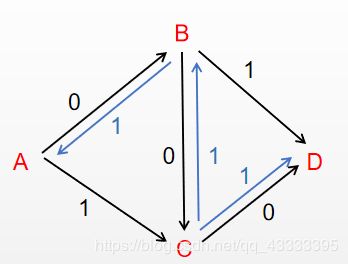
这时候再找一次增广路可以找到A→C→B→D。(A→C和B→D)
此时由于我们跑了一遍B到C的反边,所以最开始的那条增广路A→B→C→D就会被分为A→B和C→D,再与最新找到的增广路相结合就有两条增广路
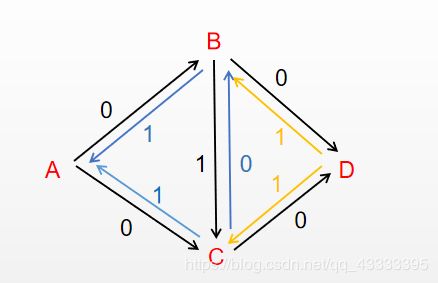
A→B→D
A→C→D
最大流为两条橙色的反边的和。
所以说如果新的增广路跑了反边,证明不使用那条路的反边大小的流,并且与前面新的路相结合形成新的两条路。(重点:不使用跑了反边的流)
Dinic算法的大致步骤
1、建立网络(包括正向弧和反向弧(初始边权为0)),将总流量置为0
void addedge(int u, int v, int c) {
edge[edn].u = u;
edge[edn].v = v;
edge[edn].c = c;
edge[edn].next = p[u];
p[u] = edn++;
edge[edn].u = v;
edge[edn].v = u;
edge[edn].c = 0;
edge[edn].next = p[v];
p[v] = edn++;
}
2、构造层次网络
简单的说,就是 求出每个点u的层次 ,u的层次是从源点到该点的最短路径(注意:这个最短路是指弧的权都为1的情况下的最短路),若与源点不连通,层次置为 -1
一遍BFS轻松解决
int bfs() {
queue<int> q;
memset(d, -1, sizeof(d));
d[sp] = 0;
q.push(sp);
while (!q.empty()) {
int cur = q.front();
q.pop();
for (int i = p[cur]; i != -1; i = edge[i].next) {
int u = edge[i].v;
if (d[u] == -1 && edge[i].c > 0) {
d[u] = d[cur] + 1;
q.push(u);
}
}
}
return d[tp] != -1;
}
3、判断汇点的层次是否为-1 (上一步的作用)
是:再见,算法结束,输出当前的总流量
否:下一步
int dinic(int sp, int tp) {
int total = 0, t;
while (bfs()) {
while (t = dfs(sp, MAX))
total += t;
}
return total;
}
4、用一次DFS完成所有增广,增广是什么呢?
增广(我的理解):通过DFS找上述的增广路,找到了之后,将每条边的权都减去该增广路中拥有最小流量的边的流量,将每条边的反向边的权增加这个值,同时将总流量加上这个值
DFS直到找不到一条可行的从原点到汇点的路
int dfs(int a, int b) {
int r = 0;
if (a == tp)
return b;
for (int i = p[a]; i != -1 && r < b; i = edge[i].next) {
int u = edge[i].v;
if (edge[i].c > 0 && d[u] == d[a] + 1) {
int x = min(edge[i].c, b - r);
x = dfs(u, x);
r += x;
edge[i].c -= x;
edge[i ^ 1].c += x;
}
}
if (!r)
d[a] = -2;
return r;
}
5、goto 步骤2
细节处理,如何快速找到一条边的反向边:边的编号从0开始,反向边加在正向边之后,反向边即为该点的编号异或1(偶为正,奇为反,异或可以相反)
int dinic(int sp, int tp) {
int total = 0, t;
while (bfs()) {
while (t = dfs(sp, MAX))
total += t;
}
return total;
}
复杂度: 理论上来说,最慢应该是O((n^2)*m),n表点数,m表边数,实际上呢,应该快得不少
总代码:
#include 先来一道【模板题】
SAP
首先引入几个新名词:
1、距离标号(就是Dinic分层的层数):
所谓距离标号 ,就是某个点到汇点的最少的弧的数量(即边权值为1时某个点到汇点的最短路径长度)。
设点i的标号为level[i],那么如果将满足level[i]=level[j]+1的弧(i,j)叫做允许弧 ,且增广时只走允许弧。(在Dinic也满足)
2、断层(本算法的Gap优化思想):
gap[i]数组表示距离标号为i的点有多少个,如果到某一点没有符合距离标号的允许弧,那么需要修改距离标号来找到增广路; 如果重标号使得gap数组中原标号数目变为0,则算法结束。
SAP算法框架:
1、初始化;
2、不断沿着可行弧找增广路。可行弧的定义为{( i , j ) , level[i]==level[j]+1};
3、当前节点遍历完以后,为了保证下次再来的时候有路可走,重新标号当前距离,level[i]=min(level[j]+1)
该算法最重要的就是gap常数优化了。
#include二分图匹配
离散有学。如图:给你A集合和B集合以及它们的元素之间的关系。
a与z,b与x,b与y,c与y
最大匹配即为(a,z),(b,x),(c,y)
对于二分图我们可以转化为最大流的题目。
但是我们得先建立两个点(源点和汇点)。其次我们建边的容量为1。同时得建立反图。(用来反悔,每次反悔都能变成两个匹配)
如图:
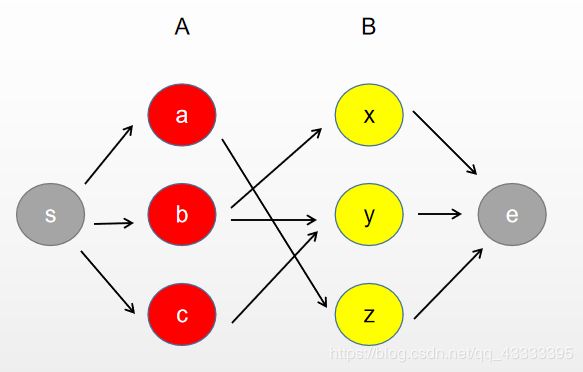
然后跑一边Dinic即可。
关键:最大流就是最大匹配。
代码:
#include 最大匹配数:最大匹配的匹配边的数目
最小点覆盖数:选取最少的点,使任意一条边至少有一个端点被选择
最大独立数:选取最多的点,使任意所选两点均不相连
最小路径覆盖数:对于一个 DAG(有向无环图),选取最少条路径,使得每个顶点属于且仅属于一条路径。路径长可以为 0(即单个点)。
解题的关键:
定理1:最大匹配数 = 最小点覆盖数(这是 Konig 定理)
定理2: **最大点独立数=点的个数-最大匹配(最小点覆盖数) **
定理3:最小路径覆盖数 = 顶点数 - 最大匹配数(最小点覆盖数)
最小割
割的定义:设Ci为网络G中一些弧的集合,若从G中删去Ci中的所有弧能使得从源点Vs到汇点Vt的路集为空集时,称Ci为Vs和Vt间的一个割。(注意,必须是删除Ci中的所有边)
最小割:图中所有的割中,边权值和最小的割为最小割。(即让图中从源点到汇点流量为0)
以下边这个例子来说明最大流和最小割之间的关系:

从1到4,中间经过2,3两节点,问此时的最大流是多少?
首先找一条从1到4的路径[1,2,4],该路径的最大流量是min(2,3)=2,因为[1,2]上面的容量已经被用了,所以路径[1,2,3,4]就行不通了,割去[1,2]后图变成了以下形式:
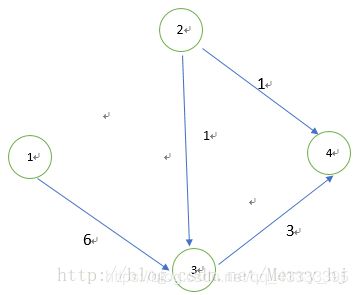
此时再找从1到4的路径[1,3,4],路径的最大流量是min(3,6)=3.割去[b,t]后,图如下:
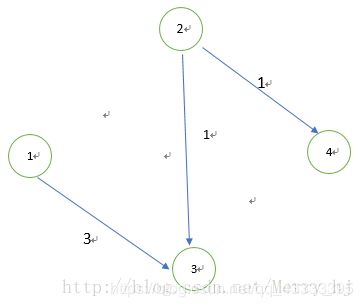
此时就不存在从S到t的可行路径了,则结束最大流的查找。此时的最大流是2+3=5,被割的边容量和是2+3=5,即最大流=最小割。
关键:求最小割就是求最大流。
最大权闭合图:最大权值=正点权之和-最小割
所谓闭合子图就是给定一个有向图,从中选择一些点组成一个点集V。对于V中任意一个点,其后续节点都仍然在V中。比如:

在这个图中有8个闭合子图:∅, {3}, {4}, {2,4}, {3,4}, {1,3,4}, {2,3,4}, {1,2,3,4}
最大权闭合子图即为:在一个图中权值最大的子图;
下面以一道求最大权闭合子图的模板题目为例:
eg:Hiho Coder 1398(求最大权闭合子图)
周末,小Hi和小Ho所在的班级决定举行一些班级建设活动。
根据周内的调查结果,小Hi和小Ho一共列出了N项不同的活动(编号1…N),第i项活动能够产生a[i]的活跃值。
班级一共有M名学生(编号1…M),邀请编号为i的同学来参加班级建设活动需要消耗b[i]的活跃值。
每项活动都需要某些学生在场才能够进行,若其中有任意一个学生没有被邀请,这项活动就没有办法进行。
班级建设的活跃值是活动产生的总活跃值减去邀请学生所花费的活跃值。
小Hi和小Ho需要选择进行哪些活动,来保证班级建设的活跃值尽可能大。
比如有3项活动,4名学生:
第1项活动产生5的活跃值,需要编号为1、2的学生才能进行;
第2项活动产生10的活跃值,需要编号为3、4的学生才能进行;
第3项活动产生8的活跃值,需要编号为2、3、4的学生才能进行。
编号为1到4的学生需要消耗的活跃值分别为6、3、5、4。
假设举办活动集合为{1},需要邀请的学生集合为{1,2},则得到的班级活跃值为5-9 = -4。
假设举办活动集合为{2},需要邀请的学生集合为{3,4},则得到的班级活跃值为10-9 = 1。
假设举办活动集合为{2,3},需要邀请的学生集合为{2,3,4},则得到的班级活跃值为18-12 = 6。
假设举办活动集合为{1,2,3},需要邀请的学生集合为{1,2,3,4},则得到的班级活跃值为23-18 = 5。
小Hi和小Ho总是希望班级活跃值越大越好,因此在这个例子中,他们会选择举行活动2和活动3。
对于我们题目中的例子来说,其转化的网络流图为:
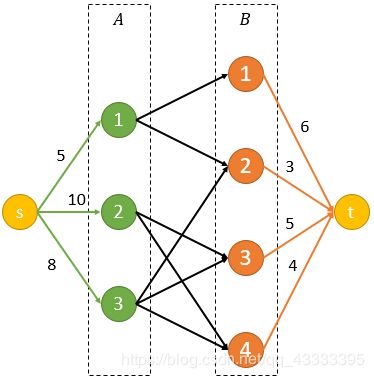
上图中黑边表示容量无穷大的边。
求最大流即最小割。
最大权闭合图:最大权值=正点权之和-最小割
(具体详情请看 博客)