leetcode【每日一题】236. 二叉树的最近公共祖先 Java

我的leetcode代码都已经上传到我的git仓库https://github.com/ragezor/leetcode

题干

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

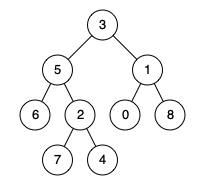
例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。

想法

这道题有两种方法，分别是递归和实现父指针。

递归

树的规律性问题自然想到递归没什么好说的。
假设我们实现了这个函数好吧，如果我们实现了它。
那么我可以对左右子树分别调用这个函数，使得找到现在对应的p，q的最近公共祖先节点。
然后如果p，q都非空，就意味着确实找到了。并且因为左右子树的最近公共祖先，肯定就是这个树呀。
那么返回root即可，相反如果返回值左为空，那么证明两个都在右边，那么返回右子树。
返回值右为空同理。
代码对应后边的lowestCommonAncestor函数

父指针

因为题干上说了所有节点的值都是唯一的。
那么给定一个节点值，我们就可以一对一找到父亲节点。
那么先dfs，把每个节点对应的父亲节点放入map。

然后再从p向上找，每遍历到一个父亲节点，那么就把这个节点放入set里。
如果q已经存在于这个set，证明q是p的最近祖先节点，返回即可
然后再q往上找。
都没找到，ok 返回null
代码对应后边的lowestCommonAncestor2函数

Java代码

package daily;

import java.util.HashMap;
import java.util.HashSet;
import  java.util.Set;

public class LowestCommonAncestor {
    //map存对应的父节点
    HashMap<Integer,TreeNode> map=new HashMap<>();
    //set存访问过的节点
    Set<Integer> visited=new HashSet<>();


    public static class TreeNode {
      int val;
      TreeNode left;
      TreeNode right;
      TreeNode(int x) { val = x; }
 }
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        //空处理
        if(root==null){
            return null;
        }
        //root就是目标
        if(root==p||root==q){
            return  root;
        }
        //左右递归
        TreeNode left=lowestCommonAncestor(root.left,p,q);
        TreeNode right= lowestCommonAncestor(root.right,p,q);
        //左空返回右子树
        if(left==null){
            return  right;
        }
        //右空返回左子树
        else if(right==null){
            return  left;
        }
        //两边都有就是找到了
        else {
            return  root;
        }

    }

    public TreeNode lowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) {
        dfs(root);
        //往上找，把p的放进去
        while(p!=null){
            visited.add(p.val);
            p=map.get(p.val);
        }
        //q的值在p的父亲里
        while (q!=null){
            if(visited.contains(q.val)){
                return  q;
            }
            q=map.get(q.val);
        }
        return  null;

    }

    //dfs 把父节点对应搞定
    public void  dfs(TreeNode root){
        if(root.left!=null){
            map.put(root.left.val,root);
            dfs(root.left);
        }
        if(root.right!=null){
            map.put(root.right.val,root);
            dfs(root.right);
        }

    }

        public   static  void main(String[] args){
        TreeNode node=new TreeNode(3);
        node.left=new TreeNode(5);
        node.left.left=new TreeNode(6);
        node.left.right=new TreeNode(2);
        node.left.right.left=new TreeNode(7);
        node.left.right.right=new TreeNode(4);
        node.right=new TreeNode(1);
        node.right.left=new TreeNode(0);
        node.right.right=new TreeNode(8);

        LowestCommonAncestor lowestCommonAncestor=new LowestCommonAncestor();
            TreeNode res=lowestCommonAncestor.lowestCommonAncestor(node,node.left,node.left.right.right);
            TreeNode res2=lowestCommonAncestor.lowestCommonAncestor2(node,node.left,node.left.right.right);

            System.out.println(res==null? null:res.val);
            assert res != null;
            System.out.println(res2==null? null:res.val);

        }

}

我的leetcode代码都已经上传到我的git仓库https://github.com/ragezor/leetcode