快速排序以及优化（单路排序、二路排序以及三路排序）

快速排序

快速排序算法，我们习惯称为“快排”。现在，我们先来看看快排的核心思想。

快排思想：

选取待排序数组的任意一个数据作为基准值，遍历数组中的元素。将小于基准值的元素放在基准值的左边，大于基准值的放在基准值的右边，将基准值放在中间，此时基准值到达了最终位置。然后对基准值左边的子数组和右边的子数组采用同样的方式进行处理，直到区间缩小为1，就说明数组有序。

单路快排：

快排递归的实现：

private static void quickSortInternal(int[] array,int p,int r) {
if (p >= r) {
return;
  }
//获取分区点
int q = partition(array,p,r);
quickSortInternal(array,p,q-1);
quickSortInternal(array,q+1,r);
}

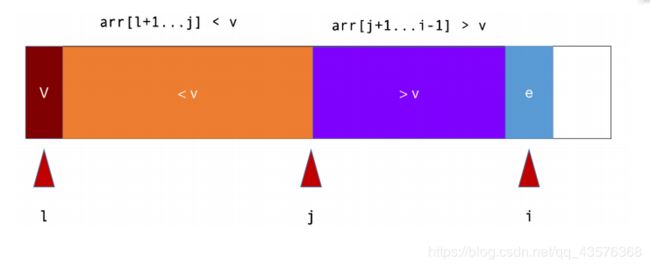
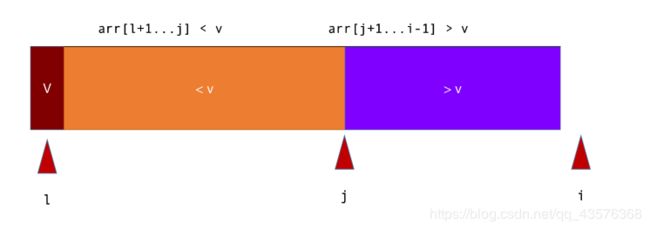
如上图所示，每次我们选取待排序元素的第一个作为基准值，从第二个元素开始向后遍历，i只想当前正在遍历的元素，[l+1,j]区间的元素小于V，[j+1,i-1]区间的元素大于V。每当碰到比分区元素小的节点就与array[j+1]节点进行交换，橙色区域就扩大一个长度，如下图：

最后只需要将下标为l和j的元素进行交换即可。

原地分区代码实现：

private static int partition(int[] array,int l,int r) {

	//默认基准值为第一个元素
    	int v = array[l];
    	int j = l;
		for (int i = l + 1;i <= r;i++) {
	     //比基准值小的元素与j+1位置进行交换，小于区间+1
			if (array[i] < v) {
				swap(array,j+1,i);
				j++;
	 	}
 	}
	swap(array,l,j);
	return j; 
}
/**
* 交换数组中两个索引下标的元素
*/
	private static void swap(int[] array,int x,int y) {
		int temp = array[x];
		array[x] = array[y];
		array[y] = temp; 
}

上述代码缺点：

• 当待排序的集合近乎有序时,由于默认选择的第一个元素作为基准值,会导致基准值划分的两个子数组严重不平衡,此时分层下来的结果近乎于n层,此时快排退化为复杂度为O(n^2)的排序算法

• 解决:随机选取一个元素作为基准值,来降低每次都选到最小或最大值的概率

优化的代码块：

// 随机选取待排序数组中的任意一个元素
int randomIndex = (int) (Math.random()*(r-l+1) + l);
swap(array,l,randomIndex);
int v = array[l];

双路快排
单路快排中只考虑到了大于小于的情况，而等于却没有考虑。这样会出现什么问题呢？当待排序集合包含大量重复元素时,由于与基准值相等的元素个数过多,导致数组长度不均衡,此时分层下来的结果近乎n层,快排退化为O(n^2)

优化：二路快排

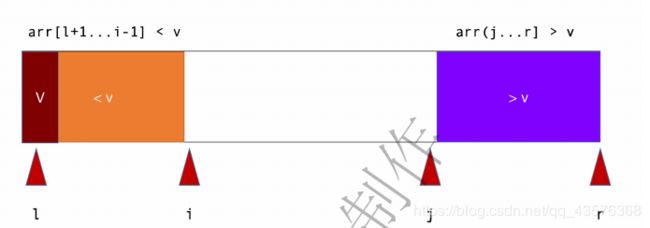
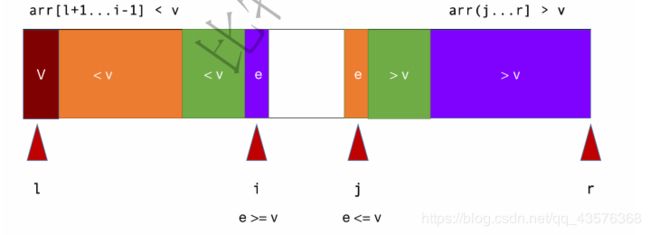
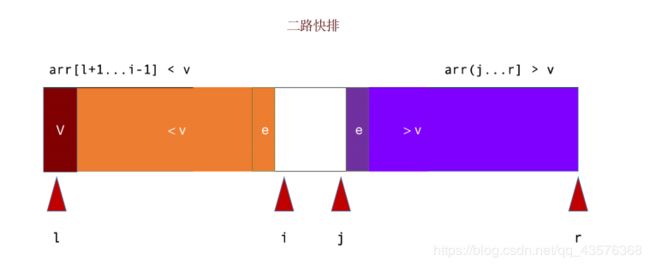
将大于和小于v的元素放在数组的两端，引用新的索引j记录大于V的边界位置。

i索引不断向后扫描,当i的元素小于v时,i++;j索引不断向前扫描,当j的元素大于v时,j- - ;

当i碰到一个>= v的元素以及j碰到一个小于等于 v的元素,交换i与j的元素,i++,j–

双路快排代码实现：

private static int partition2(int[] array,int l,int r) {
	int randomIndex = (int) (Math.random()*(r-l+1) + l);
	swap(array,l,randomIndex);
	int v = array[l];
	int i = l+1,j = r;
	while (true) {
		while (i <= r && array[i] < v) i++;
		while (j >= l+1 && array[j] > v) j--;
		if (i > j) {
			break;
 		 }
		swap(array,i,j);
		i++;
		 j--;
  }
	swap(array,l,j);
	return j; 
}

三路快排：
将整个数组按照划分值v，分成小于v的区域称为小于区，等于v的区域等于区和大于v的区域大于区三部分，在下一次的递归中就不必再处理等于v的等于区，因为等于区的元素已经到达了最终位置，对于存在大量等于v的数组三路快排大大提升了效率。

代码实现如下：

private static void quickSortInternal3(int[] arr,int l,int r）{
	if (l >= r) {
	return;
  }
	int randomIndex = (int）(Math.random()*(r-l+1) + l);
	swap(arr,l,randomIndex);
	int v = arr[l];
	// arr[l+1...lt] < v
	int lt = l;
	// arr[lt+1...i-1] == v
	int i = l + 1;
	 // arr[gt...r] > v
	int gt = r + 1;
	while (i < gt) {
		if (arr[i] < v) {
			swap(arr,i,lt+1);
			lt++; 
			i++;
  }else if (arr[i] > v) {
			swap(arr,i,gt-1);
			gt--;
  }else {
			i++;
  }
  }
	// 循环走完只需要将l位置与lt交换即为分区点
	swap(arr,l,lt);
	quickSortInternal3(arr,l,lt-1);
	quickSortInternal3(arr,gt,r);
}

算法分析：

• 时间复杂度： 最好O（nlogn），最坏O（n*n）。

• 空间复杂度
  递归调用本质在不断压栈，因此快排的空间复杂度与递归的深度有关，
  最好的情况是 O（logn），最坏O（n）。

• 稳定性：不稳定