计算机组成原理——计算机运算部分

1.概述

存储容量与地址总线之间的关系

1kb=2¹⁰b 需要10根地址总线
1Mb=2¹⁰kb = 2¹⁰*2¹⁰b =2²⁰b需要20根地址总线
1GB=2¹⁰Mb=2¹⁰*2¹⁰*2¹⁰b=2³⁰b 需要30根地址总线
2GB=2 *2³⁰b=2³¹b需要31根地址总线

计算机系统性能评价

1.非时间指标：

• 机器字长：指机器一次能处理的二进制位数。
• 总线宽度：数据总线一次能并行传送的最大信息位数。（有时外总线与内总线数量并不一致）
• 主存容量与存储带宽。

2.时间指标

• 主频f:cpu内核工作时钟频率，即cpu数字脉冲信号振荡速率，与cpu实际运算能力之间不是唯一直接的关系。主频=外频*倍频
• 时钟周期：一个时钟周期内，cpu仅完成一个最基本的动作。
• 外频：指cpu（内存）与主板之间同步的时钟频率。
• 倍频：cpu主频与外频之间的倍数。
• CPI：执行一条指令（平均）需要的时钟周期数。（单条指令CPI，指令系统CPI等）CPI=程序中所有指令的时钟周期数之和/指令中指令总数=∑（程序中各类指令的CPI*程序中该类指令的比例。{IPC指每个时钟周期内执行的指令条数（并行）}
• MIPS:每秒钟执行的指令条数，以每秒百万条指令做单位。 MIPS=执令条数/(执行时间*10⁶) MIPS=f/(CPI*10^6){全性能公式}
• cpu时间：执行一段程序所需时间（CPU时间+I/O时间+存储访问时间+各类排队延时等）cpu时间=程序中所有指令的时钟周期数之和=总指令数*CPI *T
  cpu时间=程序的执行时间t=指令数量/（MIPS * 10⁶）

2.机器数及特点

机器内数据的表示

1. 真值：符号用“+”、“-”表示的数据表示方法。
2. 机器数：符号数值化的数据表示方法，用0、1表示符号。
3. 三种常见的机器数：原码、反码、补码表示。设定点数的形式为X₀X₁X₂…X _n
   （注意：[+0]_原=00000，[-0]_原=10000，[+0]_反=00000，[-0]_反=11111），[+0]_补=00000=[-0]_补=00000)

常见机器数的特点

一、真值：将带符号位的机器数对应的真正数值称为机器数的真值，例如0000 0001的真值=+000 0001=+1
二、原码(数值前加一位符号位)
1.表示简单：[x]_原=2ⁿ-1
2.运算复杂：符号位不参加运算，要设置加法、减法器。
3.0的表示不唯一（不能直接判定是执行加法还是减法运算，分同号和异号)
三、反码：（正数的反码与原码相同，负数的反码除符号位，其余按位取反）
1.表示相对复杂：[x]_反=2ⁿ⁺¹+X-1
2.运算相对原码简单：符号位参加运算，只需要设置加法器，但符号位的进位位需要加到最低位。
3. 0的表示不唯一
四、补码：正数的补码与原码相同，负数的补码等于反码+1，在计算机中用补码表示负数。
1.表示相对原码复杂：[x]_补=2ⁿ⁺¹+X
2.运算简单：只需设置加法器
4. 0的表示唯一
补码中模的概念（符号位进位后所在位的权值）
五、移码（增码）：补码的数值部分不变，符号取反。[x]_移=2ⁿ+X，X为真值，n为X的整数位位数。
移码表示浮点数的阶码，在移码表示表示中“1”表示正数的符号，“0”表示负数的符号。与前面有所不同

3.定点与浮点数的表示

定点数据表示

1.可表示定点小数和整数
2.表示形式：X₀X₁X₂…X_n（小数点在中间某位上是定点小数，小数点在最后为定点整数）
3.定点小数表示数的范围（补码为例）：-1<=X<=1-2^-n
4.定点整数表示数的范围（补码为例）：-2ⁿ<=X<=2ⁿ-1
5.定点数据表示数的不足：数据表示范围受限

浮点数据表示

**把数的范围和精度分别表示的一种数据表示方法。**当数的表示范围超出了定点表示的范围时使用浮点数据表示。
1.格式（一般格式：数据移植性太差）
E_s E₁ E₂…E_n M_s M₁M₂…M_k——> N=2^e.m
E:阶码位数，决定数据的范围
M:尾数位数，决定数的精度（位数固定，若想表示较大的数据则只能牺牲精确度）
2.IEEE 754格式

S(符号位)	8位偏指数E	23位有效尾数M	单精度
S(符号位)	11位偏指数E	52位有效指数M	双精度

• 指数采用偏移值（对阶码进行移位变为移码）其中单精度偏移值为127，双精度为1023。将浮点数的阶码值变成非负整数，便于浮点数的比较和排序。
• IEEE754尾数形式为1.XXXXXX，其中M部分保存的是XXXXXX（1被隐藏），从而可保留更多的有效位，提高数据表示的精确度。
• 将上述IEEE754格式对应的32位浮点数还原为真值时：
• N=（-1）^s * 2^E-127 * 1.M,随E、M的取值不同，IEEE754浮点数据表示具有不同的意义。
  
  IEEE754 32位浮点数与对应真值之间的变换流程如下
  
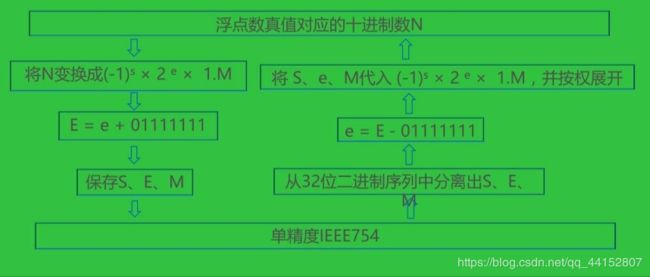
  其上0111 1111是127对应的二进制数

e.g  将十进制数20.59375=10100.10011*2^4转换成32位IEEE754格式
的浮点数的二进制格式。
解：先将十进制数换成二进制数：
20.59375=10100.10011
移动小数点，使其变成1.M的形式
10100.10011=1.010010011*2^4
得到：S=0，e=4（十进制格式变便二进制相加），
E=100+0111 1111=1000 0011,
M=0100 10011
最后得到32位浮点数的二进制存储格式为：
0100 0001 1010 0100 1100 0000 0000 0000
=41A4C000H（16进制）

4.数据校验

校验的基本原理

1.增加冗余码（校验位）

有效信息位（k位）	校验信息位（r位）

码距的概念

• 同一编码中，任意两个合法编码之间不同二进制位数的最小值；
• 0011与0001的码距为1，一位错误时无法识别；
• 校验码中增加冗余码的目的时为了增大码距。
• 码距>=e+1可以检测e个错误
• 码距>=2t+1可以纠正t个错误
• 码距>=e+t+1可以纠正t个错误，同时检测e个错误（e>=t)
• 码距越大，抗干扰强，纠错能力强，数据冗余越大，编码效率越低，编码电路也相对复杂；
• 选择码距必须考虑信息发生差错的概率和系统能容许的最小差错率。

奇偶校验

1.增加冗余码（校验位）
2.编码：根据有效信息计算校验信息位，使校验码（数据+1位校验信息）中1的个数满足奇偶校验的要求。偶校验：即1的个数为偶数个。奇校验即1的个数为奇数个。

奇偶校验的特点

• 编码与检错简单
• 编码效率高
• 不能检测偶数位错误，无错结论不可靠，是一种错误检测码。
• 不能定位错误，因此不具备纠错能力。
• 奇偶校验的码距是2.

改进奇偶校验

• 双向奇偶校验（横向和纵向都校验）
• 方块校验
• 垂直水平校验
  1.可以纠正一位错误，2.可以检测出某行（列）上的奇数位，3.可检测一部分偶数位错误。4.不能检测出错码分布在矩形4个顶点上的错误。

奇偶校验的应用

1.判断内存条是否支持奇偶校验（9位才可）
2.工程上，关于串口奇偶校验配置
3.一般在同步传输方式中采用奇校验，异步传输采用偶校验

CRC（循环冗余校验）校验

CRC校验的基本原理

• 增加冗余码（校验位）

有效信息位（k位）	校验信息位（r位）

N=k+r<=2^r-1

• 生成多项式G（x）

收发双方约定一个（r+1）位二进制数，发送方利用G（x）对信息多项式做模二除运算，生成校验码。接收方利用G（X）对收到的编码多项式做模二除运算检测差错及错误定位。

• G（X）应该满足的条件
  1.最高位和最低位必须为1
  2.当被传送信息（CRC码）任何一位发生错误时，被生成多项式做除后应该使余数不为0；
  3.不同位发生错误时，模二除运算后余数不同
  4.对不为0余数继续进行模二除运算应使余数循环。

---

通俗说：双方约定个r位的除数(生成项)，在被除数(信息位)后面补r-1个0。此时的除数与被除数做模二运算(加减法部分进行异或的除法运算)后得到的余数(校验码)补在原始被除数的后面得到数m，将数m与生成项发给接收方。这时接收方将数m与生成项相除余数为0，则表示接收正确。 最终得到的余数个数与补的位数要相同

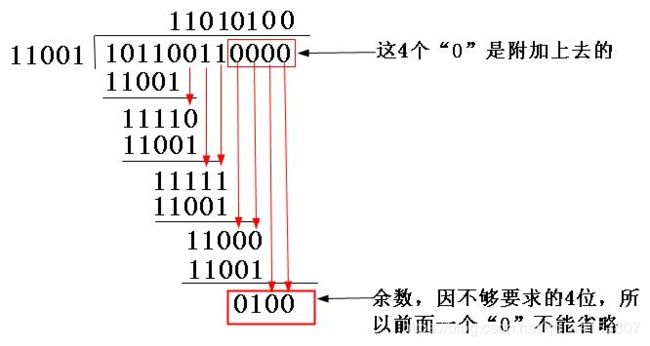
生成多项式:G(X)=X4+X3+1，要求出二进制序列10110011的CRC校验码。
（1）G(X)=X4+X3+1,二进制比特串为11001;(有X的几次方，对应的2的几次方的位就是1)
（2）因为校验码4位，所以10110011后面再加4个0，得到101100110000，用“模2除法”(其实就是亦或^)即可得出结果；

（3）CRC^101100110000得到101100110100。发送到接收端；
（4）接收端收到101100110100后除以11001(以“模2除法”方式去除),余数为0则无差错；

部分转载参考https://www.cnblogs.com/bugutian/p/6221783.html
移位法计算余数
 先取出与生成项(除数)位数相同的(r位)被除数前一部分与生成项异或，得到的数首位是1则异或，首位是0则左移直到遇到1，左移造成的右端空缺补0。依次类推直到取出的这一部分全部运算完后所得到的余数再与被除数后一部分再异或得到的数就是最终余数。

(除数)除(被除数)得商——>3除6=2
(被除数)除以(除数)得商——>6除以3=2
(被除数)被(除数)除得商——>6被3除等于2
以上6是被除数，3是除数，2是商
0不能做除数——>不能除以0——>不能被0除

参考与部分转载：https://blog.csdn.net/BeautifulPebbles/article/details/86751411

---

模2运算

• 加减运算（异或运算，加不进位，减不借位）
• 异或：相同得0，相异得1
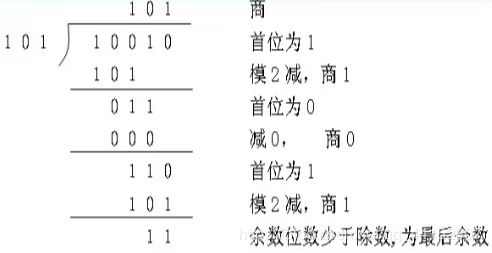
• 模2除法：按模2减，求部分余数，不借位。
• 上商原则:[1].部分余数首位为1时，商为1，减除数；[2].部分余数首位为0时，商为0,减0.[3].当部分余数的位数小于除数的位数时，该余数即为最后余数。
  

CRC编码方法

1.根据待校验信息的长度k，按照k+r<=2^r-1确定校验位r的位数，如对四位信息1100进行RCR编码，根据4+r<=2^r-1得r_min=3.
2.根据r和生成多项式的选择原则，选择位数为r+1的生成多项式G（X）=1011（查表）
3.进行下列变换

有效信息位（k位）	校验信息位（r位）
1100	000

即：将待校验的二进制信息Q（X）逻辑左移r位，得到Q（X）‘
4.对Q（X）‘按模2运算法则除G（X），求CRC编码中的r位校验信息。
用得到的余数替换Q（X）‘的最后r位即可得到最后的CRC编码
1100|000——>1100|010 即为1100的CRC编码
接收方利用G（X）对收到的编码多项式做模2除运算

CRC的校验与纠错

余数为0，说明传输没有错误。错误在不同位数对应的余数不同。
若采用不同的生成多项式，对应的相同位出错的时候得到的不为0的余数是不相同的。

• 利用出错情况下余数循环特性进行纠错
• 若余数不为0，一边对余数补0做模二除，同时让被检测的校验码循环左移，当余数为101时，出错位也移到A1位置。通过异运算纠正后继续循环左移和执行余数模二除法，直到修改后的出错位回原位。不需对每一位提供纠正电路。
• 当位数增多时，循环校验码能有效的降低硬件代价，这是它得以广泛应用的主要原因。
• 可硬件实现通过异或
• 也可以软件实现（通过代码）

海明校验及其实现

1.增加冗余码（校验位）

有效信息位（k位）	校验信息位（r位）

N=k+r<=2^r-1
设K+r位海明码从左至右依次为第1，2，3…，k+r位，r位校验位记为P_i（i=1，2，…,r）,分别位于k+r位海明码的第2^i-1(i=1,2,…r)位上，其余位依次放置被校验位的数据位。
eg.被校验的信息是7位即（7，4）海明校验中校验位和被校验信息位的排列如下：

海明码位号Hj	1	2	3	4	5	6	7	8	9	10	11
P和b的分布	P1	P2	b1	P3	b2	b3	b4	P4	b5	b6	b7

由公式得校验位分别位于海明码的第1，2，8位上
海明校验用到的是奇偶校验的方法
在海明编码H_j位上的数据被编号小于j的若干个海明位号之和等于j的校验位所校验

海明码位号Hj	1	2	3	4	5	6	7	8	9	10	11
P和b的分布	1	2	1,2	4	1,4	2,4	1,2,4	8	1,8	2,8	1,2,8
	/p1	/p2	/b3	/p3	/b2	/b3	/b4	/p4	/b5	/b6	/b7

比如海明位号为7=1+2+4，而1，2，4是校验位，则7上的b4可由1，2，4位上的P1、P2、P3校验。b4=P1+P2+P3
由此可采用偶校验计算出P₁-P₄四个校验位的值
P1=b1⊕b2⊕b4⊕b5⊕b7
P2=b1⊕b3⊕b4⊕b6⊕b7
P3=b2⊕b3⊕b4
P4=b5⊕b6⊕b7
4.设置指错字G₄G₃G₂G₁
G₄=P4⊕b5⊕b6⊕b7（将上式中P4与b5之间的等号变为异或）
G₃=P3⊕b2⊕b3⊕b4
G₂=P2⊕b1⊕b3⊕b4⊕b6⊕b7
G₁=P1⊕b1⊕b2⊕b4⊕b5⊕b7
可以指出是否发生错误，并定位错误。
G₄G₃G₂G₁为0则表明无错误，反之对应位指出出错位的海明码位号。据所得到的二进制值转位十进制即海明位相应出错的位置。配合适当额电路和异或门，修正出错位。
海明校验的特点：

• 指错字G₄G₃G₂G₁=0000不一定无错，如P1、b1、P2三位同时出错，则G2、G1仍然为0.
• 一位错和两位错不能由指错字区别。比如b1、b2同时出错，与仅b3出错时的指错字均为G₄G₃G₂G₁=0110
• 可以在海明校验的基础上增加一位奇偶校验位判断是一位错还是两位错。

5.定点数运算及溢出检测

补码

补码：补码的意义是负数可以用正数来代替。

• 如在四位二进制条件下-1011=+0101（mod 2⁴）即-11变成了+5.
• mod 2代表按2取模，-5在模12的情况下补是+7.纯小数的mod取2，纯整数的mod取2ⁿ⁺¹
• mod 2ⁿ⁺¹是取二进制的第一位（2⁰）位到第n+1位（2ⁿ）位，而忽略更高位。
• 两个八位数字相加若得到一个九位的数字，则最高位会溢出舍去即舍去最左边的一位。

定点数加法运算

[X]_补+[Y]_补=[X+Y]_补mod 2ⁿ⁺¹其中n是字长即有效数据的位数。

• 不需要事先判断符号，符号位与码值位一起参与运算，符号位相加后若有进位，则舍去该进位数字，因在模2^n+1^的意义下相加，即大于2^n+1^的进位要丢掉。
• 当求两个二进制的加法时，先转换位对应的补码再利用上述相加，不要直接相加。得到的数为机器数，要得到最终的真值则要再求补为最终真值。即除符号位逐位取反再加1.

定点数的减法运算

[X-Y]_补=[X]_补-[Y]_补=[X]_补+[-Y]_补
根据Y的补码求-Y的补码：根据Y的补码求出Y的值，再得到-Y的值，据-Y的值求出-Y的补码。

• 简便方式：通过从右向左扫描[X]_补，在遇到数字1及之前，直接输出遇到的数字，遇到1之后，取反输出，即可得到[-Y]_补，反之亦然。
• [-B]_补的求法是[B]_补连同符号位在内，每位取反，末尾加一。
• 知补码求源码：若补码符号位为0，表示是一个正数，补码就是源码；符号为为1，表示负数，除符号位逐位取反再加1.

数溢出的概念及其判断方法

1） 溢出的概念
运算结果超出了某种数据类型的表示范围。
2）溢出的检测方法

• 溢出只可能发生在同符号数相加时，包括[X]_补与[Y]_补；对于减运算而言：[X]_补+[-Y]_补同号。

（1）方法一：对操作数和运算结果的符号位进行检测。

• 当操作数的符号位与操作数的符号位不相同时就表明发生了溢出。
• 比如：两个正数相加结果是负数。
• （设X0，Y0为参加运算数的符号位，S0为结果的符号位)，有V=X₀Y₀！S₀+！X₀！Y₀S₀，其中（！X₀表示X₀的非）
• 当V=1时，运算结果溢出，根据该逻辑表达式，容易画出相应的电路图。
  （2）方法二：对最高数据位进位和符号位进行检测
• 设运算时最高数据位产生的进位为C₁，符号位产生的进位为C₀
• 溢出检测电路为：V=C₀⊕C₁，这两个不同步时溢出。

（3）方法三：用变型补码

• [X]_补=X_f1X_f2.X₁X₂X₃…X_n mod 2ⁿ⁺²(双符号位) 。（如负数的符号位上是11）
• 模是最高符号位进位位所在的权值。
• 溢出判断：V=X_f1⊕X_f2,只要两个符号位不同，则其发生溢出了。
• 用双符号方式进行运算，运算结果符号位不一致则溢出

（4）可通过代码判断，影响流水线效率。

无符号位的溢出判断

• 无符号数加法的溢出可用ALU表示
• 无符号数减法的溢出也可用带加/减功能的ALU的进位取反后表示。为1表示没有溢出，为0表示有溢出。

6.一位乘法

原码一位乘法

移位操作及其意义

逻辑左移：数据逻辑整体左移后，右边空出来的低位补0
算数左移：方法与逻辑左移一致，但是意义不同。算数左移相当于乘2.
逻辑右移：数据整体向右移一位，最高位补0，最低位被移出。
算数右移：数据整体右移一位，最高位被原来最高位复制填补，最低位被移出，相当于除2.

由此可见
a.乘法可由加法实现，若要用加法器实现乘法需要解决几个问题1.需要多输入的全加器（最多为n+1）：采用循环累加0或乘数的方式；2.需要长度为2n的积寄存器：从部分积和乘数寄存器取结果。3.对应乘数的不同位，部分积左移次数不同，且乘法过程中总移位次数多。：右移部分积，放到乘数寄存器中，此处右移的位不能丢掉；

原码一位乘法

• 符号位单独参加运算，数据位取绝对值参加运算。

• 运算规则：先求X，Y的原码，结果的符号位由两个原码的符号位异或运算得到，数据位取绝对值相乘运算。
  设：[X]_原=X₀.X₁X₂…X_n
  [Y]_原=Y₀.Y₁Y₂…Y_n
  则：符号位P0=X₀⊕Y₀
  数据位|P|=|X|.|Y|

• 运算过程采用改进的乘法运算方法。
  下文是一位大神关于原码一位乘法清爽简单的解释：
  ————————————————————————————
  x * y = z
  讨论已知x和y的情况下，怎么通过原码一位乘法方法得出z~~
  首先说下运算规则~
  1. z的符号位通过x和y的符号位进行异或运算得到_{（这个很好理解哒，负负得正，正正得正，正负得负嘛}所以把符号位异或得到的结果就是乘法运算后应该的结果咯~）
  2. 所以就不用讨论x和y的符号位啦，z除了符号之外的其他部分由x的绝对值乘以y的绝对值得到~
  1、2两点总结一下就是说：被乘数和乘数均取绝对值参加运算，符号位单独考虑~
  我们手工进行乘法运算的时候，是通过y从右往左每一位都和x相乘，（乘完一次就往前缩进一个数位）然后把结果相加得到的_{机器也是这样运算哒}不过机器为了节约空间，毕竟按照手算的方法那样两个n位相乘最后可能会需要2n的长度空间才能得到结果，计算机是采用把每次用y的一位和x相乘的结果（叫做部分积）累加后右移一位，再处理y当前位的下一位的~
  3. 我们把被乘数x先取双符号，而且让部分积初始值为0，并且长度和被乘数x相同（就是添0让长度相同的意思啦~）
  计算机只有0和1，所以处理乘法的时候运算法则远没有99乘法表那么复杂，运算规则为：
  4. 从y的最后一位开始（一直到第一位）分别与x相乘：
  当y的当前位为1，则部分积加上x的绝对值
  当y的当前位为0，则部分积加上0
  5. 右移一位，在前面加0。不断处理y的每一位，知道y的所有位都处理过为止~
  可能有点晕，举个栗子~
  比如x = 0.1101 ，y = 0.1011
  先把部分积设为初始值0（长度扩展到和x相同），即
  00.0000
  y的最后一位是1，所以要加上x的绝对值：
  00.0000 + 00.1101 = 00.1101
  右移1位，前面补0，变成了00.01101

  好啦，下面处理y的倒数第二位，还是1，继续加x的绝对值：
  00.01101 + 00.1101 = 01.00111
  别忘记右移1位，前面补0，这样就变成了00.100111

  y倒数第3位是0，只要加0就好了（加0的结果还是本身啊。），所以还是：00.100111
  既然加了0，别忘记右移一位哦，所以变成了00.0100111

  y还剩最后一个位（也就是第一位）没处理啦，第一位是1哦，那就加上x的绝对值：
  00.0100111 + 00.1101 = 01.0001111
  别忘记右移一位！所以最后结果是 00.10001111~
  嗯好啦，这就是最后结果，不过双符号位就变成一个0就好咯，也就是最后结果为0.10001111。
  ———————————————————————————
  版权声明：本部分文为CSDN博主「柳婼」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
  大神解释原文链接
  ——————————————————————————————

补码一位乘法（Booth）

[X]_补=X₀.X₁X₂…X_n
[Y]_补=Y₀.Y₁Y₂…Y_n
[x*y]_补=[X]_补*∑(y_i+1-y_i)2^-i(符号位参加运算)
如果y_n+1=y_n’部分积加0，部分积算数右移一位；
如果y_n+1y_n=10,部分积加[x]_补,部分积算数右移一位。
重复进行n+1步，但最后一步不移位。
包括一位符号位，所得乘积为2n+1位，其中n为数据位位数。

下文是一位大神关于原码一位乘法清爽简单的解释：
————————————————————————————
x * y = z
讨论已知x和y的情况下，怎么通过补码一位乘法方法得出z～
首先说下运算规则～
和原码一位乘法不同的是，补码一位乘法的符号位是参加运算的~运算的所有的数包括得到的结果z都是补码的形式～
被乘数x取双符号参与运算，部分积的初值为0~~乘数y取单符号位～
乘数y末尾首先要增加一个附加位0，每次讨论的是y的最后两位~但是每次移动是移动一位哦～
**判断y的最后两位的时候，遵循这样的规则：
为00或者为11的时候，直接右移一位
为01的时候，加x的补，然后右移一位
为10的时候，加-x的补，然后右移一位

5. 不过有个特例，就是最后一步不用右移一位！**

举个栗子～

比如x = -0.1101，y=0.1011

先写出x的补码：[x]补 = 11.0011，再写出-x的补码：[-x]补 = 00.1101

一开始部分积的初值是：00.0000

在y后面加个0~那么y变成了0.10110
然后从y的最后两位开始往前，0.10110当前最后两位是10，所以加上[-x]补：
00.0000 + 00.1101 = 00.1101
右移一位，变成00.01101

此时y =0.10110的最后两位变成了11（是往前挪了一个位置哦，不是两个~），按照规则应该直接右移一位就好啦，就变成了00.001101

此时y =0.10110的最后两位变成了01，所以根据规则要加[x]补：

00.001101 + 11.0011 = 11.011001

右移一位，变成了11.1011001

此时y =0.10110的最后两位变成了10，加上[-x]补：

11.1011001 + 00.1101 = 00.1000001

右移一位，变成了：00.01000001

此时y =0.10110最后两位是01（所以从这里就可以知道规则里面要在y前面补一个0的作用了吧嘿嘿），加[x]补：

00.01000001 + 11.0011 = 11.01110001

因为这已经是最后一步了，所以不用再右移了，所以最后结果就是1.01110001

这个结果是x*y的补码哦～
——————————————————————————————————
版权声明：本文为CSDN博主「柳婼」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
大神解释原文链接

7.总线结构

判优控制

• 主设备（模块） 对总线有控制权
• 从设备（模块） 响应从主设备发来的总线指令
  $总线判优控制\{\begin{array}{ll}集中式& \{\begin{array}{l}链式查询\\ 计数器定时查询\\ 独立请求方式\end{array}\\ 分布式& \end{array}$​

链式查询方式

主线通信控制

为了解决通信双方协调配合问题
总线的传输周期
$总线的传输周期\{\begin{array}{ll}申请分配阶段& 主模块申请，主线仲裁决定\\ 寻址阶段& 主模块向从模块给出地址和命令\\ 传数阶段& 主模块和从模块给出地址和命令\\ 结束阶段& 主模块撤销有关信息\end{array}$​

总线通信的四种方式

$总线通信的四种方式\{\begin{array}{ll}同步通信& 由统一时标控制数据传送\\ 异步通信& 采用应答方式，没有公共时钟标准\\ 半同步通信& 同步、异步结合\\ 分离式通信& 充分挖掘系统总线每个瞬间的潜力\end{array}$

半同步通信（同步、异步结合）

同步 发送方用系统时钟前沿发信号
   接收方用系统时钟后沿判断、识别
异步 允许不同速度的模块和谐工作
   增加一条”等待响应信号“
一个总线传输周期（以输入数据为例）

• 主模块发地址、命令     占用总线
• 从模块准备数据       不占用总线，总线空闲
• 从模块向主模块发数据    占用总线

分离式通信

充分挖掘系统总线每个瞬间的潜力
$一个总线传输周期\{\begin{array}{ll}子周期1& 主模块申请占用总线，使用完后即放弃总线的使用权\\ 子周期2& 从模块申请占用总线，将各种信息送至总线上\end{array}$

分离式通信特点

• 各模块有权申请占用总线
• 采用同步方式通信，不等对方回答
• 各模块准备数据时，不占用总线
• 总线被占用时，无空闲