个人笔记:数据库——函数依赖
本文仅供参考学习使用,谢谢
范式部分
文章目录
- 函数依赖
- 1.函数依赖
- 2.平凡函数依赖与非平凡函数依赖
- 3.完全函数依赖与部分函数依赖
- 4.传递函数依赖
- 码
函数依赖
1.函数依赖
设R(U)是一个属性集U上的关系模式,X和Y是U的子集。若对于R(U)的任意一个可能的关系r,r中不可能存在两个元组在X上的属性值相等, 而在Y上的属性值不等。则称“X函数确定Y”或“Y函数依赖于X”,记作 X→Y。X称为这个函数依赖的决定属性组,也称为决定因素(Determinant)。
若Y不函数依赖于X, 则记为X ↛ Y。
//例: S(Sno, Sname, Ssex, Sage, Sdept)
F= {Sno→Sname,Sno→Ssex,Sno→Sage,Sno→Sdept} Ssex ↛ Sage, Ssex ↛ Sdept
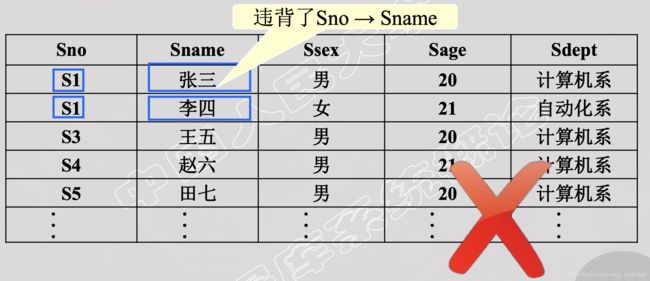
- 函数依赖是语义范畴的概念。只能根据数据的语义来确定函数依赖。
如Sname → Sno函数依赖只有在“学生不允许有重名”的条件下成立。
- 数据库设计者可以对现实世界作强制的规定。
例如设计者可以强行规定不允许学生有重名,因而使函数依赖
Sname →Sno,Sname →Ssex, Sname →Sage,Sname→Sdept 成立。
函数依赖是指 关系模式R在任何时刻的关系实例均要满足的约束条件
不是指某个或某些关系实例 r 满足的约束条件,而是指R的所有关系
实例 r 均要满足的约束条件。
2.平凡函数依赖与非平凡函数依赖
- X→Y,Y⊈X,则称X→Y是非平凡的函数依赖。
- X→Y,但Y⊆X ,则称X→Y是平凡的函数依赖。
//例:在关系SC(Sno, Cno, Grade)中,
非平凡函数依赖:
(Sno, Cno) → Grade
平凡函数依赖:
(Sno, Cno) → Sno
(Sno, Cno) → Cno
对于任一关系模式,平凡函数依赖都是必然成立的,它不反映新的语义,因此若不特别声明, 我们总是讨论非平凡函数依赖。
3.完全函数依赖与部分函数依赖
在关系模式R(U)中,如果X→Y,并且对于X的任何一个真子集X’,都有 X’↛Y, 则称Y完全函数依赖于X,记作X →(F) Y。
若X→Y,但Y不完全函数依赖于X,则称Y部分函数依赖于X,记作X →(P ) Y。
//在关系STUDENT(Sno ,Sdept, Mname,Cno,Grade)中,
F
(Sno, Cno) → Grade 是完全函数依赖
P
(Sno, Cno) → Sdept 是部分函数依赖,因为Sno → Sdept,
4.传递函数依赖
在R(U)中,如果X→Y,(Y⊈X),Y↛X,Y→Z,则称Z对X传递函传递数依赖(transitive functional dependency)。记为:X →(传递) Z。
注意: 如果Y→X, 即X←→Y,则Z直接依赖于X。
//在关系STUDENT(Sno ,Sdept, Mname,Cno,Grade)中
传递
Sno → Sdept,Sdept → Mname,Sno → Mname
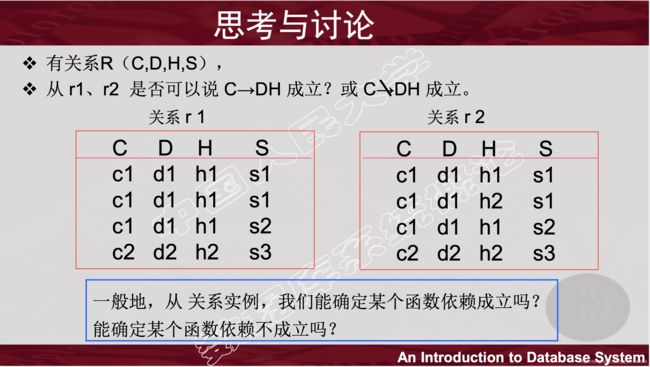
分析:
从定义出发:
设R(U)是一个属性集U上的关系模式,X和Y是U的子集。若对于R(U)的任意一个可能的关系r,r中不可能存在两个元组在X上的属性值相等, 而在Y上的属性值不等
可以得出R1 函数依赖 C -> DH 成立 , R2 的函数依赖 C → DH 不成立
码
设K为关系模式R
- 如果U部分函数依赖于K,即K → U,则K称为超码(Surpkey)
- 候选码是最小的超码,即K的任意一个真子集都不是候选码
//S(Sno, Sdept, Sage)
Sno → (Sno, Sdept,Sage), Sno是码
(Sno, Sdept)、 (Sno, Sage)、 (Sno, Sdept, Sage) 是超码
SC(Sno, Cno, Grade)中,(Sno, Cno)是码
若关系模式R有多个候选码,则选定其中的一个做为主码(Primary key)。
S(Sno, Sname, Sdept, Sage),
假设学生无重名 则 Sno、 Sname是候选码,选择Sno为主码。
主属性与非主属性
- 包含在任何一个候选码中的属性 ,称为主属性(Prime attribute)
- 不包含在任何码中的属性称为非主属性(Nonprime attribute)或非码属性 (Non-key attribute)
S(Sno, Sdept, Sage),Sno是码, Sno是主属性, Sdept, Sage是非主属性。
SC(Sno, Cno, Grade)中,(Sno, Cno)是码,
Sno, Cno是主属性, Grade是非主属性
全码:整个属性组是码,称为全码(All-key)
关系模式 R(P,W,A) P:演奏者 W:作品 A:听众
语义:一个演奏者可以演奏多个作品,某一作品可被多个演奏者演奏,听众可以欣赏不同演奏者的不同作品
R(P,W,A)码为(P,W,A),即全码,All-Key。
——————
关系模式 R
SC(Sno,Cno,Grade)中,Sno不是码,但Sno是关系模式
S(Sno,Sdept,Sage)的码,则Sno是关系模式SC的外部码