重学数据结构之图

一、图

1.基本概念

　　图是一种抽象的数学结构，研究抽象对象之间的一类二元关系及其拓扑性质。而在计算机的数据结构领域中，图则是一种复杂的数据结构。

　　一个图是一个二元组 G = (V, E)，其中：

• V 是非空有穷的顶点集合，也可以有空图。
• E 是顶点偶数对的集合，即两个顶点组成一条边。
• V 中的顶点也被称为图 G 的顶点，E 中的边也被称为图 G 的边。

　　图分为无向图和有向图。在无向图中边没有方向，用圆括号表示，例如(v1, v2)。在有向图中边是有方向的，用尖括号表示，例如。

2.一些概念和性质

1.完全图

　　完全图：任意两个顶点之间都有边的图。完全图有如下性质：

• n 个顶点的无向完全图有 n*(n-1)/2 条边。
• n 个顶点的有向完全图有 n*(n-1) 条边。

2.路径

　　对于图 G=(V, E)，如果存在顶点序列如 Vi₀，Vi₁，...，Vi_n，使得 (Vi₀，Vi₁）、(Vi₁，Vi₂）、...(Vi_n-1，Vi_n）都是图的边，则说从 Vi₀ 到 Vi_n 存在路径，并称 Vi₀，Vi₁，...，Vi_n 是从顶点 Vi₀ 到 Vi_n 的一条路径。对于路径，还有如下概念：

• 路径的长度就是该路径上边的数量。
• 成环的路径就是起点和终点相同的路径。
• 简单路径就是不含环的路径，也就是说除了该路径的起点和终点可能相同外，其他顶点均不相同。

　　需要注意的是，从一个顶点到另一个顶点，可能存在路径，也可能不存在路径。如果存在路径，还可能存在多条路径。

3.连通图

1）连通

　　如果在一个无向图中存在 v_i 到 v_j 的路径，则称这两个顶点连通。

2）连通无向图

　　如果无向图 G 中任意两个顶点之间都连通，则称 G 为连通无向图。

3）强连通有向图

　　如果对于有向图 G 中任意两个顶点 v_i 和 v_j ，从 v_i 到 v_j 连通并从 v_i 到 v_j 也连通，则称 G 为强连通有向图。

4）带权图

　　如果图 G 中的每条边都被赋予一个权值，则称 G 为带权图，可以是有向图也可以是无向图。边的权值可用于表示实际应用中与顶点之间的关联的有关信息，带权的连通无向图也被称为网络。

3.抽象数据类型

　　图作为一种复杂的数据结构，可以给图定义如下操作：

ADT Graph:

　　Graph(self)  # 用于创建一个图

　　is_empty(self)  # 判断图是否为空 

　　get_vertex(self)  # 获取顶点数量

　　get_edge(self)  # 获取边的数量

　　add_edge(self, v1, v2)  # 添加一条 v1 到 v2 的边

　　has_edge(self, v1, v2)  # 是否有 v1 到 v2 的边

　　print(self)  # 打印图

 

二、图的表示和实现

1.邻接矩阵表示法

　　图的最基本表示方法是邻接矩阵表示法。邻接矩阵是表示图中顶点间邻接关系的矩阵，对于一个有 n 个顶点的图 G=(V, E)，其邻接矩阵是一个 n*n 的矩阵，图中每个顶点对应于矩阵里的一行和一列。

　　最简单的邻接矩阵是以0/1为元素的，即对于图 G 的邻接矩阵，当 A_ij 为0时，表示顶点 v_i 和 v_j 无边， 当 A_ij 为1时，表示顶点 v_i 和 v_j 有边。邻接矩阵表示了图中的顶点数量和顶点间的关系（即边），每个顶点对应矩阵的一对行列下标，听过一对下标就可以确定图中的某条边是否存在了。

　　要使用 Python 实现一个图类，可以使用列表（list）或者 numpy 模块里的矩阵（array），这里就用列表来实现，即用 list 为元素的 list，具体代码如下： 

 1 # 使用邻接矩阵
 2 class Graph:
 3     def __init__(self, v):
 4         self.V = v
 5         self.E = 0
 6         self.data = [[0 for _ in range(v)] for _ in range(v)]
 7 
 8     def is_empty(self):
 9         """
10         判断图是否为空
11         :return:
12         """
13         return self.V == 0
14 
15     def get_vertex(self):
16         """
17         获取顶点数量
18         :return:
19         """
20         return self.V
21 
22     def get_edge(self):
23         """
24         获取边的数量
25         :return:
26         """
27         return self.E
28 
29     def add_edge(self, v1, v2):
30         """
31         向图中增加一条v1到v2的边
32         :param v1: 顶点
33         :param v2: 顶点
34         :return:
35         """
36         if not self.data[v1][v2]:
37             self.data[v1][v2] = 1
38             self.data[v2][v1] = 1
39             self.E += 1
40 
41     def has_edge(self, v1, v2):
42         """
43         判断是否有v1到v2的边
44         :param v1: 顶点
45         :param v2: 顶点
46         :return:
47         """
48         return self.data[v1][v2] == 1
49 
50     def print(self):
51         """
52         将图打印出来
53         :return:
54         """
55         for i in self.data:
56             print(i)

2.邻接表表示法

　　用邻接矩阵表示也有一定缺点，因为图的邻接矩阵经常是稀疏的，即图中大部分元素表示的都是无边的值，为了降低图表示的空间代价，可以使用邻接表表示法。

　　所谓邻接表，就是为图中每个顶点关联一个表，其中记录的是这个顶点的所有邻接边。顶点是图中最基本的部分，通常有标识，也可以顺序编号，以便可以通过编号随机访问。

　　要用邻接表来表示图，这里可以继承前面的类 Graph，需要对初始化方法、增加边等方法进行修改，具体代码如下：

 1 # 使用邻接表
 2 class GraphAL(Graph):
 3     def __init__(self, v):
 4         super(GraphAL, self).__init__(v)
 5         self.V = v
 6         self.E = 0
 7         self.data = [[] for _ in range(v)]
 8 
 9     def add_edge(self, v1, v2):
10         """
11         向图中增加一条v1到v2的边
12         :param v1: 顶点
13         :param v2: 顶点
14         :return:
15         """
16         if v2 not in self.data[v1]:
17             self.data[v1].append(v2)
18             self.data[v2].append(v1)
19             self.E += 1
20 
21     def has_edge(self, v1, v2):
22         """
23         判断是否有v1到v2的边
24         :param v1: 顶点
25         :param v2: 顶点
26         :return:
27         """
28         return v2 in self.data[v1]

 

三、图的遍历

1.深度优先搜索

　　按照深度优先搜索（Depth-First Search）的方法遍历整个图，假设从顶点 v 出发进行搜索，深度优先搜索的做法是：

• 访问顶点 v，并将其标记为已经访问过。
• 检查顶点 v 的邻接点，并从中取出一个尚未访问的顶点，从它出发继续进行深度优先搜索（递归），若不存在这种邻接点，则回溯。
• 反复进行上述操作直至从顶点 v 出发可以到达的顶点都已经访问过。
• 如果图中还存在尚未访问过的顶点，则从中选出一个顶点，重复进行上述过程，直至图中的所有顶点都已访问过。

2.广度优先搜索

　　按照广度优先搜索（Breadth-First Search）的方法遍历整个图，假设从顶点 v 出发进行搜索，广度优先搜索的做法是：

• 访问顶点 v，并将其标记为已经访问过。
• 依次访问顶点 v 的所有邻接点，再对每个邻接点的所有邻接点依次进行访问，直至所有的可到达的顶点都被访问过。
• 如果图中还存在尚未访问过的顶点，则从中选出一个顶点，重复进行上述过程，直至图中的所有顶点都已访问过。

3.深度优先搜索的实现

　　前面已经说过，深度优先搜索中包含了一个重复调用的过程，因而可以使用递归来实现深度优先搜索对图进行遍历。

　　在遍历的过程中，需要对已经访问过的顶点进行标记，所以定义了一个列表 visited，访问过的顶点就置为 True。除此之外，还要对访问的顶点进行记录，可以用一个列表来保存，定义为 path。具体代码如下：

 1 def graph_dfs(graph: GraphAL, s: int):
 2     """
 3     运用深度优先搜索对图进行遍历
 4     :param graph: 图
 5     :param s: 起点
 6     :return:
 7     """
 8     global visited, path, start
 9     visited = [False] * graph.get_vertex()
10     path = [0] * graph.get_vertex()
11     start = s
12     dfs(graph, s)
13 
14 
15 def dfs(graph: GraphAL, v: int):
16     """
17     深度优先搜索
18     :param graph: 图
19     :param v: 顶点
20     :return:
21     """
22     visited[v] = True
23     for i in graph.get_adj(v):
24         if not visited[i]:
25             path[i] = v
26             dfs(graph, i)

4.广度优先搜索的实现

　　在使用广度优先搜索对图进行遍历的过程中，需要使用到队列，首先将起点入队，当队列非空时，重复执行以下过程：

• 从队列中随机取出一个顶点。
• 对该顶点的所有邻接点进行遍历，若没有访问过，则加入到路径列表 path 中并标记为访问过。

　　当队列为空时，表明搜索完成，结束遍历。具体代码如下：

 1 def graph_bfs(graph: GraphAL, s: int):
 2     """
 3     运用广度优先搜索对图进行遍历
 4     :param graph: 图
 5     :param s: 起点
 6     :return:
 7     """
 8     global visited, path, start
 9     visited = [False] * graph.get_vertex()
10     path = [0] * graph.get_vertex()
11     start = s
12     bfs(graph, s)
13 
14 
15 def bfs(graph: GraphAL, v: int):
16     """
17     广度优先搜索
18     :param graph: 图
19     :param v: 顶点
20     :return:
21     """
22     visited[v] = True
23     q = Queue()
24     q.put(v)
25     while not q.empty():
26         v = q.get()
27         for node in graph.get_adj(v):
28             if not visited[node]:
29                 path[node] = v
30                 visited[node] = True
31                 q.put(node)

5.示例

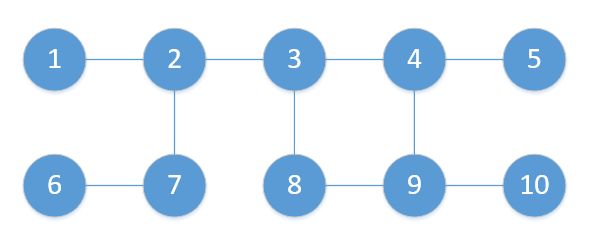
　　创建一个无向图 G，如下：

　　

　　使用邻接表来表示这个图，调用之前定义的图类 GraphAL，再将每条边依次添加进去，代码如下：

 1 graph_test = GraphAL(10)
 2 graph_test.add_edge(0, 1)
 3 graph_test.add_edge(1, 2)
 4 graph_test.add_edge(1, 6)
 5 graph_test.add_edge(2, 3)
 6 graph_test.add_edge(2, 7)
 7 graph_test.add_edge(3, 4)
 8 graph_test.add_edge(3, 8)
 9 graph_test.add_edge(5, 6)
10 graph_test.add_edge(7, 8)
11 graph_test.add_edge(8, 9)
12 graph_test.print()

　　前面搜索过程结束之后，路径都保存在了列表 path 之中，若我们想要获取从起点到目标顶点的路径，就需要从 path 中进行获取，获取路径的方法的代码如下：

 1 def get_path_to(v: int):
 2     """
 3     获取从顶点start到顶点v的路径
 4     :param v: 目标顶点
 5     :return:
 6     """
 7     x = path[v]
 8     result = [v, x]
 9     while x != start:
10         x = path[x]
11         result.append(x)
12     print(result[::-1])

　　最后就是分别使用深度优先搜索和广度优先搜索对图进行遍历，起点为顶点1，目标顶点为顶点8，最终分别使用 get_path_to() 获取路径，代码如下：

1 visited = []
2 path = []
3 start = None
4 graph_dfs(graph_test, 0)
5 get_path_to(7)
6 # [0, 1, 2, 3, 8, 7]
7 graph_bfs(graph_test, 0)
8 get_path_to(7)
9 # [0, 1, 2, 7]