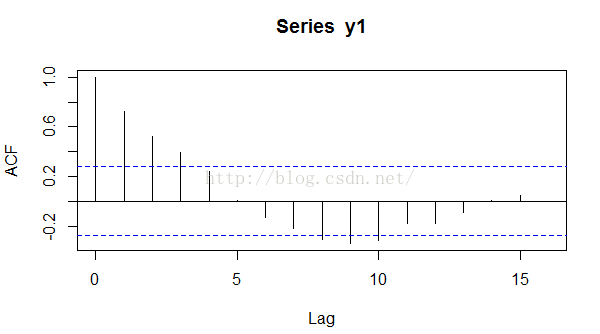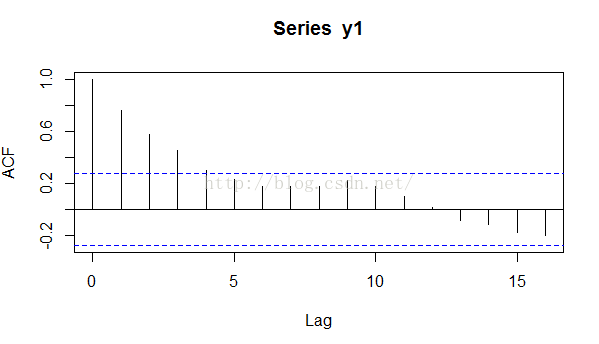时间序列分析这件小事（四）--AR模型

 无意中发现了一个巨牛的人工智能教程，忍不住分享一下给大家。教程不仅是零基础，通俗易懂，而且非常风趣幽默，像看小说一样！觉得太牛了，所以分享给大家。教程链接：https://www.cbedai.net/qtlyx

 

 

1.自回归

之前说了，分析时间序列和回归一样，目的都是预测。在回归里面，我们有一元回归于多元回归，在时间序列里面，我们有自回归。与一元、多元一样，我们分为一阶与多阶自回归。其实还是那样的理念，只不过之前是变量与应变量，现在则是存在时滞的序列之间的关系而已。

先来看一下一阶自回归AR(1)，也就是，Yt=b*Yt-1+ut。

在一开始我们就讨论了时间序列平稳性的重要程度，那么由这样一个一阶自回归形成的时间序列是否满足平稳性呢？答案是当自回归系数的绝对值小于1的时候，这样的一阶自回归序列是平稳的。

下面，我们就来构造一个满足一阶自回归的时间序列吧。

2.一阶自回归序列生产

我们来生成一个时间序列，其自回归方程如下：

yt = 0.8 * yt-1 + c

其中c是残差项，我们用白噪音，也就是正态分布来表示。具体的R代码如下：

 

#example 5
set.seed(1234)#设置随机种子
n = 50#序列数量
y1 = rep(0,n);#初始化y1时间序列
for(t in 2:n){#根据自回归方程计算y1序列
  y1[t] = 0.8*y1[t-1] + rnorm(1)
}
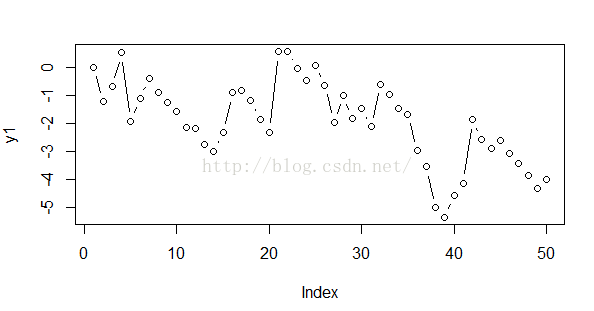
plot(y1,type = 'o')#绘制序列图

我们其实还可以使用R语言内置的函数快速完成回归序列的生成：

 

 

#example 6
y1  = arima.sim(n = 50,list(ar = 0.8))#R中自带函数，list中为各阶的自回归系数，由于我们只有一阶自回归，所以只有一个0.8
plot(y1,type = 'o')

 

 

 

 

 

 

 

然后我们看一下其自相关系数的图，很简单，和之前一样，acf(y1)即可。我们得到如下的自相关图。

这里我们可以看出，一阶自相关系数还是比较大的，与我们的模型0.8还算比价接近。如果我们给出的数据更加多的话，这一数值将会更加接近。在这里笔者补充一点，就是上面图中的蓝色虚线的作用。通常，我们认为超过蓝色虚线的自回归系数是显著的，也就是说如果我们做显著性检验的话，往往是能通过的，而没有超过蓝色虚线的那些回归系数，通常是不显著的。

3.AR模型估计

上面我们是自己建立了一个时间序列，那么如果我们现在只有一串时间序列，我们怎么去估计它的模型呢？换句话说，怎么去获得它的自回归方程呢？当然我们可以根据acf函数获得每一个lag的回归系数，然后就获得了一个多阶自回归模型，但是这样并不科学，我们有更加实际的方法。

其实，AR模型估计，说白了，就是线性回归求系数的过程。在线性回归中，我们用的是最小二乘法，在时间序列的AR模型中，我们介绍两种，yulr-walker与ols（即最小二乘法）

 

#example 7
ar(y1,method = "yule-walker")
ar(y1,method = "ols")

我们能在R中看到如下结果：

 

 

我们可以看到这些方法会告诉我们，那些阶数可以选择，自回归系数是多少。

这里，我们要知道，ols方法的精度不高，尽可能还是使用前者。

4.一个用R自带函数的demo

其实，我们上面的这一切，R语言都弄好了，很短的代码就可以实现。我们用一个2阶自回归模型作为例子来演示一下。

模型：yt = 0.7 * yt-1 - 0.5 yt-2 + c

同样的，c是误差项。

 

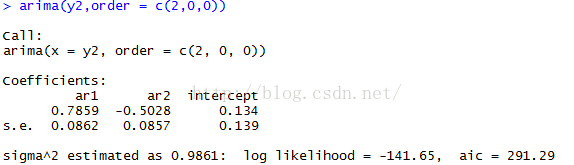
y2 = arima.sim(n = 100,list(ar = c(0.7,-0.5)))
plot(y2,type = 'o')
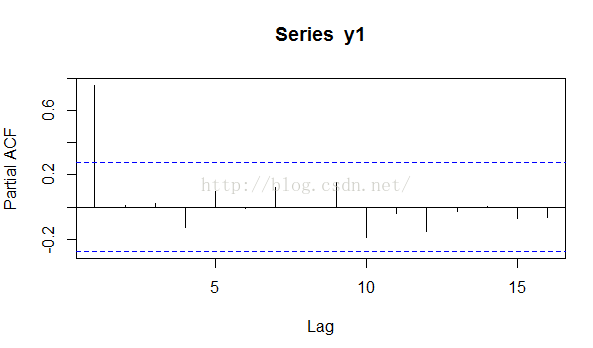
pacf(y2)$ac[1:5]

我们可以看到时间序列及其自回归系数。

 

 

这里，我们要区别acf与pacf函数，后者用于多阶的AR，而且第一个直线就是代表一阶滞后的相关系数，而与acf不同，第一个直线代表的是自己与自己的相关系数，当然就是1.当然啦，这只是表面的区别，深入的区别见后面第5部分。

然后我们用R中自带的模型估计函数来估计模型。

 

arima(y2,order = c(2,0,0))

这样，我们就能看到自回归系数了。如果我们在函数中加入include.mean = F，那么就不会有均值项，也就是显示中的intercept项。

 

5.acf与pacf

前面提到了一些acf与pacf的区别。其实学过微积分的人都是到偏导数，这里是类似的概念。

我们用acf的时候，会发现，对于一阶的AR模型，二阶滞后序列与原始序列的相关性也挺大的，原因就是yt-2与yt的相关性是由于yt-2与yt-1的相关性间接导致的，我们用acf的时候就没有考虑这一点，而用pacf的时候，则是消除了yt-1对yt-2的间接影响之后来计算yt与yt-2之间的相关性的了。

对比一下就一目了然了。

 

acf(y1)
pacf(y1)

 

acf的：

 

 

pacf：