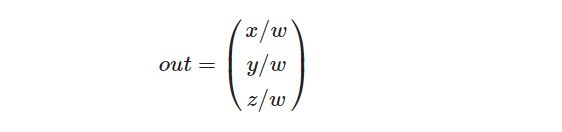坐标系统
opengl-坐标系统
- 概述
- 局部空间
- 世界空间
- 观察空间
- 裁剪空间
- 投影
- 正射投影
- 透视投影
- 组合
- Z缓冲
- 练习
研究坐标系,把握住以下三点:1、原点;2、坐标轴正方向;3、坐标单位
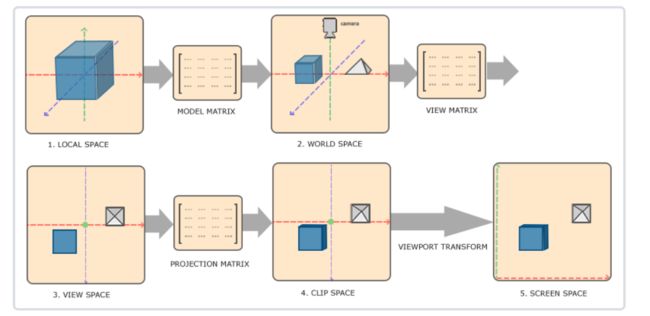
物体的 顶点 在最终转化为 屏幕坐标 之前还会被变换到多个坐标系统(Coordinate System)。
将物体的坐标变换到几个 过渡坐标系(Intermediate Coordinate System) 的优点在于,在这些特定的坐标系统中,一些操作或运算更加方便和容易
- 局部空间(Local Space,或者称为物体空间(Object Space))
- 世界空间(World Space)
- 观察空间(View Space,或者称为视觉空间(Eye Space))
- 裁剪空间(Clip Space)
- 屏幕空间(Screen Space)
概述
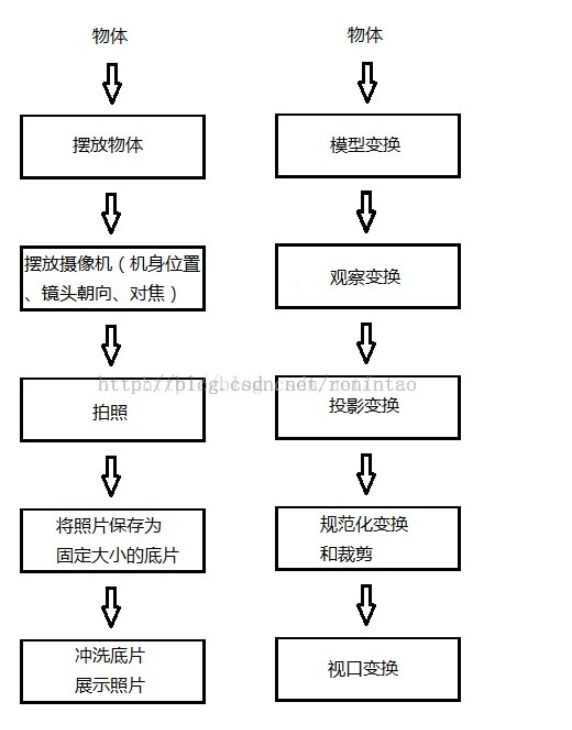
将坐标从一个坐标系变换到另一个坐标系,需要用到几个变换矩阵
最重要的几个分别是 模型(Model)、观察(View)、投影(Projection) 三个矩阵( MVP )
- 局部坐标是对象相对于局部原点的坐标,也是物体起始的坐标。
- 下一步是将局部坐标变换为世界空间坐标,世界空间坐标是处于一个更大的空间范围的。这些坐标相对于世界的全局原点,它们会和其它物体一起相对于世界的原点进行摆放。
- 接下来我们将世界坐标变换为观察空间坐标,使得每个坐标都是从摄像机或者说观察者的角度进行观察的。
- 坐标到达观察空间之后,我们需要将其投影到裁剪坐标。裁剪坐标会被处理至-1.0到1.0的范围内,并判断哪些顶点将会出现在屏幕上。
- 最后,我们将裁剪坐标变换为屏幕坐标,我们将使用一个叫做视口变换(Viewport Transform)的过程。视口变换将位于-1.0到1.0范围的坐标变换到由glViewport函数所定义的坐标范围内。最后变换出来的坐标将会送到光栅器,将其转化为片段。
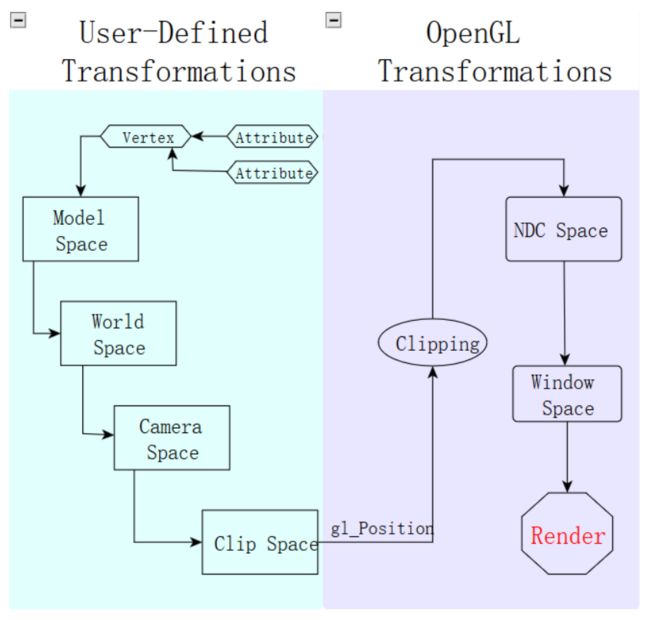
注意,OpenGL只定义了裁剪坐标系、规范化设备坐标系和屏幕坐标系,而局部坐标系(模型坐标系)、世界坐标系和照相机坐标系都是为了方便用户设计而自定义的坐标系
局部空间
局部空间是指物体所在的坐标空间,即对象最开始所在的地方
模型的所有顶点都是在局部空间中:它们相对于你的物体来说都是局部的
世界空间
世界空间中的坐标正如其名:是指顶点相对于(游戏)世界的坐标.
物体的坐标将会从局部变换到世界空间;该变换是由模型矩阵(Model Matrix)实现的.
在OpenGL中,世界坐标系是以 屏幕中心 为原点(0, 0, 0),且是始终不变的。你面对屏幕,你的右边是x正轴,上面是y正轴,屏幕指向你的为z正轴
右手坐标系
观察空间
观察空间经常被人们称之 OpenGL的摄像机(Camera) (所以有时也称为 摄像机空间(Camera Space) 或 视觉空间(Eye Space) )
观察空间是将世界空间坐标转化为用户视野前方的坐标而产生的结果。因此观察空间就是从摄像机的视角所观察到的空间
通过OpenGL中相机,改变视角,例如要观察-z轴方向的一个立方体的右侧面,可以有两种方式:
立方体不动,让相机绕着+y轴,旋转+90度,此时相机镜头朝向立方体的右侧面,实现目的。
相机不动,让立方体绕着+y轴,旋转-90度,此时也能实现同样的目的。注意这时相机没有转动。
OpenGL中采用方式2的观点来解释视变换
裁剪空间
在一个顶点着色器运行的最后,OpenGL期望所有的坐标都能落在一个特定的范围内,且任何在这个范围之外的点都应该被裁剪掉(Clipped)。被裁剪掉的坐标就会被忽略,所以剩下的坐标就将变为屏幕上可见的片段。这也就是 裁剪空间(Clip Space) 名字的由来。
所有顶点都为 标准化设备坐标(Normalized Device Coordinate, NDC) 。也就是说,每个顶点的x,y,z坐标都应该在-1.0到1.0之间,超出这个坐标范围的顶点都将不可见
为了将顶点坐标从观察空间变换到裁剪空间,我们需要定义一个 投影矩阵(Projection Matrix) ,它指定了一个范围的坐标,比如在每个维度上的-1000到1000。投影矩阵接着会将在这个指定的范围内的坐标变换为标准化设备坐标的范围(-1.0, 1.0)。所有在范围外的坐标不会被映射到在-1.0到1.0的范围之间,所以会被裁剪掉。在上面这个投影矩阵所指定的范围内,坐标(1250, 500, 750)将是不可见的,这是由于它的x坐标超出了范围,它被转化为一个大于1.0的标准化设备坐标,所以被裁剪掉了。
投影
正射投影
正射投影矩阵定义了一个类似立方体的 平截头箱,它定义了一个裁剪空间,在这空间之外的顶点都会被裁剪掉。创建一个正射投影矩阵需要指定可见平截头体的宽、高和长度。在使用正射投影矩阵变换至裁剪空间之后处于这个平截头体内的所有坐标将不会被裁剪掉。
glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);
前两个参数指定了平截头体的 左右坐标,第三和第四参数指定了平截头体的 底部和顶部。通过这四个参数我们定义了近平面和远平面的大小,然后第五和第六个参数则定义了 近平面和远平面的距离
透视投影
透视 : 离你越远的东西看起来更小,越近越大
透视投影矩阵 : 模拟透视的效果
投影矩阵将给定的 平截头体范围映射到裁剪空间,除此之外还 修改 了每个顶点坐标的 w 值,从而使得离观察者越远的顶点坐标w分量越大.被变换到裁剪空间的坐标都会在-w到w的范围之间(任何大于这个范围的坐标都会被裁剪掉)
OpenGL要求所有 可见的坐标 都落在 -1.0到1.0 范围内,作为顶点着色器最后的输出,因此,一旦坐标在裁剪空间内之后,透视除法就会被应用到裁剪空间坐标上
顶点坐标的每个分量都会除以它的w分量,距离观察者 越远顶点坐标就会越小。这是也是w分量非常重要的另一个原因,它能够帮助我们进行透视投影。最后的结果坐标就是处于标准化设备空间中的
正射投影矩阵和透视投影矩阵是如何计算:
http://www.songho.ca/opengl/gl_projectionmatrix.html
https://blog.csdn.net/zhanghua1816/article/details/23121735
glm::mat4 proj = glm::perspective(glm::radians(45.0f), (float)width/(float)height, 0.1f, 100.0f);
第一个参数定义了fov的值,它表示的是 视野(Field of View) ,并且设置了观察空间的大小。如果想要一个真实的观察效果,它的值通常设置为45.0,第二个参数设置了宽高比,由 视口的宽除以高 所得。第三和第四个参数设置了平截头体的 近和远平面 。我们通常设置近距离为0.1f,而远距离设为100.0f。所有在近平面和远平面内且处于平截头体内的顶点都会被渲染
屏幕宽高比 是一个必要的参数,因为我们要在一个宽高相等的单位化的盒子内展示所有的坐标系,而通常屏幕的宽度是大于屏幕的高度的,所以需要在水平方向上的轴线上布置更加密集的坐标点,竖直方向上相对稀疏。这样经过变换,我们就可以在保证看到更宽阔屏幕图像的需求下,根据X轴在单位盒子空间内的比例,在X方向上添加更多的X坐标
组合
Z缓冲
OpenGL存储深度信息在一个叫做Z缓冲(Z-buffer)的缓冲中,它允许OpenGL决定何时覆盖一个像素而何时不覆盖。通过使用Z缓冲,我们可以配置OpenGL来进行深度测试
glEnable(GL_DEPTH_TEST);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
练习
- 对GLM的projection函数中的FoV和aspect-ratio参数进行实验。看能否搞懂它们是如何影响透视平截头体的。
- 将观察矩阵在各个方向上进行位移,来看看场景是如何改变的。注意把观察矩阵当成摄像机对象。
- 使用模型矩阵只让是3倍数的箱子旋转(以及第1个箱子),而让剩下的箱子保持静止