Python求离散序列导数
有一组4096长度的数据,需要找到一阶导数从正到负的点,和三阶导数从负到正的点,截取了一小段。
394.0
388.0
389.0
388.0
388.0
392.0
393.0
395.0
395.0
394.0
394.0
390.0
392.0
按照之前所了解的,对离散值求导其实就是求差分,例如第i点的导数(差分)为:
y(s)i=C−myi−m+C−m+1yi−m−1+...+Cm−1yi+m−1+Cmyi+m
即在一个宽度为2m+1的窗口内通过计算前后m个值加权后的和得到。但是在实际使用过程中效果不是很好。于是想到了同样在一个宽度为2k+1的窗口内,将这2k+1个点拟合成一个函数,然后求导就可以得到任意阶数的导数值。
首先是函数拟合,使用from scipy.optimize import leastsq即最小二乘拟合
from scipy.optimize import leastsq
class search(object):
def __init__(self, filename):
self.filename = filename
def func(self, x, p):
f = np.poly1d(p)
return f(x)
def residuals(self, p, x, y, reg):
regularization = 0.1 # 正则化系数lambda
ret = y - self.func(x, p)
if reg == 1:
ret = np.append(ret, np.sqrt(regularization) * p)
return ret
def LeastSquare(self, data, k=100, order=4, reg=1, show=1): # k为求导窗口宽度,order为多项式阶数,reg为是否正则化
l = self.len
step = 2 * k + 1
p = [1] * order
for i in range(0, l, step):
if i + step < l:
y = data[i:i + step]
x = np.arange(i, i + step)
else:
y = data[i:]
x = np.arange(i, l)
try:
r = leastsq(self.residuals, p, args=(x, y, reg))
except:
print("Error - curve_fit failed")
fun = np.poly1d(r[0]) # 返回拟合方程系数
df_1 = np.poly1d.deriv(fun) # 求得导函数
df_2 = np.poly1d.deriv(df_1)
df_3 = np.poly1d.deriv(df_2)
df_value = df_1(x)
df3_value = df_3(x)fun = np.poly1d(r[0]),fun返回的是一个 polynomial class,具体使用可以见官方文档numpy.poly1d
polynomial对象可以使用deriv方法求导数,求得的依然是 polynomial对象。 df_value = df_1(x)所得到的就是x这个几个点求得的导数值。
看似大功告成,但是求导的结果并不是很好,如下图,实际最高点在100左右,但是拟合出来的曲线最高点在120左右,而原因在于使用多项式拟合很难准确拟合曲线。
于是想用高斯函数来实现对曲线的拟合,在matlab中试了下,三阶高斯拟合可以很好的拟合曲线,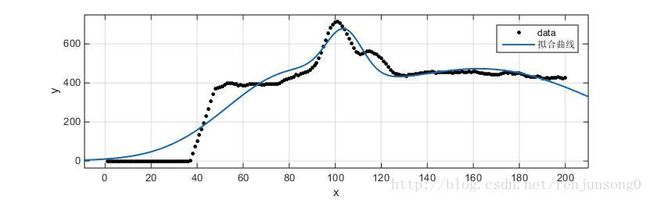
但是numpy以及sicpy中没有找到类似poly1d这种对象,虽然可以自己定义高斯函数,如下
def gaussian(self, x, *param):
fun = param[0]*np.exp(-np.power(x - param[2], 2.) / (2 * np.power(param[4], 2.)))+param[1]*np.exp(-np.power(x - param[3], 2.) / (2 * np.power(param[5], 2.)))
return fun但是,在通过最小二乘拟合得到函数参数后只能得到拟合后的点,无法直接求导数..所以并不适合。
所以还是只能回到多项式拟合,如果4阶多项式不能表征的话,更高阶的呢
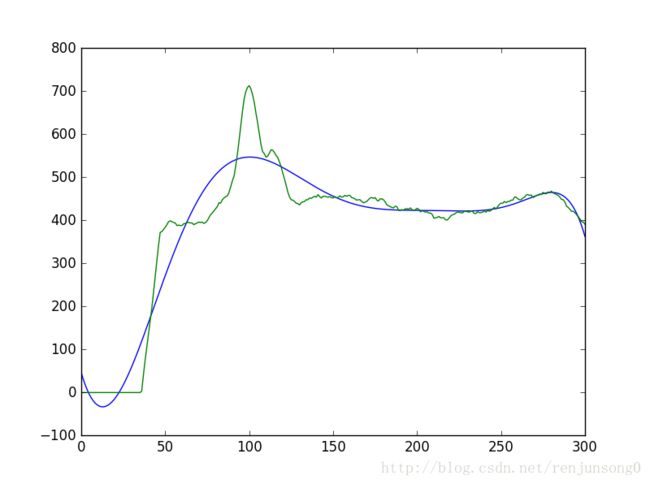
总体来说,效果还是可以接受的。
如果下阶段找到好的高斯函数拟合方法,会继续更新。
