深度学习第二章:神经网络的原理和实现
声明:此博客为个人笔记。参考书籍详见https://www.ituring.com.cn/book/1921
文章目录
- 一、前言
- 二、什么是神经网络
- 2、1神经网络的结构
- 2、2神经网络的工作流程
- 三、理解激活函数
- 3.1什么是激活函数
- 3.2激活函数的种类
- 3.2.1阶跃函数
- 3.2.2 sigmoid函数
- 3.2.3 ReLU函数
- 四、神经网络的实现
- 4.1符号确认
- 4.2各层信号传递的实现
- 4.3代码实现
- 五、输出层的设计
- 5.1恒等函数
- 5.2 softmax函数
一、前言
神经网络和感知机的关系:感知机是神经网络的基础。对于复杂的函数,感知机也隐含着能够表示它的可能性。但是,在感知机中,如何确定合适的、能符合预期的输入与输出的权重,还是由人工进行的。
神经网络的出现就是为了解决上述问题。
二、什么是神经网络
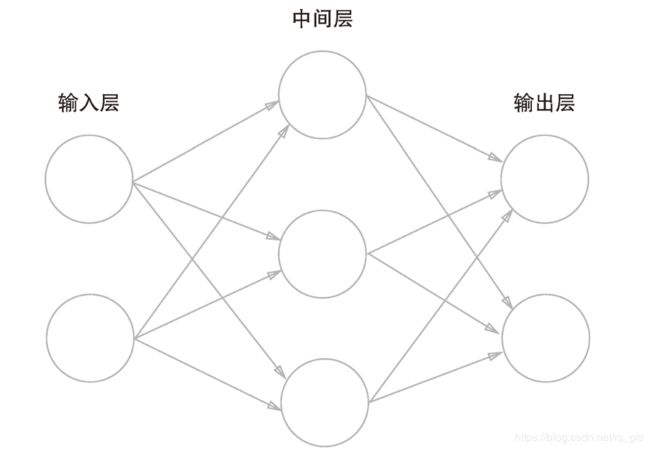
2、1神经网络的结构
2、2神经网络的工作流程
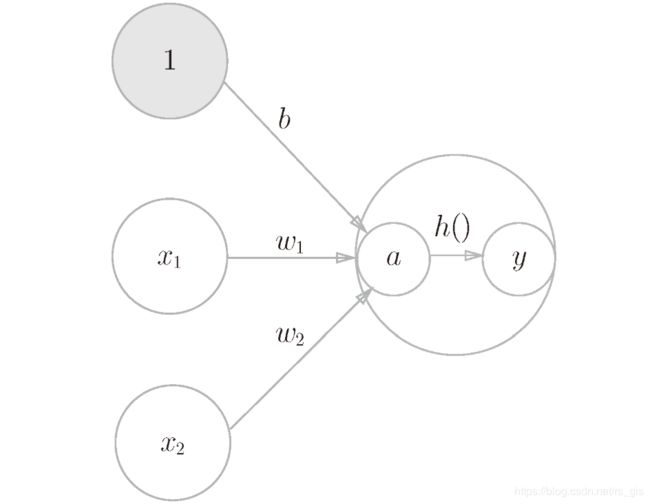
神经网络的工作流程:输入层:输入x1、x2、偏置b(此处取1);隐藏层:输入层和各自的权重相乘后得到一个新的值a(a=b + w1 * x1 + w2 *x2)传送至下一个神经元(即隐藏层),在隐藏层中有激活函数 h(),h(a)=y,输出层:y。
注:输出层有可以作为下一层的输出层。
三、理解激活函数
3.1什么是激活函数
激活函数:将输入信号的和转换为输出信号的函数称为激活函数。
激活函数的作用在于决定如何来激活输入信号的总和。
注意:单层感知机(朴素感知机)使用的是阶跃函数(阶跃函数是一但超过阈值就切换输出的函数)。多层感知机(神经网络)则使用平滑的激活函数。
事实上,将激活函数从阶跃函数换成其他函数,就可以进入到神经网络的世界中了。 即感知机和神经网络的区别在于激活函数!
3.2激活函数的种类
函数可分为线性函数和非线性函数。但是神经网络的激活函数只能是非线性激活函数。即线性激活函数不嫩作为神经网络的激活函数
原因:
对于激活函数:h(x)=cx
如果h()为线性: y(x)=h( h ( h(x) ) )
则:y(x)= c * c * c * x
如此,多加的层就无任何意义(可一直接用一层表示)
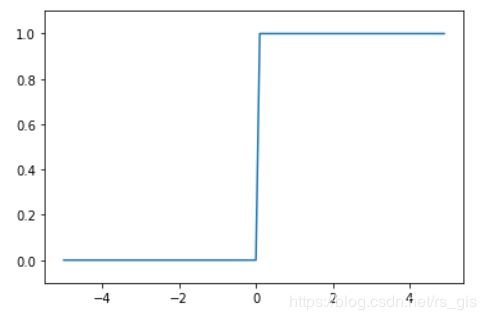
3.2.1阶跃函数
阶跃函数:当输入超过0是,输出1;否则输出0
import numpy as np
import matplotlib.pylab as plt
#定义阶跃函数
def step_function(x):
return np.array(x>0)
#显示图形
x = np.arange(-5.0,5.0,0.1) #输入的x的范围
y = step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1) #设置y轴范围
plt.show()
3.2.2 sigmoid函数
神经网络中最常使用的一个函数就是sigmoid函数
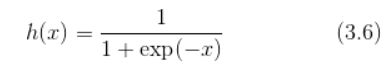
sigmoid函数实现:
import numpy as np
import matplotlib.pylab as plt
def sigmoid_function(x):
y = 1/(1+np.exp(-x))
return y
x = np.arange(-5.0,5.0,0.1) #输入的x的范围
y = sigmoid_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1) #设置y轴范围
plt.show()
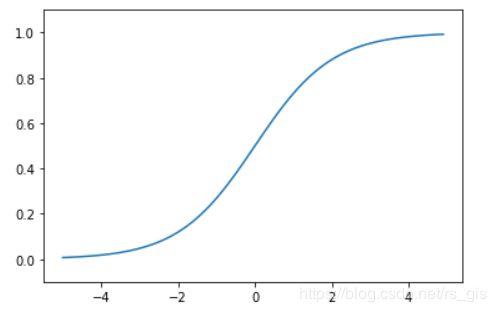
阶跃函数和sigmoid函数比较
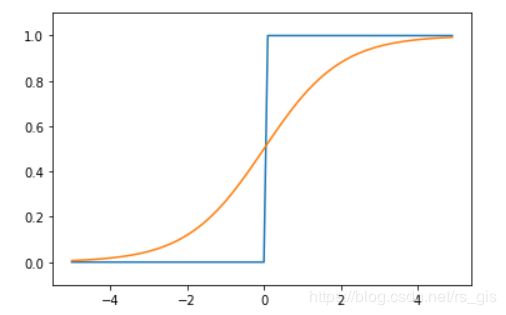
sigmoid函数的平滑性对神经网络的学习具有重要意义。输入信号不管有多小或者多大,输出信号都在0到1之间。
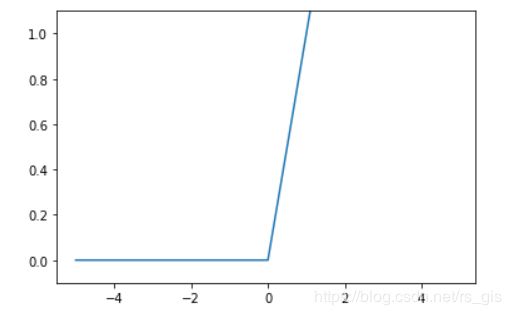
3.2.3 ReLU函数
import numpy as np
import matplotlib.pylab as plt
def ReLU(x):
return np.maximum(0,x)
x = np.arange(-5.0,5.0,0.1) #输入的x的范围
y = ReLU(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1) #设置y轴范围
plt.show()
四、神经网络的实现
我们使用NumPy矩阵实现神经网络。(本节实现的神经网络的前向处理(foeward),后向处理(backword)会在后面介绍)
要实现的神经网络如下:
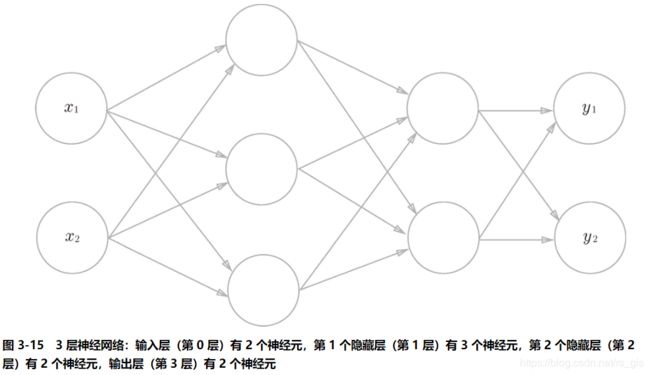
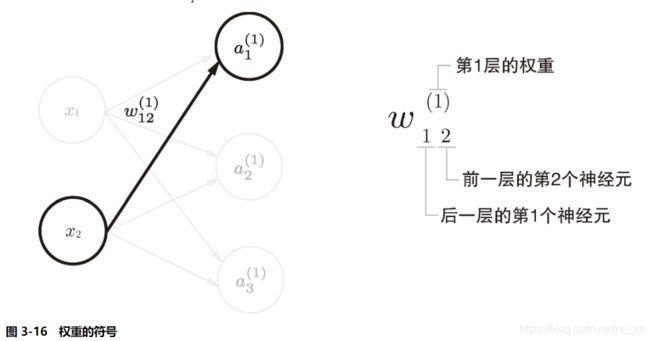
4.1符号确认
4.2各层信号传递的实现
1、从输入层到第1层的信号传递
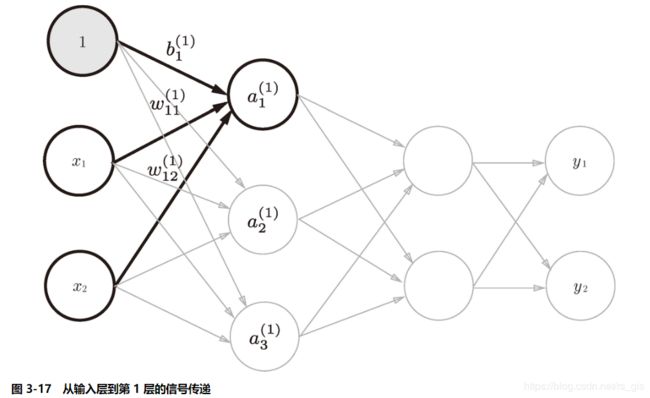
从输入层到第1层的激活函数实现过程
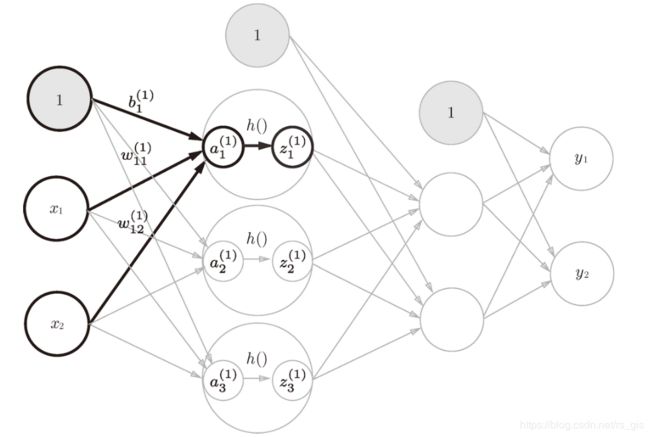
2、从第1层到第2层的信号传递
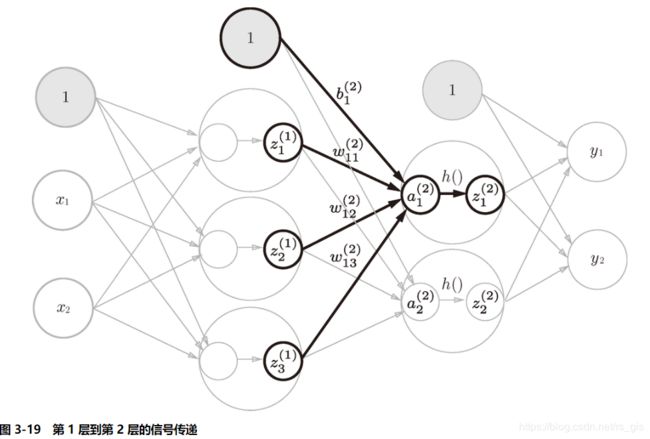
3、从第2层到输出层的信号传递
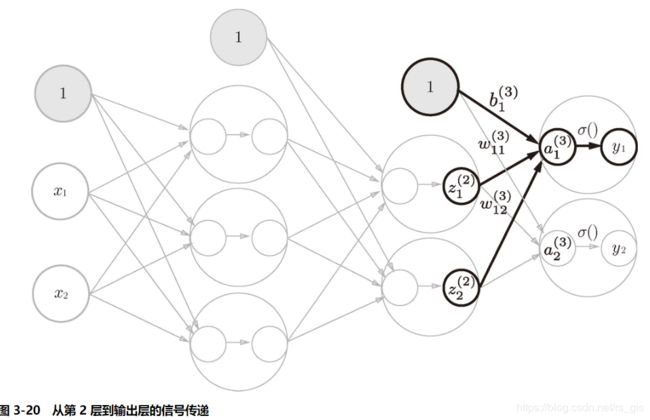
4.3代码实现
使用矩阵实现神经网络时,主要根据以下公式:
A = X * W + B
A、X、W、B都是矩阵
下面实现上述三层神经网络,上面三层神经网络包含3个权重(权重记为W,分别为W1,W2,W3),3个偏置(偏置记为b,b1,b2,b3);以及2个输入(输入记为x,分别记为x1,x2),2个输出(输出记为y,分别记为y1,y2)
import numpy as np
#定义函数,存储权重和偏置
def init_network():
network = {}
#第0层到第1层参数
network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['b1'] = np.array([0.1,0.2,2.3])
#第1层到第2层参数
network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network['b2'] = np.array([0.1,0.2])
#第2层到第3层参数
network['W3'] = np.array([[0.1,0.3],[0.2,0.4]])
network['b3'] = np.array([0.1,0.2])
return network
def sigmoid_function(x):
y = 1/(1+np.exp(-x))
return y
#实现前向传播过程
def forword(network,x):
W1,W2,W3 = network['W1'],network['W2'],network['W3']
b1,b2,b3 = network['b1'],network['b2'],network['b3']
#第1层
a1 = np.dot(x,W1)+b1
z1 = sigmoid_function(a1)
#第2层
a2 = np.dot(z1,W2)+b2
z2 = sigmoid_function(a2)
#第3层(输出层)
a3 = np.dot(z2,W3)+b3
y=sigmoid_function(a3)
return y
network = init_network()
x = np.array([1.0,0.5])
y = forword(network,x)
print(y)
结果:[0.57993256 0.67019281]
五、输出层的设计
神经网络可以用在分类问题和回归问题上,不过需要根据情况改变输出层的激活函数。一般而言,回归问题用恒等函数,分类问题用softmax函数
5.1恒等函数
恒等函数会将输入按原样输出,即对输入的信息,不加以任何改动地直接输出。
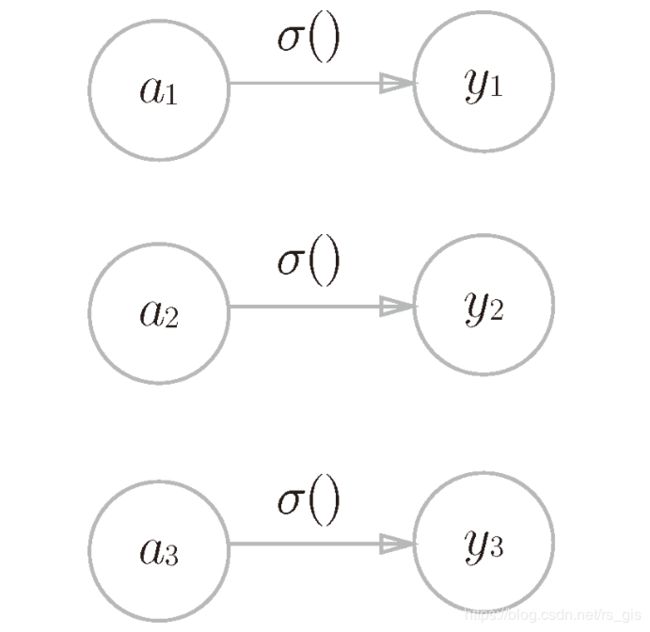
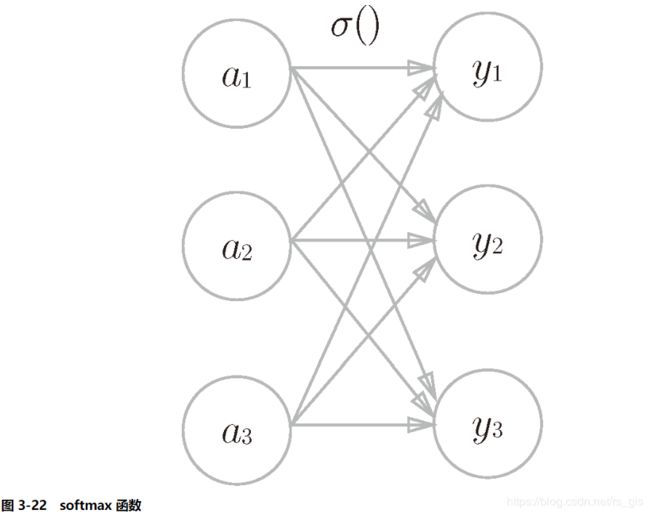
5.2 softmax函数
softmax实现如下:
import numpy as np
a = np.array([0.3,2.9,4.0])
def softmax(self):
exp_a = np.exp(a)
print('分子:',exp_a)
sum_exp_a = np.sum(exp_a)
print('分母:',sum_exp_a)
y_a = exp_a/sum_exp_a
return y_a
b = softmax(a)
print(b)
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) # 溢出对策
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
结果如下:
[0.01650685 0.24561748 0.73787568]
因为softmax函数的输出是0.0到1.0之间的实数,并且softmax函数的输出值的总和为1是softmax函数的一个重要性质。正因为有了这个性质,我们才可以吧softmax函数的输出解释为“概率”。
注意:softmax函数一般用在模型的学习阶段,在推理阶段softmax一般会省略。